趣味理解朴素贝叶斯
 0
0
 1837
1837
趣味理解朴素贝叶斯
NavieBayes
生活中很多场合需要用到分类,比如新闻分类、病人分类等等实际用用场景。为了让大家可以形象的理解,本文从实际的应用入手介绍一种简单的常用分类算法—-朴素贝叶斯(Navie Bayes classifier)。
- 01 病人分类的例子
让我从一个例子开始讲起,你会看到贝叶斯分类器很好懂,一点都不难。某个医院早上收了六个门诊病人,如下表。
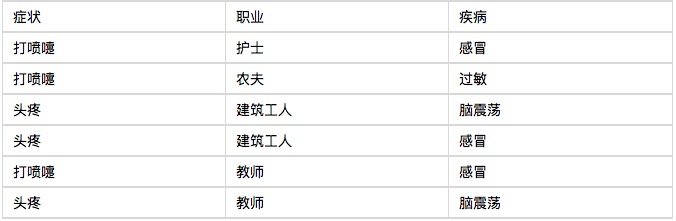
现在又来了第七个病人,是一个打喷嚏的建筑工人。请问他患上感冒的概率有多大? 根据贝叶斯定理:
P(A|B) = P(B|A) P(A) / P(B)
可得:
P(感冒|打喷嚏x建筑工人)
= P(打喷嚏x建筑工人|感冒) x P(感冒)
/ P(打喷嚏x建筑工人)
假定”打喷嚏”和”建筑工人”这两个特征是独立的,因此,上面的等式就变成了
P(感冒|打喷嚏x建筑工人)
= P(打喷嚏|感冒) x P(建筑工人|感冒) x P(感冒)
/ P(打喷嚏) x P(建筑工人)
这是可以计算的。
P(感冒|打喷嚏x建筑工人)
= 0.66 x 0.33 x 0.5 / 0.5 x 0.33
= 0.66
因此,这个打喷嚏的建筑工人,有66%的概率是得了感冒。同理,可以计算这个病人患上过敏或脑震荡的概率。比较这几个概率,就可以知道他最可能得什么病。
这就是贝叶斯分类器的基本方法:在统计资料的基础上,依据某些特征,计算各个类别的概率,从而实现分类。
- 02 朴素贝叶斯分类器的公式
假设某个体有n项特征(Feature),分别为F1、F2、…、Fn。现有m个类别(Category),分别为C1、C2、…、Cm。贝叶斯分类器就是计算出概率最大的那个分类,也就是求下面这个算式的最大值:
P(C|F1F2...Fn)
= P(F1F2...Fn|C)P(C) / P(F1F2...Fn)
由于 P(F1F2…Fn) 对于所有的类别都是相同的,可以省略,问题就变成了求
P(F1F2...Fn|C)P(C)
的最大值。
朴素贝叶斯分类器则是更进一步,假设所有特征都彼此独立,因此
P(F1F2...Fn|C)P(C)
= P(F1|C)P(F2|C) ... P(Fn|C)P(C)
上式等号右边的每一项,都可以从统计资料中得到,由此就可以计算出每个类别对应的概率,从而找出最大概率的那个类。
虽然”所有特征彼此独立”这个假设,在现实中不太可能成立,但是它可以大大简化计算,而且有研究表明对分类结果的准确性影响不大。
下面再通过两个例子,来看如何使用朴素贝叶斯分类器。
- 03 账号分类
根据某社区网站的抽样统计,该站10000个账号中有89%为真实账号(设为C0),11%为虚假账号(设为C1)。接下来,就要用统计资料判断一个账号的真实性。
C0 = 0.89 C1 = 0.11
假定某一个账号有以下三个特征 F1: 日志数量/注册天数 F2: 好友数量/注册天数 F3: 是否使用真实头像(真实头像为1,非真实头像为0) F1 = 0.1 F2 = 0.2 F3 = 0
请问该账号是真实账号还是虚假账号?方法是使用朴素贝叶斯分类器,计算下面这个计算式的值。
P(F1|C)P(F2|C)P(F3|C)P©
虽然上面这些值可以从统计资料得到,但是这里有一个问题:F1和F2是连续变量,不适宜按照某个特定值计算概率。一个技巧是将连续值变为离散值,计算区间的概率。比如将F1分解成[0, 0.05]、(0.05, 0.2)、[0.2, +∞]三个区间,然后计算每个区间的概率。在我们这个例子中,F1等于0.1,落在第二个区间,所以计算的时候,就使用第二个区间的发生概率。
根据统计资料,可得:
P(F1|C0) = 0.5, P(F1|C1) = 0.1 P(F2|C0) = 0.7, P(F2|C1) = 0.2 P(F3|C0) = 0.2, P(F3|C1) = 0.9
因此
P(F1|C0) P(F2|C0) P(F3|C0) P(C0) = 0.5 x 0.7 x 0.2 x 0.89 = 0.0623 P(F1|C1) P(F2|C1) P(F3|C1) P(C1) = 0.1 x 0.2 x 0.9 x 0.11 = 0.00198 可以看到,虽然这个用户没有使用真实头像,但是他是真实账号的概率,比虚假账号高出30多倍,因此判断这个账号为真。
- 04 性别分类
下面是一组人类身体特征的统计资料。
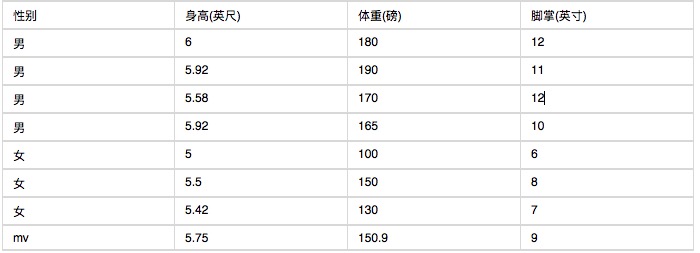
已知某人身高6英尺、体重130磅,脚掌8英寸,请问该人是男是女?根据朴素贝叶斯分类器,计算下面这个式子的值。
P(身高|性别) x P(体重|性别) x P(脚掌|性别) x P(性别)
这里的困难在于,由于身高、体重、脚掌都是连续变量,不能采用离散变量的方法计算概率。而且由于样本太少,所以也无法分成区间计算。怎么办?这时,可以假设男性和女性的身高、体重、脚掌都是正态分布,通过样本计算出均值和方差,也就是得到正态分布的密度函数。有了密度函数,就可以把值代入,算出某一点的密度函数的值。比如,男性的身高是均值5.855、方差0.035的正态分布。所以,男性的身高为6英尺的概率的相对值等于1.5789(大于1并没有关系,因为这里是密度函数的值,只用来反映各个值的相对可能性)。
有了这些数据以后,就可以计算性别的分类了。
P(身高=6|男) x P(体重=130|男) x P(脚掌=8|男) x P(男)
= 6.1984 x e-9
P(身高=6|女) x P(体重=130|女) x P(脚掌=8|女) x P(女)
= 5.3778 x e-4
可以看到,女性的概率比男性要高出将近10000倍,所以判断该人为女性。
转载自 阮一峰 的微信公众号
- 3.2 模板:数字货币交易类库 (集成 现货、 期货支持OKCoin期货/BitVC)
- 风险小史(六) 很抱歉,高斯就做了一点微小的工作
- 风险小史(四) 棣莫弗与神之曲线
- 风险小史(五) 贝叶斯,一个只活在教材里的男人
- 对于止损的另类而犀利的解释
- OkCoin中国站API错误代码查询
- 2.12 _D( ) 函数 与 时间戳
- python: 这些地方请你小心
- 协整的直观认识
- 隐马尔科夫模型
- 2.11 API: Chart 函数使用的简单例子(画图功能)
- 详解货币对
- 警惕线性思维陷阱
- 听说这样的阅读方式,能变现很多财富
- 在赌博与投资中 “逃命”与“活命”的故事
- 30行代码带你进入量化投资世界(python版本)
- 博弈,是一种高情商的体现
- 量价关系是一个重要的指标!
- 强烈要求平台添加做方面的回测功能
- 如何有料又有趣的读懂财务三大表?