版权声明：如需对此文章代码进行转载请注明出处，若用于商业用途、论文写作请私信或联系作者邮箱940648114@qq.com

一、前言

量化交易的优势之处

        量化交易是指以先进的数学模型替代人为的主观判断，利用计算机技术从庞大的历史数据中海选能带来超额收益的多种“大概率”事件以制定策略，极大地减少了投资者情绪波动的影响，避免在市场极度狂热或悲观的情况下作出非理性的投资决策。         由于数字货币24*7小时不间断的交易市场的连续性，并且量化交易可以达到高频交易的效果，从数字货币市场入手显然是做量化的很好的起步点。目前数字货币市场仍然是不成熟的。平台交易系统的宕机，k线插针依然是会偶尔出现，对于量化交易也是一种风险所在。不过对于数字货币进行量化交易总体来看依然是利大于弊。因为通过模型的回测训练和时间序列的回测分析，我们可以在最短时间能尝试到数百种模型中最合适的方式。

二、GQNR模型简介

        本模型是基于Garch模型预测波动率，通过分位数回归预测波动率的VaR值进而利用非线性回归，例如GA进行拟合来预测未来下一个周期中的上限VaR以及下限VaR，在后文中将这种方法模型简称为GQNR。

1.Garch模块

        本板块将会详细介绍策略Garch核心的推导，此方法在金融市场具有一定的普适性，在数字货币上能到达一定预测效果。

1.1Garch定义

        ARCH模型的实质是使用残差平方序列的q阶移动平移拟合当期异方差函数值，由于移动平均模型具有自相关系数q阶截尾性，所以ARCH模型实际上只适用于异方差函数短期自相关系数。         但是在实践中，有些残差序列的异方差函数是具有长期自关性，这时使用ARCH模型拟合异方差函数，将会产生很高的移动平均阶数，增加参数估计的难度并最终影响ARCH模型的拟合精度。         为了修正个问题，提出了广义自回归条件异方差模型， 这个模型简记为GARCH（p,q）.         GARCH模型实际上就是在ARCH的基础上，增加考虑异方差函数的p阶自回归性而形成，它可以有效的拟合具有长期记忆性的异方差函数。ARCH模型是GARCH模型的一个特例，p=0的GARCH（p,q）模型。

1.2ARCH过程

        定义σn是在第n-1个交易周期估计资产在第n个交易周期的波动率，mu为日收益率，那么可以根据最近m个交易周期的收益率进行无偏估计： $$ \sigma n^2= \frac{1}{m-1} \sum\limits{i=1}^m {( { \mu_{n-i}- \overline{\mu} } ) ^2}, $$         做以下变化①将μn-i换成百分比收益率；②将m-1换成m；③假设μ=0,并且这些变化对结果影响不大，根据上式可以将波动率简化为： $$ \sigma n^2= \frac{1}{m} \sum\limits{i=1}^m { \mu_{n-i} ^2}, $$         也就是说每一个周期的波动率的平方具有等权重1/m，由于是估计当前的波动率，距离近的数据应该赋予更高权重，则上式可以更改为： $$ \sigma n^2= \sum\limits{i=1}^m { \alpha_i\mu_{n-i} ^2}, $$         αi是第i个交易周期的收益率平方的系数，取正值且i越小值越大，权重之和为1。进一步推广，假定存在一个长期的方差率VL，且对应的权重为γ，根据上式可以得到：

$$ \begin{cases}\sigma n^2= \gamma V{L}+\sum\limits_{i=1}^m { \alpha_i\mu_{n-i} ^2}\ &\ \gamma+\sum\limits_{i=1}^m{\alpha_i\mu_{n-i}^2}=1 & \end{cases} , $$         令ω=γVL，公式(15)可以改写为： $$ \sigma n^2= \omega+\sum\limits{i=1}^m { \alpha_i\mu_{n-i} ^2}, $$         根据上式我们可以得到常见的ARCH(1)过程 $$ \sigma n^2= \omega+{ \alpha\mu{n-1} ^2}, $$

1.3GARCH过程

        GARCH(p,q)模型是ARCH§和EWMA(q)模型的结合，意义为波动率不仅与前p期收益有关，还与自身前q期有关，表达式如下： $$ \sigma n^2= \omega+\sum\limits{i=1}^m { \alpha_i\mu_{n-i} ^2}+\sum\limits_{i=1}^m { \beta_i\sigma_{n-i} ^2}, $$         根据上式我们可以得到常见的GARCH(1,1)： $$ \begin{cases}\sigma n^2= \omega+{ \alpha\mu{n-1} ^2+\beta\sigma_{n-1}^2}\&\ \qquad\alpha+\beta+\gamma=1 & \end{cases} , $$

2 QR模块

        本板块将会阐述基本的分位数回归，描述策略性分位数的重要性

2.1 QR定义

        分位数回归是估计一组回归变量X与被解释变量Y的分位数之间线性关系的建模方法。         以往的回归模型实际上是研究被解释变量的条件期望。而人们也关心解释变量与被解释变量分布的中位数，分位数呈何种关系。它最早由Koenker和Bassett(1978)提出。OLS回归估计量的计算是基于最小化残差平方。分位数回归估计量的计算也是基于一种非对称形式的绝对值残差最小化。其中，中位数回归运用的是最小绝对值离差估计(LAD，least absolute deviations estimator)。

2.2 由OLS到QR

        一般的回归方法是最小二乘法，即最小化误差的平方和： $$ min \sum{({y_i- \widehat{y}i })}^2 $$        而分位数的目标就是在上述公式基础上最小化加权的误差绝对值和： $$ \mathop{\arg\min\beta}\ \ \sum{[{\tau(y_i-X_i\beta)^++(1-\tau)(X_i\beta-y_i) ^+ }]} $$

2.2 QR可视化

       可以看到，所有样本被回归线分成了不同的空间，而这个回归线也就成了分位线

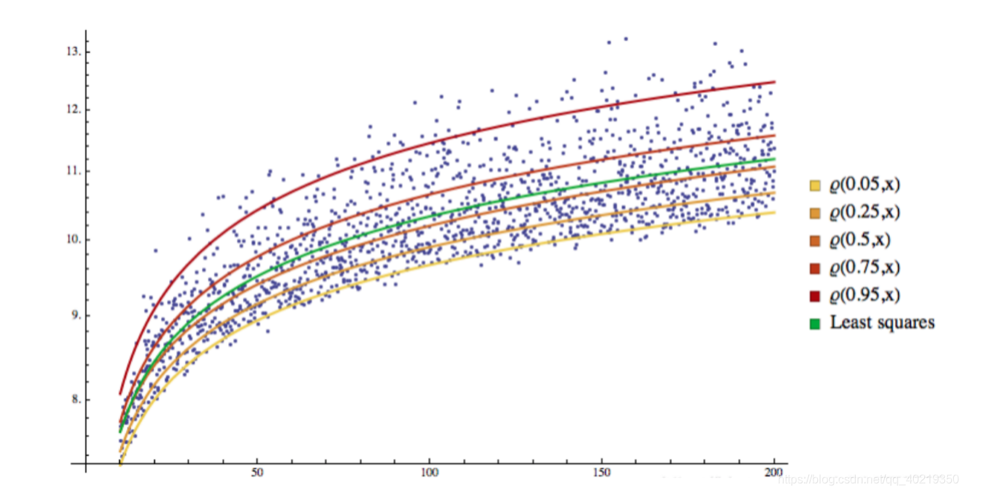
3.GARCH-QR回归

        我们很自然联想到，是否可以用市场未知的波动率sigma与分位数Q即VaR进行回归来预测未来大概率情况下波动阈值，本板块将进行这一方向的展开。

3.1 选定波动率与VaR的回归形式

        由于此处涉及策略核心，我暂且举一个形式，以说明思路。 $$ VaR=\epsilon+W^TE\E=(\zeta,\zeta^2,\zeta^3,\zeta^4)\W=(W_1,W_2,W_3,W_4) $$

3.2 确定目标函数

       根据以上信息，我们进行组合后可以得到最终待优化的目标函数： $$ \widehat{W}=\mathop{\arg\min_W}\ \ \sum{[{\alpha(VaR_t-W^TE_t)^++(1-\alpha)(W^TE_t-VaR_t) ^+ }]} $$

3.3 使用机器学习进行目标函数的优化

       本步骤可选性比较多，传统的梯度下降，也可以遗传算法，读者可以发挥自己的创意进行实验。本处采取的是优化后的GA算法，曾在另一篇自己的blog里面详细介绍过不再展开，有关于GA算法地址

三、如何在量化中运用GQNR

1.思路的确定

       GQNR的核心在于市场的波动率，在每一期当前的时间点上，可以通过GARCH预测出对于下一期波动率的预测，在另一方面，通过过往数据预测波动率的分位数回归，能够获得在大概率情况下不会超出的波动阈值上边界与下边界。而这两个边界，就是整体的核心。一旦触发上边界，我们可以认为在大概率下短期会有回调的趋势，一旦触发下边界，我们可以认为在大概率情况下短期会有拉升趋势。

2.运用的难点

• 采取回归的形式
• 适应性算法的选择
• 机器学习合适的参数
• 市场的不确定随机性

3.解决方案

• 减短策略学习的时间周期
• 降低单笔下仓保证金抵抗长期风险
• 增加双均线趋势共同验证以及二次阈值确认