韭菜与买卖价差——EKOP模型初探

韭菜与买卖价差——EKOP模型初探

• 1 前言

  最近异常忙碌，离上次写专栏已经过去数月。这几个月发生了许多事情，其中的一些对于我自己的人生来说，是不折不扣的黑天鹅。不过这些经历告诉我，生活与交易一样，起起落落，充满未知。我们总是希望能够从已经发生的事情中学习到一些东西，慢慢地去接近或许并不存在的真相。

  闲话少叙，入正题。我们都知道，一个交易活跃的股票通常有着比较小的买卖价差（spread），而一个交易不活跃的股票则相反。为什么会出现这样的情况呢？能否用一个简单漂亮的数学模型解释价差的差异？今天要谈的EKOP模型[1]在提出之初，就是为了研究拥有不同信息的交易者的行为，是否是造成这两类股票价差存在差异的原因。在这篇专栏文章中，我将介绍这个模型的基础。模型的应用，会在后续的文章中（如果我有时间写的话）做进一步分析。数学模型的简洁之美在这篇论文里展现的淋漓尽致，阅读论文的过程充满享受。

• 2 交易过程之假设

  当我们谈论一个金融模型，最重要的就是关注这个模型的假设。好的金融模型都有恰如其分的假设：它不会太强，以至于没有通用性；它也不会太弱，以至于推导不出漂亮简洁的结果。EKOP模型的基本假设有如下几条：

  假设1：我们讨论股票的交易，交易行为在日间离散、日内连续假设。这是说，交易者的交易行为发生在 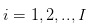这些离散的交易日中。而在交易日内，交易发生在 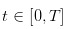这样的连续时间上。令 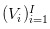为一组表示股票在每一天日末时股票价值的随机变量，每一天有三种可能的情况

  • 发生坏消息，我们将股票的价值记为
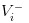
  • 发生好消息，我们将股票的价值记为
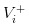
  • 没有消息发生，我们将股票的价值记为

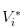
  很明显，我们有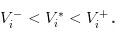

  假设2：在某一天，有α

  的概率发生影响股票价格的事件，则有1-α的概率不会发生影响股价的事件。在发生事件的那些天，又有δ的概率发生会让股价降低的坏事件，而有1-δ的概率发生会使股价上升的好事情。

  假设3：股票交易的参与者有做市商（market maker，简写作MM），知情交易者（informed trader，简写做IT），和不知情交易者（uninformed trader，简写做UT）.他们分别遵从这样的交易行为：

  MM是总是时刻准备着去挂一个单位的买单或卖单，尽作为一个做市商的义务。MM是风险中性的，因此他挂单的价格是他自己认为的公允价格。

  IT只在有消息发生的日子才交易，他们的交易行为是一个泊松过程。某一天，如果有坏消息发生，他就会以μ的到达率（arrival rate）挂一个卖单；而在发生好消息的那些天，他会以μ的到达率挂一个买单。

  UT，也就是我们可怜的韭菜，由于没有消息的优势，他们的交易行为也是一个泊松过程，在每一天，都以到达率ε挂买单和卖单。 注意，这里所有的泊松过程都是互相独立的。我们可以把假设3用一个图表示出来，如下。

  

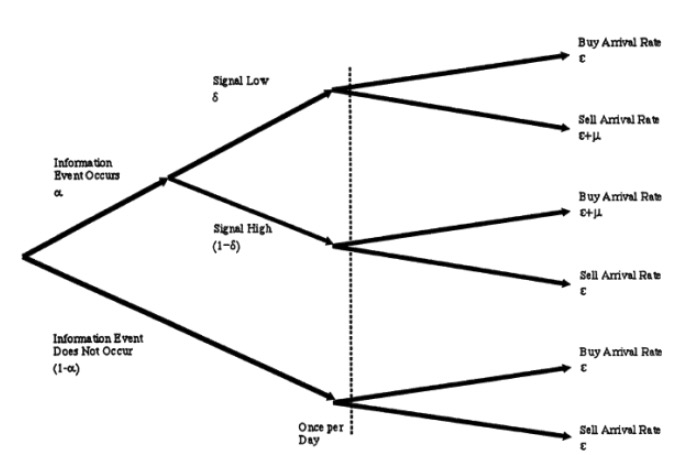
• 3 交易和价格的更新

  我们知道，做市商通常是牛逼闪闪的大公司来担任的。他们很聪明，在长期与IT和UT的斗争过程中，他们通过大量的历史数据分析，总结出了上面这个树状图中所有的模型参数。不过还好，他们没有知情交易者那么厉害，当某一个交易日即将开启的时候，他们不像知情交易者那样，对今天是否有大事发生了然于胸。他们所能做的，就是在这个交易日的交易进行的过程中，不断地通过其他交易者的报单行为，更新自己对于今天是否有事发生、是好事还是坏事的猜测（友情提醒：以上皆是假设）。这很容易理解。作为一个做市商，如果我在交易的过程中发现今天的买单特别多，那么我自然而然的会猜测，是不是有好事儿发生，于是我们就增加了自己对于“好事发生”这一事件的概率估计；相反的，如果我发现今天卖单特别多，那么我自然会增加自己对于“坏事发生”这一事件的概率估计。

  现在，让我们一起体验一把MM的角色，与IT和UT们斗争一番。在某个时间点t，我们把自己对于没有事、有好事，和有坏事发生的概率的猜测记为一个向量

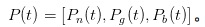  。很明显，在一天刚刚开始的时候，也就是 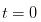的时候，我一个报单都没看到，所以我能做的就是认为，无事发生的概率为α,好事发生的概率为 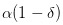，而坏事发生的概率为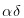

  应该如何更新这个概率呢？还好，我们做市商选的人都是懂贝叶斯公式的。在我们观察到一个卖单到来的情况下，我们利用贝叶斯法则，更新自己的概率估计。我们首先更新对于今天没有消息的概率估计，其表达式为

  

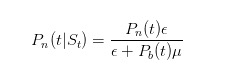
  这个式子的分子是说，当没有消息的时候，只有不知情交易者会以ε下卖单；而分母是说，不管什么时候，不知情交易者都会以ε下卖单，而知情交易者只会以在坏事发生时以μ下卖单。类似的，我们可以推得

  

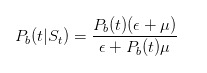
  以及

  

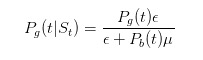
  在我们继续推导之前，让我们做一些简单的检验。刚刚我们说，如果我们看到一个卖单，那么我们对于“坏事发生”的概率估计就应该变大。是不是这样呢？我们可以做一个非常简单的推导

  

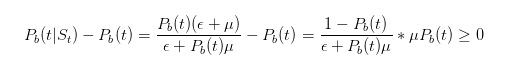
  由此可见，我们的推导印证了我们的直觉。

  有了更新后的概率之后，我们就可以计算出公允价格，以作为我们做市场报出的买价啦，其表达式为

  

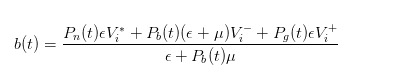
  通过类似的推导，我们可以发现，当一个买单发过来的时候，我们作为做市商报出的卖价应该为

  

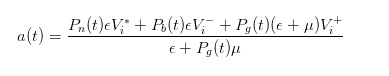
• 4 价格的变换后的价差表达式

  上面的买价和卖价的表达式还不够直观，我们可以引入在t时刻股票的期望价值来简化表达。我们有期望价值为

  

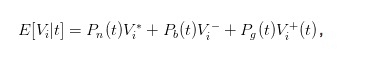
  这样，我们就可以将bid和ask的表达式变换为

  

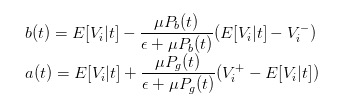
  于是，我们就可以把价差清晰的表达为

  

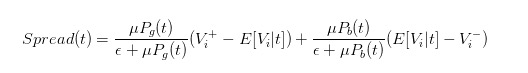
• 5 交易者行为对于价差的影响

  有了价差的表达式，我们就可以分析一下不同的交易者对于价差的影响啦！

  韭菜越多，价差越小。注意到，ε是不知情交易者（我们姑且称他们为“韭菜”吧）的到达率，如果有ε >> μ ，我们可以发现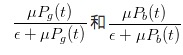， 这两项都将趋于0，这就意味着，spread也将趋于零。 没有韭菜，就没有交易。如果我们再走向另外一个极端，假设市场里面没有韭菜了，只有一群比猴还精的知情交易者，那么我们会悲惨的发现，我们挂出的价格将是 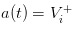和 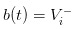，于是知情交易者发现自己无论如何买卖都将无利可图，市场必然死气沉沉（让我想到了国内的商品期权市场。。）。

  你看，我们基于一些假设，利用非常简单的数学推导，居然能够得到这样有趣而深刻的结论，这大概就是数学模型的巨大魅力吧。读完此文，我也希望大家能够善待韭菜，我们这些韭菜才是市场能够正常交易的保障！

[1] Easley, David, et al. “Liquidity, information, and infrequently traded stocks.” The Journal of Finance 51.4 (1996): 1405-1436.