Measuring Risk and Return - An Introduction to Markowitz Theory
 0
0
 1137
1137

Last week, when introducing How to Measure Position Risk - An Introduction to the VaR Method, it was mentioned that the risk of a portfolio is not equal to the risks of individual assets and is related to their price correlation. Taking two assets as an example, if their positive correlation is very strong, meaning they rise and fall together, then diversifying investments will not reduce risk. If there’s a strong negative correlation, diversified investments can reduce risk significantly. The natural question then arises: how do we maximize returns at a certain level of risk when investing in a portfolio? This leads us to Markowitz Theory, which we are going to introduce today.
The Modern Portfolio Theory (MPT), proposed by Harry Markowitz in 1952, is a mathematical framework for portfolio selection. It aims to maximize expected returns by choosing different combinations of risk assets while controlling risk. The core idea is that the prices of assets do not move completely in sync with each other (i.e., there is incomplete correlation between assets), and overall investment risk can be reduced through diversified asset allocation.
The Key Concept of Markowitz Theory
- Expected Return Rate: This is the return that investors expect to receive from holding assets or an investment portfolio, usually predicted based on historical return data.
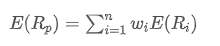
Where, 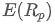 is the expected return of the portfolio,
is the expected return of the portfolio, 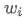 is the weight of the i-th asset in the portfolio,
is the weight of the i-th asset in the portfolio, 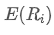 is the expected return of the i-th asset.
is the expected return of the i-th asset.
- Risk (Volatility or Standard Deviation): Used to measure the uncertainty of investment returns or the volatility of investments.
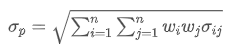
Where, 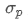 represents the total risk of the portfolio,
represents the total risk of the portfolio, 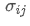 is the covariance of asset i and asset j, which measures the price change relationship between these two assets.
is the covariance of asset i and asset j, which measures the price change relationship between these two assets.
- Covariance: Measures the mutual relationship between price changes of two assets.
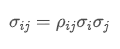
Where, 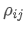 is the correlation coefficient of asset i and asset j,
is the correlation coefficient of asset i and asset j, 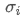 and
and 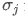 are respectively the standard deviations of asset i and asset j.
are respectively the standard deviations of asset i and asset j.
- Efficient Frontier: In the risk-return coordinate system, the efficient frontier is the set of investment portfolios that can provide the maximum expected return at a given level of risk.
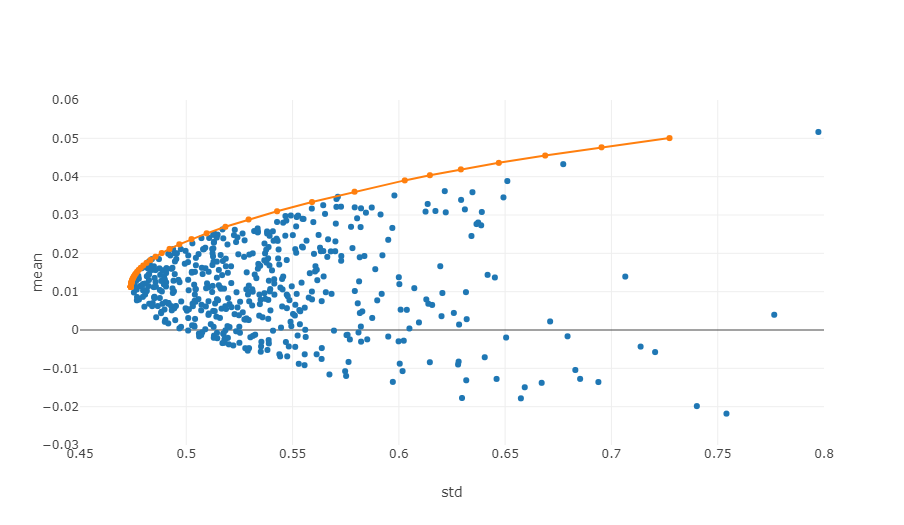
The diagram above is an illustration of an efficient frontier, where each point represents a different weighted investment portfolio. The x-axis denotes volatility, which equates to the level of risk, while the y-axis signifies return rate. Clearly, our focus lies on the upper edge of the graph as it achieves the highest returns at equivalent levels of risk.
In quantitative trading and portfolio management, applying these principles requires statistical analysis of historical data and using mathematical models to estimate expected returns, standard deviations and covariances for various assets. Then optimization techniques are used to find the best asset weight allocation. This process often involves complex mathematical operations and extensive computer processing - this is why quantitative analysis has become so important in modern finance. Next, we will illustrate how to optimize with specific Python examples.
Python Code Example for Finding the Optimal Combination Using Simulation Method
Calculating the Markowitz optimal portfolio is a multi-step process, involving several key steps, such as data preparation, portfolio simulation, and indicator calculation. Please refer to: https://plotly.com/python/v3/ipython-notebooks/markowitz-portfolio-optimization/
- Obtain market data:
Through the get_data function, obtain the historical price data of the selected digital currency. This is the necessary data for calculating returns and risks, which are used to build investment portfolios and calculate Sharpe ratios.
- Calculate Return Rate and Risk:
The calculate_returns_risk function was used to compute the annualized returns and annualized risk (standard deviation) for each digital currency. This is done to quantify the historical performance of each asset for use in an optimal portfolio.
- Calculate Markowitz Optimal Portfolio:
The calculate_optimal_portfolio function was used to simulate multiple investment portfolios. In each simulation, asset weights were randomly generated and then the expected return and risk of the portfolio were calculated based on these weights.
By randomly generating combinations with different weights, it is possible to explore multiple potential investment portfolios in order to find the optimal one. This is one of the core ideas of Markowitz’s portfolio theory.
The purpose of the entire process is to find the investment portfolio that yields the best expected returns at a given level of risk. By simulating multiple possible combinations, investors can better understand the performance of different configurations and choose the combination that best suits their investment goals and risk tolerance. This method helps optimize investment decisions, making investments more effective.
import numpy as np
import pandas as pd
import requests
import matplotlib.pyplot as plt
# Obtain market data
def get_data(symbols):
data = []
for symbol in symbols:
url = 'https://api.binance.com/api/v3/klines?symbol=%s&interval=%s&limit=1000'%(symbol,'1d')
res = requests.get(url)
data.append([float(line[4]) for line in res.json()])
return data
def calculate_returns_risk(data):
returns = []
risks = []
for d in data:
daily_returns = np.diff(d) / d[:-1]
annualized_return = np.mean(daily_returns) * 365
annualized_volatility = np.std(daily_returns) * np.sqrt(365)
returns.append(annualized_return)
risks.append(annualized_volatility)
return np.array(returns), np.array(risks)
# Calculate Markowitz Optimal Portfolio
def calculate_optimal_portfolio(returns, risks):
n_assets = len(returns)
num_portfolios = 3000
results = np.zeros((4, num_portfolios), dtype=object)
for i in range(num_portfolios):
weights = np.random.random(n_assets)
weights /= np.sum(weights)
portfolio_return = np.sum(returns * weights)
portfolio_risk = np.sqrt(np.dot(weights.T, np.dot(np.cov(returns, rowvar=False), weights)))
results[0, i] = portfolio_return
results[1, i] = portfolio_risk
results[2, i] = portfolio_return / portfolio_risk
results[3, i] = list(weights) # Convert weights to a list
return results
symbols = ['BTCUSDT','ETHUSDT', 'BNBUSDT','LINKUSDT','BCHUSDT','LTCUSDT']
data = get_data(symbols)
returns, risks = calculate_returns_risk(data)
optimal_portfolios = calculate_optimal_portfolio(returns, risks)
max_sharpe_idx = np.argmax(optimal_portfolios[2])
optimal_return = optimal_portfolios[0, max_sharpe_idx]
optimal_risk = optimal_portfolios[1, max_sharpe_idx]
optimal_weights = optimal_portfolios[3, max_sharpe_idx]
# Output results
print("Optimal combination:")
for i in range(len(symbols)):
print(f"{symbols[i]} Weight: {optimal_weights[i]:.4f}")
print(f"Expected return rate: {optimal_return:.4f}")
print(f"Expected risk (standard deviation): {optimal_risk:.4f}")
print(f"Sharpe ratio: {optimal_return / optimal_risk:.4f}")
# Visualized investment portfolio
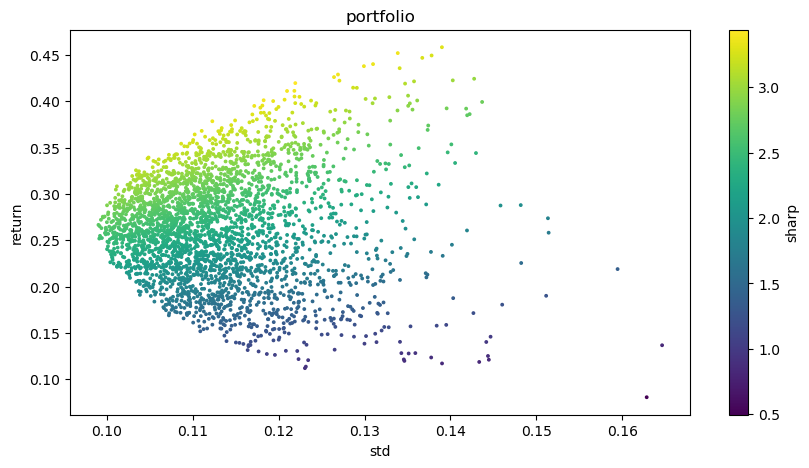
plt.figure(figsize=(10, 5))
plt.scatter(optimal_portfolios[1], optimal_portfolios[0], c=optimal_portfolios[2], marker='o', s=3)
plt.title('portfolio')
plt.xlabel('std')
plt.ylabel('return')
plt.colorbar(label='sharp')
plt.show()
Final output result: Optimal combination: Weight of BTCUSDT: 0.0721 Weight of ETHUSDT: 0.2704 Weight of BNBUSDT: 0.3646 Weight of LINKUSDT: 0.1892 Weight of BCHUSDT: 0.0829 Weight of LTCUSDT: 0.0209 Expected return rate: 0.4195 Expected risk (standard deviation): 0.1219 Sharpe ratio: 3.4403
- 低市值和低价,哪个更适合抄底?
- Bayes - Decoding the Mystery of Probability, Exploring the Mathematical Wisdom Behind Decision Making
- 贝叶斯--解码概率的奥秘,探寻决策背后的数学智慧
- The Advantages of Using FMZ's Extended API for Efficient Group Control Management in Quantitative Trading
- Price Performance After the Currency is Listed on Perpetual Contracts
- 使用FMZ的扩展API实现高效群控管理在量化交易中的优势
- 币种上线永续合约后的价格表现
- The Correlation Between the Rise and Fall of Currencies and Bitcoin
- 币种的涨跌与比特币的相关性关系
- A Brief Discussion on the Balance of Order Books in Centralized Exchanges
- 浅谈中心化交易所订单簿平衡
- 风险和回报的衡量——马科维茨理论介绍
- A Powerful Tool for Programmatic Traders: Incremental Update Algorithm for Calculating Mean and Variance
- 程序化交易者的利器:增量更新算法计算均值和方差
- Construction and Application of Market Noise
- PSY Factor Upgrade and Transformation
- High-Frequency Trading Strategy Analysis - Penny Jump
- Alternative Trading Ideas--K-line Area Trading Strategy
- 市场噪声的构建与应用
- PSY(心理线)因子升级与改造