FMEX排序解锁最优下单量优化
 0
0
 2258
2258

FMEX倒闭坑了不少人,但最近拿出了一个重启方案,并且制定了和原来挖矿类似的规则用于解锁债务。对交易挖矿,已经给出了一篇分析文章,https://www.fmz.com/bbs-topic/5834 。排序挖矿也有优化的空间。虽然人不应该两次踏入同一个坑,但在FMEX有债权的,不妨参考下,具体的能运行在FMZ量化平台的实盘策略可能也会放出。
FMEX排序解锁规则
定义每天中的每5分钟为一个排序解锁周期,每个周期分配交易对当日排序解锁额度的1/288。每个周期内,随机选取一个时间点,对该交易对买卖盘挂单情况做快照镜像,其中:
- 买1 按用户挂单金额占比 分配该排序解锁周期返还额度的1/4
- 卖1 按用户挂单金额占比 分配该排序解锁周期返还额度的1/4
- 买2到买5 这4档的挂单,按用户在每1档内的挂单金额占比 分别分配该排序解锁周期返还额度的1/40
- 卖2到卖5 这4档的挂单,按用户在每1档内的挂单金额占比 分别分配该排序解锁周期返还额度的1/40
- 买6到买10 这5档的挂单,按用户在每1档内的挂单金额占比 分别分配该排序解锁周期返还额度的1/50
- 卖6到卖10 这5档的挂单,按用户在每1档内的挂单金额占比 分别分配该排序解锁周期返还额度的1/50
- 买11到买15 这5档的挂单,按用户在每1档内的挂单金额占比 分别分配该排序解锁周期返还额度的1/100
- 卖11到卖15 这5档的挂单,按用户在每1档内的挂单金额占比 分别分配该排序解锁周期返还额度的1/100
当日某用户在某交易对的排序解锁的总返还,为用户在该交易对每个周期排序解锁所获额度返还的总和。
排序解锁收益
首先排序解锁的总收益为:
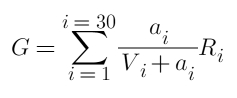
其中i表示其中一个位置,两方共30个位置,a为挂单量,R为解锁返还额度,V为已有订单总量。
与交易解锁不同,挂单并没有成本,这里的R只考虑相对大小就行,可以不用考虑USDT计价的绝对额度。如果我们决定了总挂单量,问题就变成了如何把订单分配到不同的位置上,达到收益G的最大化。简单的寻找最小挂单量的位置,全部挂上去,显然不是最优解。举一个例子,有三个位置的现有挂单量都是10,他们的R相同,我们设定的总挂单量为30,如果只选择一个位置挂单,最终总收益为0.75R,如果每个位置挂10,则最终收益为1.5R,可见有时分散挂单的收益更好。那么如何分配资金呢?
排序解锁的优化
最终我们的优化目标和约束条件为:
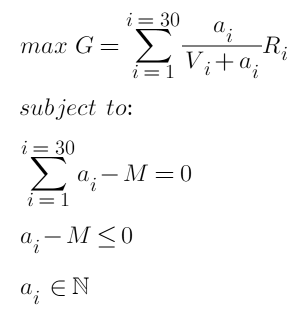
其中M为总挂单量。这是包含不等式的二次凸优化问题,满足KTT条件,并且解为整数。使用相应的包和凸优化求解器应该可以直接得出结果,返回每个位置最优的挂单量。但这显然不是我们要的答案,我们需要简化问题并且得到具体的求解步骤。
从一个简单的例子开始
只考虑两档的情况,目前的挂单量分别为10,20(分别称之为第一档,第二档),它们的解锁额度都为R,策略预备挂单总量为30,求该如何分配资金达到解锁额度最大化?这个问题看似简单,但不经过计算很难得出正确结论,读者不妨自己先想一下答案。
方案1:
寻找最小挂单位置,全部挂上去,总收益G=30/(30+10)=0.75R。这也是最容易想到的方案。
方案2:
每次分配1元,并且分配到能产生最大收益的地方,即挂单量最小的位置。则第1元会分配给第一档,第一档挂单量变为10+1,第2元也分给第一档…以此类推,直到累计分给第一档10元,此时可以随机选一个,当第一档总挂单超过20时,接下来分给第二档。最终结果为第一档分配20元,第二档分配10元,它们最终的挂单都为30。总收益G=20⁄30+10⁄30=R。这个方案比方案1好很多,并且也容易计算。
方案3:
可以设第一档分配a,第二档为30-a,则可以直接列出方程求导为0(过程不列了,和交易解锁的文章类似),算出最后的结果,公式为:
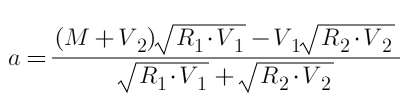
带入取整求得a=15。总收益G=15⁄25+15⁄35=1.0286R,比方案2要好,由于直接由公式得出,这是最优方案,读者可以验算一下。
结果可能和大家得预期不同,方案2明明每一元的分配都时当前情况下的最优解,怎么反而不是整体的最优解呢?这种情况很常见,局部的最优不一定是整体的最优,因为分配之前,里面的挂单量已经有投入的资金了,整体的效率需要考虑沉没成本。我们每步优化的目标是总体的效率最高而不是单次的收益最高。
### 具体的优化方案
终于开始实际的可行操作了,还是通过每次分配1元来简化问题。首先先衡量一下效率,用导数可以反映出每一份a对于G的贡献,这个贡献考虑到了累计的成本,而不是单次分配的收益,这个值越大说明总体对最终受益的贡献越大,显然,根据函数的图像,a=1,从有到无,效率最高,随后逐渐降低。
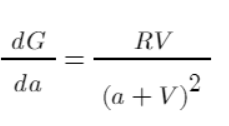
同样一上面那个简单的例子为例,分别算出他们分配资金后的效率,列出表格:
| 资金 | 1 | 2 |
|---|---|---|
| 1 | 0.0826 | 0.0454 |
| 2 | 0.069 | 0.0413 |
| 3 | 0.0592 | 0.0378 |
| 4 | 0.051 | 0.0347 |
| 5 | 0.0444 | 0.032 |
| … | … | … |
|12 | 0.0207 |0.0195| |13 | 0.0189 |0.0184| |14 | 0.0174 |0.0173| |15 | 0.016 |0.0163| |16 | 0.0148 |0.0154| |17 | 0.0137 |0.0146| |18 | 0.0128 |0.0139|
根据表格第1元分配给第一档,第2元分配给第一档…第5元分给第二档…以此类推,最后分配给第一档15元,第二档15元,恰好是我们根据方程计算的最优解。具体到30档的情况,算法一样,具体步骤为:
- 1.先检查所有挡位,如果V=0,则a=1,不再分配多余资金。
- 2.将总资金分配为N份,每次选择一个挡位分配。
- 3.计算每个挡位的效率=RV/pow(a+V,2),a代表该位置已累计分配的资金+本次分配资金。
- 4.将资金分配给效率最高的挡位,效率相同随机选一个。
- 5.循环3-4,直到资金分配完成
如果我们的总挂单量很大,每一元分配一次效率太低,可以把资金拆分为100份,每次分配一份,由于只是简单的运算排序,算法的效率很高。具体到执行层面,还有优化的空间,比如将我们的订单分为100个,这样每次调整时,只需要重新分配一下订单,不用全部撤除。也可以自行设定R值,给远离盘口以更多的权重,排序解锁和挂单解锁有重合部分,可以统一考虑,等等。
本文为FMZ量化平台原创文章,转账注明出处:https://www.fmz.com/bbs-topic-new/5843
- Python version iceberg commission strategy
- The Logic of Crypto Currency Futures Trading
- Bottom shape ZDZB strategy
- 多机器人行情共享解决方案
- 基于ARMA-EGARCH模型的比特币波动率建模和分析
- Solution of numerical calculation accuracy problem in JavaScript strategy design
- Teach you to encapsulate a Python strategy into a local file
- FMEX trading unlocks the optimal order volume optimization Part 2
- FMEX trading unlocks the optimal order volume optimization
- Analysis and Realization of Commodity Futures Volume Footprint Chart
- 调用钉钉接口实现机器人推送消息
- FMEX交易解锁最优下单量优化
- Simple Volatility EMV Strategy
- 手把手教你把一个Python策略封装成本地文件
- Deviation rate BIAS trading strategy
- Evaluation of backtest capital curve using "pyfolio" tool
- FMZ量化麦(My)语言--界面图表
- Python version of Commodity Futures Intertemporal Bollinger Hedge Strategy (Study purpose only)
- Interfacing with FMZ robot using "Tradingview" indicator
- FMZ量化麦语言(My)--麦语言交易类库参数