ChaoZhang
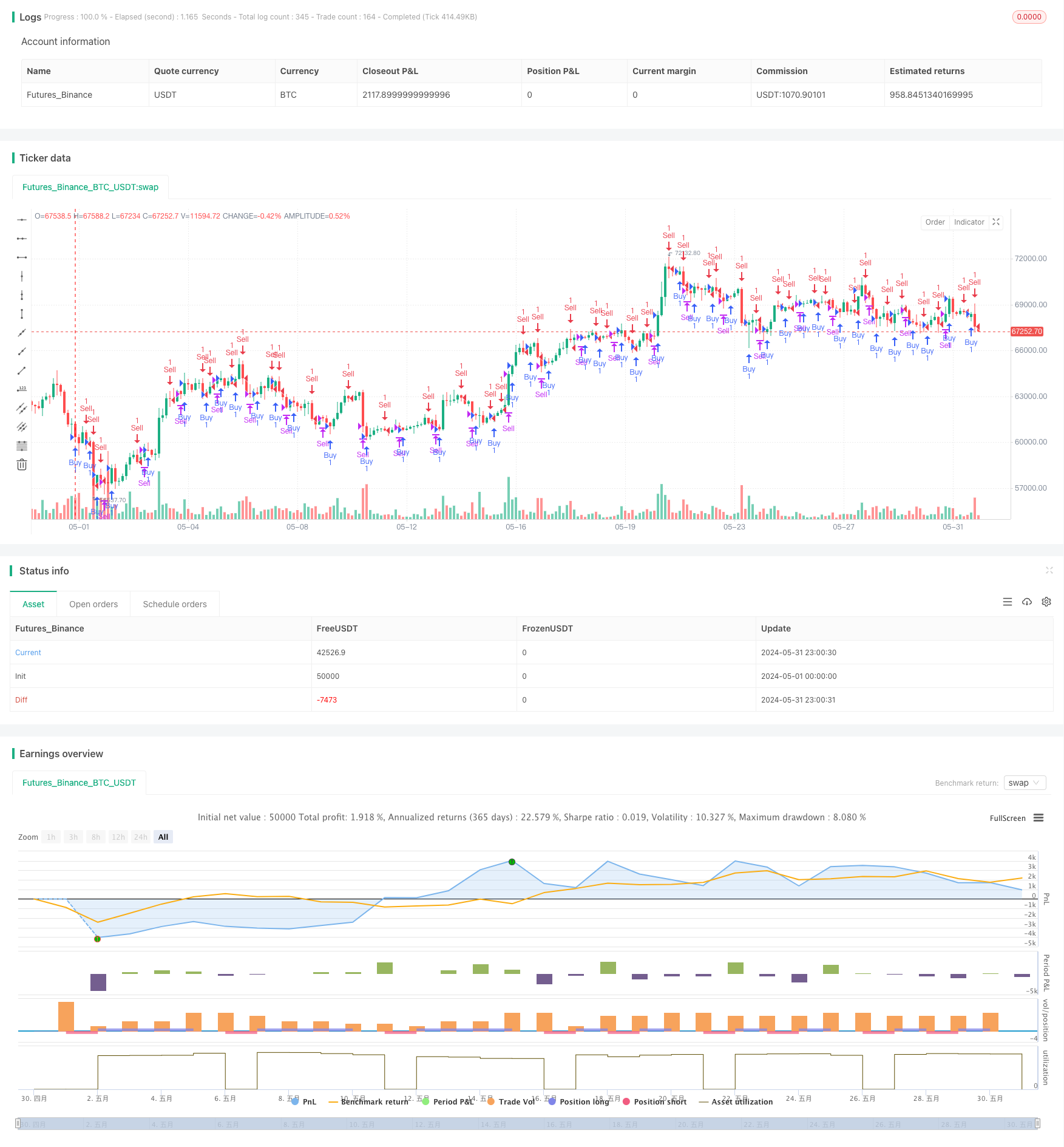
概述
马尔可夫链概率转换状态量化交易策略是一种基于马尔可夫链模型的创新型交易方法。该策略利用马尔可夫链的状态转换概率来预测市场走势,并据此做出交易决策。策略的核心思想是将市场状态分为多个离散的状态(如上涨、下跌和横盘),然后根据历史数据计算这些状态之间的转换概率,从而预测下一个可能的市场状态。
这种方法的独特之处在于它不仅考虑了当前的市场状态,还考虑了市场状态之间的转换动态。通过引入概率模型,该策略能够更好地捕捉市场的不确定性和波动性,从而在不同的市场环境中做出更加灵活和适应性强的交易决策。
策略原理
状态定义:策略将市场状态定义为三种 - 牛市(上涨)、熊市(下跌)和横盘(稳定)。这些状态通过比较当前收盘价与前一个收盘价来确定。
转换概率:策略使用9个输入参数来定义不同状态之间的转换概率。例如,
prob_bull_to_bull表示从牛市状态继续保持牛市状态的概率。状态转换逻辑:策略使用一个简化的转换逻辑来模拟马尔可夫链的状态转换过程。它使用一个计数器(
transition_counter)来模拟概率转换。交易信号生成:基于当前状态,策略生成买入、卖出或平仓信号。当状态为牛市时,策略开始做多;当状态为熊市时,策略开始做空;当状态为横盘时,策略平掉所有持仓。
策略优势
概率模型:通过引入马尔可夫链模型,该策略能够更好地捕捉市场的随机性和不确定性,这是传统技术分析方法难以实现的。
灵活性:策略可以通过调整转换概率参数来适应不同的市场环境,使其具有较强的适应性。
多状态考虑:与简单的趋势跟踪策略相比,该策略考虑了三种市场状态(上涨、下跌、横盘),能够更全面地把握市场动态。
风险管理:通过在横盘状态下平仓,策略内置了一定的风险管理机制,有助于控制潜在的损失。
可解释性:尽管使用了概率模型,但策略的逻辑相对简单明了,便于交易者理解和调整。
策略风险
参数敏感性:策略的表现高度依赖于设定的转换概率参数。不恰当的参数设置可能导致错误的交易信号。
滞后性:由于策略基于收盘价来判断状态,可能存在一定的滞后性,在快速变化的市场中可能错过重要的转折点。
过度简化:虽然马尔可夫链模型能捕捉一些市场动态,但仍然是对复杂金融市场的简化,可能忽略了一些重要的市场因素。
频繁交易:根据状态的频繁变化,策略可能生成过多的交易信号,增加交易成本。
市场适应性:在某些市场条件下(如长期趋势市场或高度波动的市场),策略可能表现不佳。
策略优化方向
引入更多状态:可以考虑引入更多的市场状态,如强势上涨、弱势上涨等,以更精细地刻画市场动态。
动态调整概率:可以开发一种机制,根据最近的市场表现动态调整转换概率,使策略更具适应性。
整合其他技术指标:可以将移动平均线、RSI等传统技术指标纳入状态判断逻辑,提高预测准确性。
优化状态判断逻辑:可以使用更复杂的逻辑来判断市场状态,如考虑多个时间周期的价格变动。
引入止损止盈:在策略中加入止损止盈机制,进一步控制风险和锁定利润。
回测和参数优化:对策略进行大规模的回测,使用遗传算法等方法来优化转换概率参数。
考虑交易成本:在策略逻辑中加入交易成本的考虑,避免过度频繁的交易。
总结
马尔可夫链概率转换状态量化交易策略是一种创新性的交易方法,它巧妙地将概率模型与传统的技术分析相结合。通过模拟市场状态的转换过程,该策略能够在捕捉市场趋势的同时,也考虑到了市场的随机性和不确定性。
虽然该策略存在参数敏感性和可能的过度简化等风险,但其灵活性和可解释性使其成为一个有潜力的交易工具。通过进一步的优化,如引入更多状态、动态调整概率、整合其他技术指标等,该策略有望在实际交易中取得更好的表现。
对于交易者来说,这种策略提供了一个新的思路,即如何利用概率模型来理解和预测市场行为。然而,在实际应用中,仍需要谨慎对待,进行充分的回测和风险评估,并根据具体的交易品种和市场环境进行适当的调整。
//@version=5
strategy("Markov Chain Strategy", overlay=true)
// Input parameters for transition probabilities
prob_bull_to_bull = input.float(0.7, title="Bull to Bull Transition Probability")
prob_bull_to_bear = input.float(0.2, title="Bull to Bear Transition Probability")
prob_bull_to_stagnant = input.float(0.1, title="Bull to Stagnant Transition Probability")
prob_bear_to_bull = input.float(0.3, title="Bear to Bull Transition Probability")
prob_bear_to_bear = input.float(0.5, title="Bear to Bear Transition Probability")
prob_bear_to_stagnant = input.float(0.2, title="Bear to Stagnant Transition Probability")
prob_stagnant_to_bull = input.float(0.4, title="Stagnant to Bull Transition Probability")
prob_stagnant_to_bear = input.float(0.3, title="Stagnant to Bear Transition Probability")
prob_stagnant_to_stagnant = input.float(0.3, title="Stagnant to Stagnant Transition Probability")
// Define price states
var float prev_close = na
var int state = na
// Calculate the current state
if (not na(prev_close))
if (close > prev_close)
state := 2 // Bull
else if (close < prev_close)
state := 1 // Bear
else
state := 3 // Stagnant
prev_close := close
// Transition logic (simplified)
var float transition_counter = 0
transition_counter := (transition_counter + 1) % 10
if (state == 2) // Bull
if (transition_counter < prob_bull_to_bull * 10)
state := 2
else if (transition_counter < (prob_bull_to_bull + prob_bull_to_bear) * 10)
state := 1
else
state := 3
else if (state == 1) // Bear
if (transition_counter < prob_bear_to_bull * 10)
state := 2
else if (transition_counter < (prob_bear_to_bull + prob_bear_to_bear) * 10)
state := 1
else
state := 3
else if (state == 3) // Stagnant
if (transition_counter < prob_stagnant_to_bull * 10)
state := 2
else if (transition_counter < (prob_stagnant_to_bull + prob_stagnant_to_bear) * 10)
state := 1
else
state := 3
// Strategy logic
if (state == 2)
strategy.entry("Buy", strategy.long)
else if (state == 1)
strategy.entry("Sell", strategy.short)
else
strategy.close("Buy")
strategy.close("Sell")
- 多周期指数移动平均交叉策略与期权交易建议系统
- Supertrend双重触发的多步移动止盈策略
- 自定义信号振荡器策略 (CSO)
- 多层级RSI回归交易策略与动态波动率调整
- 布林带动量交叉策略
- 超级三指标RSI-MACD-BB动量反转策略
- CCI动量背离趋势交易策略
- Hilo Activator MACD 动态止盈止损交易策略
- 动态止盈止损的双均线交叉交易策略
- RSI双周期均线反转策略与动态风险管理系统
- SMA 交叉策略结合 RSI 过滤和警报
- 动态唐奇安通道与简单移动平均线结合的量化策略
- 动态斐波那契回撤交易策略
- 布林带与指数移动平均结合交易策略
- EMA与超级趋势相结合的量化交易策略
- EMA、RSI、TA、多重指标交易策略
- SUPERTREND趋势追踪型多头止盈止损策略
- 基于交叉移动均线的趋势追踪自适应期望值评估策略
- EMA多头均线交叉策略
- EMA动态止损交易策略