সাতটি রিগ্রেশন কৌশল যা আপনার আয়ত্ত করা উচিত

**এই নিবন্ধটি রিগ্রেশন বিশ্লেষণ এবং এর সুবিধাগুলি ব্যাখ্যা করে, সাতটি সর্বাধিক ব্যবহৃত রিগ্রেশন কৌশল এবং এর মূল উপাদানগুলি যেমন লিনিয়ার রিগ্রেশন, লজিক্যাল রিগ্রেশন, মাল্টিপলারি রিগ্রেশন, ধাপে ধাপে রিগ্রেশন, স্ট্রিং রিগ্রেশন, হোল্ডিং রিগ্রেশন, ইলাস্টিক নেট রিগ্রেশন এবং এর মূল উপাদানগুলি যা আপনার আয়ত্ত করা উচিত। অবশেষে, সঠিক রিগ্রেশন মডেল চয়ন করার মূল কারণগুলি সম্পর্কে জানুন। ** ** এই নিবন্ধটি রিগ্রেশন বিশ্লেষণ এবং এর উপকারিতা ব্যাখ্যা করে, এবং সবচেয়ে বেশি ব্যবহৃত সাতটি রিগ্রেশন কৌশল এবং এর মূল উপাদানগুলি যেমন লিনিয়ার রিগ্রেশন, লজিক্যাল রিগ্রেশন, মাল্টিপোলার রিগ্রেশন, ধাপে ধাপে রিগ্রেশন, স্ট্রিং রিগ্রেশন, সুইচ রিগ্রেশন, ইলাস্টিক নেট রিগ্রেশন ইত্যাদির উপর আলোকপাত করে এবং অবশেষে সঠিক রিগ্রেশন মডেলটি বেছে নেওয়ার মূল উপাদানগুলি উপস্থাপন করে।**

• ### রিগ্রেশনাল বিশ্লেষণ কি?

রিগ্রেশনাল বিশ্লেষণ একটি ভবিষ্যদ্বাণীমূলক মডেলিং কৌশল যা কারণ পরিবর্তনশীল (লক্ষ্য) এবং স্ব-পরিবর্তক (প্রদর্শক) এর মধ্যে সম্পর্ক নিয়ে গবেষণা করে। এই কৌশলটি সাধারণত ভবিষ্যদ্বাণী বিশ্লেষণ, টাইম সিকোয়েন্স মডেলিং এবং আবিষ্কৃত পরিবর্তনশীলগুলির মধ্যে কার্যকারিতা সম্পর্ক নিয়ে গবেষণা করা হয়। উদাহরণস্বরূপ, ড্রাইভারের অনিয়ন্ত্রিত ড্রাইভিং এবং সড়ক ট্র্যাফিক দুর্ঘটনার সংখ্যার মধ্যে সম্পর্ক, সবচেয়ে ভাল গবেষণা পদ্ধতি হল রিগ্রেশন।

রিগ্রেশন অ্যানালিসিস একটি গুরুত্বপূর্ণ সরঞ্জাম যা আমরা ডেটা মডেলিং এবং বিশ্লেষণের জন্য ব্যবহার করি। এখানে, আমরা কার্ভ/লাইন ব্যবহার করি এই ডেটা পয়েন্টগুলিকে একত্রিত করার জন্য, এইভাবে, কার্ভ বা লাইন থেকে ডেটা পয়েন্টের দূরত্বের পার্থক্য ন্যূনতম। আমি পরবর্তী অংশে এটি বিস্তারিতভাবে ব্যাখ্যা করব।

• ### কেন আমরা রিগ্রেশন অ্যানালিসিস ব্যবহার করি?

যেমন উপরে উল্লেখ করা হয়েছে, রিগ্রেশন বিশ্লেষণ দুই বা ততোধিক ভেরিয়েবলের মধ্যে সম্পর্ককে অনুমান করে। নীচে, আসুন এটি বোঝার জন্য একটি সহজ উদাহরণ দেইঃ

উদাহরণস্বরূপ, বর্তমান অর্থনৈতিক অবস্থার মধ্যে, আপনি যদি একটি কোম্পানির বিক্রয় বৃদ্ধির অনুমান করতে চান। এখন, আপনার কাছে কোম্পানির সর্বশেষ তথ্য রয়েছে, যা দেখায় যে বিক্রয় বৃদ্ধির পরিমাণ অর্থনৈতিক বৃদ্ধির প্রায় ২.৫ গুণ। তাহলে রিগ্রেশন অ্যানালিসিস ব্যবহার করে, আমরা বর্তমান এবং অতীতের তথ্যের উপর ভিত্তি করে ভবিষ্যতে কোম্পানির বিক্রয় সম্পর্কে ভবিষ্যদ্বাণী করতে পারি।

রিগ্রেশন বিশ্লেষণ ব্যবহারের অনেক সুবিধা রয়েছে। বিশেষত নিম্নলিখিতগুলিঃ

এটি স্ব-পরিবর্তক এবং কারণ-পরিবর্তকের মধ্যে উল্লেখযোগ্য সম্পর্ক প্রদর্শন করে;

এটি একাধিক স্ব-পরিবর্তক দ্বারা একটি কারণ-পরিবর্তকের উপর প্রভাবের তীব্রতা নির্দেশ করে।

রিগ্রেশন বিশ্লেষণ আমাদেরকে বিভিন্ন স্কেলে পরিমাপ করা ভেরিয়েবলের মধ্যে পারস্পরিক প্রভাবের তুলনা করার অনুমতি দেয়, যেমন দামের পরিবর্তনের সাথে প্রচারমূলক ক্রিয়াকলাপের সংখ্যার মধ্যে সম্পর্ক। এটি বাজার গবেষক, ডেটা বিশ্লেষক এবং ডেটা বিজ্ঞানীদের ভবিষ্যদ্বাণীমূলক মডেল তৈরির জন্য সর্বোত্তম ভেরিয়েবলের একটি সেট বাদ দিতে এবং অনুমান করতে সহায়তা করে।

• ### আমাদের কাছে কতগুলো রিগ্রেশন প্রযুক্তি আছে?

বিভিন্ন ধরণের রিগ্রেশন টেকনিক রয়েছে যা ভবিষ্যদ্বাণী করার জন্য ব্যবহৃত হয়। এই টেকনিকগুলির প্রধানত তিনটি পরিমাপ রয়েছেঃ স্ব-পরিবর্তনের সংখ্যা, স্ব-পরিবর্তনের ধরণ এবং রিগ্রেশন লাইনের আকৃতি। আমরা নীচের অংশে তাদের বিস্তারিতভাবে আলোচনা করব।

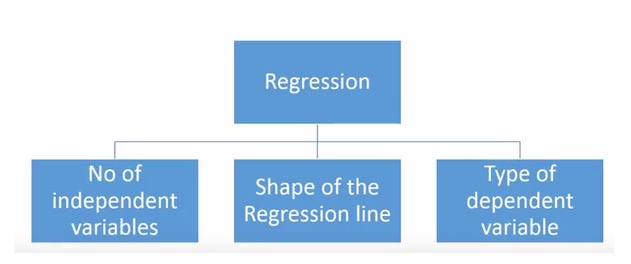
সৃজনশীল ব্যক্তিদের জন্য, আপনি যদি উপরের প্যারামিটারগুলির একটি সমন্বয় ব্যবহার করতে প্রয়োজন বোধ করেন তবে আপনি এমন একটি রিগ্রেশন মডেলও তৈরি করতে পারেন যা ব্যবহার করা হয়নি। তবে আপনি শুরু করার আগে, নীচের সর্বাধিক ব্যবহৃত রিগ্রেশন পদ্ধতিগুলি সম্পর্কে জানুনঃ

• ১. লিনিয়ার রিগ্রেশন

  এটি সবচেয়ে পরিচিত মডেলিং কৌশলগুলির মধ্যে একটি। লিনিয়ার রিগ্রেশন সাধারণত ভবিষ্যদ্বাণীমূলক মডেল শেখার জন্য একটি পছন্দের কৌশল। এই প্রযুক্তিতে, কারণ পরিবর্তনশীল ধারাবাহিক, স্ব-পরিবর্তক ধারাবাহিক বা বিচ্ছিন্ন হতে পারে, রিগ্রেশন লাইনগুলির বৈশিষ্ট্যটি লিনিয়ার।

  লিনিয়ার রিগ্রেশন সর্বোত্তম সামঞ্জস্যপূর্ণ রেখার ব্যবহার করে (অর্থাৎ রিগ্রেশন লাইন) কারণ পরিবর্তনশীল (Y) এবং এক বা একাধিক স্বতন্ত্র পরিবর্তনশীল (X) এর মধ্যে একটি সম্পর্ক স্থাপন করে।

  এবং আমি এটাকে একটা সমীকরণ দিয়ে দেখাবো, যেটা হল Y=a+b*X + e, যেখানে a হল বিভাজক, b হল সরলরেখার তির্যকতা, এবং e হল ত্রুটি। এই সমীকরণটি একটি প্রদত্ত পূর্বাভাস ভেরিয়েবলের উপর ভিত্তি করে লক্ষ্য ভেরিয়েবলের মান পূর্বাভাস দিতে পারে।

  

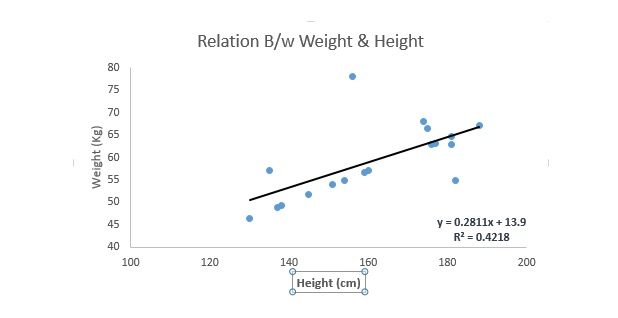
  এক-পরিসীমীয় রিগ্রেশন এবং বহু-পরিসীমীয় রিগ্রেশনের মধ্যে পার্থক্য হল যে, বহু-পরিসীমীয় রিগ্রেশনের ([[:en:Multiple linear regression]]) একটি স্বতন্ত্র পরিবর্তনশীল থাকে, যখন এক-পরিসীমীয় রিগ্রেশনের ([[:en:Multiple linear regression]]) সাধারণত একটি স্বতন্ত্র পরিবর্তনশীল থাকে। এখন প্রশ্ন হল, আমরা কিভাবে একটি সর্বোত্তম মিলিত লাইন পেতে পারি?

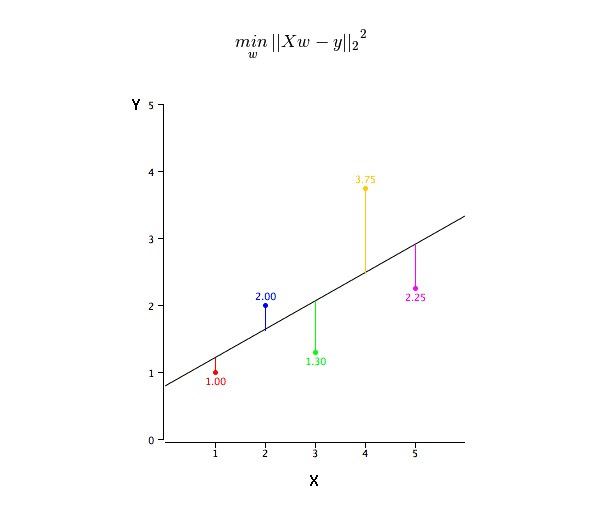
  কিভাবে সেরা ফিট লাইন (a এবং b) এর মান পাওয়া যায়?

  এই সমস্যাটি সহজেই সর্বনিম্ন দ্বিগুণের সাথে সম্পন্ন করা যায়। সর্বনিম্ন দ্বিগুণটিও রিগ্রেশন লাইনকে সামঞ্জস্য করার জন্য সর্বাধিক ব্যবহৃত পদ্ধতি। পর্যবেক্ষণের তথ্যের জন্য, এটি প্রতিটি ডেটা পয়েন্টকে লাইনের সাথে সংযুক্ত করে উল্লম্ব বিচ্যুতির বর্গক্ষেত্রকে সর্বনিম্ন করে সর্বোত্তম সামঞ্জস্যের লাইনটি গণনা করে। কারণ যোগ করার সময়, বিচ্যুতিটি প্রথম বর্গক্ষেত্র হয়, তাই ইতিবাচক এবং নেতিবাচক মানগুলি অফসেট হয় না।

  

  আমরা R-square সূচক ব্যবহার করে মডেলের পারফরম্যান্সের মূল্যায়ন করতে পারি। এই সূচকগুলির বিস্তারিত তথ্যের জন্য, পড়ুনঃ মডেল পারফরম্যান্স সূচক পার্ট 1, পার্ট 2 ।

  মূল কথাঃ

  • স্ব-পরিবর্তক এবং কারণ-পরিবর্তকের মধ্যে অবশ্যই একটি রৈখিক সম্পর্ক থাকতে হবে
  • মাল্টিপল রিটার্নের মধ্যে একাধিক সহ-রৈখিকতা, স্ব-সম্পর্কিততা এবং বৈষম্য রয়েছে।
  • লিনিয়ার রিগ্রেশন অস্বাভাবিকতার প্রতি অত্যন্ত সংবেদনশীল। এটি রিগ্রেশন লাইনকে প্রভাবিত করে এবং শেষ পর্যন্ত পূর্বাভাসকে প্রভাবিত করে।
  • মাল্টিপল কোমোলিনিয়ারিটি ফ্যাক্টর অনুমান মানের পার্থক্য বাড়ায়, যা মডেলের সামান্য পরিবর্তনগুলির সাথে অনুমানকে অত্যন্ত সংবেদনশীল করে তোলে। ফলস্বরূপ ফ্যাক্টর অনুমান মান অস্থির হয়
  • একাধিক স্বতন্ত্রের ক্ষেত্রে, আমরা অগ্রসর নির্বাচন পদ্ধতি, পশ্চাদপসরণ অপসারণ পদ্ধতি এবং ধাপে ধাপে বাছাই পদ্ধতি ব্যবহার করে সর্বাধিক গুরুত্বপূর্ণ স্বতন্ত্র নির্বাচন করতে পারি।

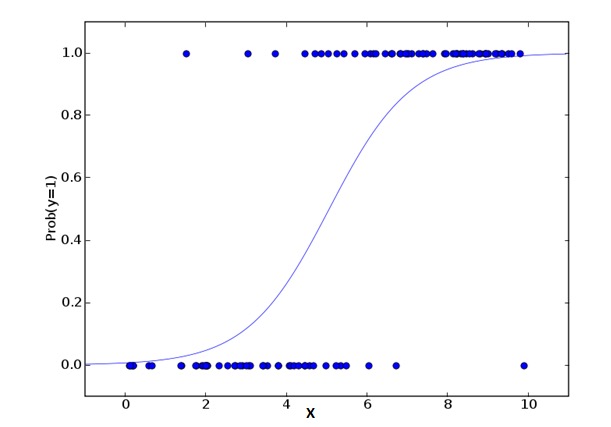
• 2. Logistic Regression লজিক্যাল রিগ্রেশন

  লজিক্যাল রিগ্রেশন হলো এমন একটি সম্ভাব্যতা যা হিসাব করা যায় যে, কোন ঘটনা হল Success=Success এবং কোন ঘটনা হল Failure=Failure। আমরা যখন লজিক্যাল রিগ্রেশন ব্যবহার করি, তখন আমরা বুঝতে পারি যে, ভেরিয়েবলের ধরন হচ্ছে Binary ((¹⁄₀, true/false, yes/no) ভেরিয়েবল। এখানে, Y এর মান 0 থেকে 1 পর্যন্ত, যা নিম্নলিখিত সমীকরণ দ্বারা প্রকাশ করা যায়।

  odds= p/ (1-p) = probability of event occurrence / probability of not event occurrence
  ln(odds) = ln(p/(1-p))
  logit(p) = ln(p/(1-p)) = b0+b1X1+b2X2+b3X3....+bkXk
  

  উপরের সূত্রের মধ্যে, p এর একটি নির্দিষ্ট বৈশিষ্ট্যের সম্ভাবনা রয়েছে। আপনি এই প্রশ্নটি জিজ্ঞাসা করতে পারেনঃ আমরা কেন সূত্রটিতে লগ ব্যবহার করব?

  যেহেতু এখানে আমরা ব্যবহার করছি দ্বিপদী বন্টন ((কারণ ভেরিয়েবল), তাই আমাদের এই বন্টনটির জন্য একটি সর্বোত্তম সংযোগ ফাংশন বেছে নিতে হবে। এটি হল Logit ফাংশন। উপরের সমীকরণে, নমুনার সর্বাধিক সম্ভাব্য অনুমান মানগুলি পর্যবেক্ষণ করে প্যারামিটারগুলি বেছে নেওয়া হয়েছে, বরং স্কোয়ার এবং ত্রুটিগুলিকে ক্ষুদ্রতর করার পরিবর্তে (যেমন সাধারণ প্রত্যাবর্তনে ব্যবহৃত হয়) ।

  

  মূল কথাঃ

  • এটি ব্যাপকভাবে ব্যবহৃত হয় শ্রেণীবিভাগের প্রশ্নের জন্য।
  • লজিক্যাল রিগ্রেশন বলে যে স্ব-পরিবর্তক এবং ক্রম-পরিবর্তক সম্পর্কটি লিনিয়ার নয়। এটি বিভিন্ন ধরণের সম্পর্ককে মোকাবেলা করতে পারে, কারণ এটি প্রাক্কলিত আপেক্ষিক ঝুঁকি সূচক OR এর জন্য একটি অ-লিনিয়ার লগ রূপান্তর ব্যবহার করে।
  • ওভারফিট এবং অ-ফিট এড়াতে, আমাদের সকল গুরুত্বপূর্ণ ভেরিয়েবল অন্তর্ভুক্ত করা উচিত। এটি নিশ্চিত করার একটি ভাল উপায় হল ধাপে ধাপে বাছাই পদ্ধতি ব্যবহার করে লজিক্যাল রিটার্নের অনুমান করা।
  • এটির জন্য বড় পরিমাণে নমুনা প্রয়োজন, কারণ নমুনার সংখ্যার সাথে, খুব সম্ভবত অনুমান করা প্রভাবটি সাধারণ ন্যূনতম দ্বিগুণের চেয়ে খারাপ।
  • স্ব-পরিবর্তকগুলিকে একে অপরের সাথে সম্পর্কিত করা উচিত নয়, অর্থাৎ একাধিক সহ-লাইনযুক্ত নয়। যাইহোক, বিশ্লেষণ এবং মডেলিংয়ের ক্ষেত্রে, আমরা শ্রেণিবদ্ধকরণ পরিবর্তনশীলগুলির মধ্যে পারস্পরিক প্রভাব অন্তর্ভুক্ত করার জন্য নির্বাচন করতে পারি।
  • যদি একটি ভেরিয়েবলের মান একটি ক্রমিক ভেরিয়েবল হয়, তবে এটিকে ক্রমিক লজিক রিগ্রেশন বলা হয়।
  • যদি ভেরিয়েবলটি একাধিক শ্রেণীর হয়, তবে এটিকে মাল্টিপল লজিকাল রিগ্রেশন বলা হয়।

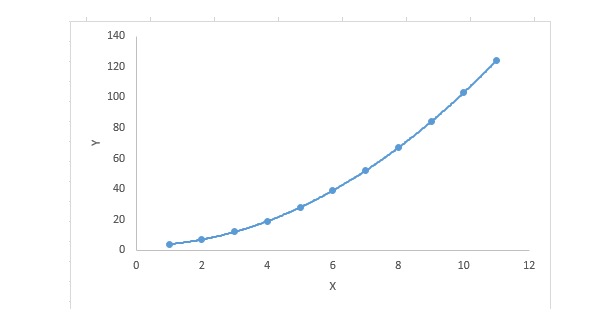
• ৩. পলিনোমিয়াল রিগ্রেশন

  একটি রিগ্রেশন সমীকরণের জন্য, যদি স্ব-পরিবর্তকের সূচকটি 1 এর চেয়ে বড় হয়, তবে এটি একটি বহুপদী রিগ্রেশন সমীকরণ। নিম্নলিখিত সমীকরণটি দেখায়ঃ

  y=a+b*x^2
  

  এই রিগ্রেশন টেকনোলজিতে, সর্বোত্তম মিলিত লাইনটি একটি সরল লাইন নয়। এটি একটি বক্ররেখা যা ডেটা পয়েন্টগুলিকে মিলিত করতে ব্যবহৃত হয়।

  

  বিষয়ঃ

  • যদিও একটি প্ররোচনা একটি উচ্চতর বহুপদীকে সামঞ্জস্য করতে পারে এবং কম ত্রুটি পেতে পারে, তবে এটি ওভারফিট হতে পারে। আপনাকে নিয়মিতভাবে সম্পর্কযুক্ত চিত্র আঁকতে হবে যাতে আপনি দেখতে পারেন যে ফিটটি কী এবং যুক্তিসঙ্গত ফিটটি নিশ্চিত করার জন্য নিবদ্ধ থাকুন যাতে কোনও ওভারফিট বা ডেবিট ফিট না থাকে। নীচে একটি চিত্র রয়েছে যা বুঝতে সহায়তা করেঃ

  

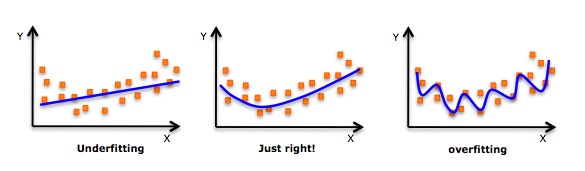
  • স্পষ্টতই উভয় প্রান্তে বক্ররেখার পয়েন্টগুলি সন্ধান করুন এবং দেখুন যে এই আকার এবং প্রবণতাগুলি অর্থবহ কিনা। উচ্চতর স্তরের বহুপদীগুলি শেষ পর্যন্ত অদ্ভুত সিদ্ধান্তের ফলাফল তৈরি করতে পারে।

• ৪. ধাপে ধাপে রিগ্রেশন

  একাধিক স্বতন্ত্র ভেরিয়েবলের সাথে কাজ করার সময় আমরা এই ফর্মটি ব্যবহার করতে পারি। এই প্রযুক্তিতে, স্বতন্ত্র ভেরিয়েবলের নির্বাচন একটি স্বয়ংক্রিয় প্রক্রিয়াতে সম্পন্ন হয়, যার মধ্যে অ-মানবিক অপারেশন অন্তর্ভুক্ত রয়েছে।

  এই কৃতিত্বটি গুরুত্বপূর্ণ ভেরিয়েবলগুলি সনাক্ত করার জন্য পরিসংখ্যানগত মানগুলি যেমন R-square, t-stats এবং AIC সূচকগুলি পর্যবেক্ষণ করে। ধাপে ধাপে রিগ্রেশন নির্দিষ্ট মানদণ্ডের উপর ভিত্তি করে সমান্তরাল ভেরিয়েবলগুলি যোগ / মুছে ফেলার মাধ্যমে মডেলটি ফিট করে। নীচে কয়েকটি সর্বাধিক ব্যবহৃত ধাপে ধাপে রিগ্রেশন পদ্ধতি রয়েছেঃ

  • স্ট্যান্ডার্ড ধাপে ধাপে রিগ্রেশন পদ্ধতি দুটি কাজ করে: প্রতিটি ধাপে প্রয়োজনীয় পূর্বাভাস যোগ করা এবং বাদ দেওয়া।
  • ফরোয়ার্ড সিলেকশন পদ্ধতিটি মডেলের সবচেয়ে উল্লেখযোগ্য ভবিষ্যদ্বাণী দিয়ে শুরু করে এবং তারপরে প্রতিটি ধাপে একটি পরিবর্তনশীল যোগ করে।
  • পশ্চাৎপদ অপসারণ পদ্ধতিটি মডেলের সমস্ত পূর্বাভাসের সাথে একই সময়ে শুরু হয় এবং তারপরে প্রতিটি ধাপে ন্যূনতম উল্লেখযোগ্য পরিবর্তনশীলকে সরিয়ে দেয়।
  • এই মডেলিং প্রযুক্তির উদ্দেশ্য হল সর্বনিম্ন সংখ্যক পূর্বাভাস ভেরিয়েবল ব্যবহার করে পূর্বাভাস ক্ষমতা সর্বাধিক করা। এটি উচ্চ মাত্রিক ডেটাসেটগুলির সাথে কাজ করার একটি উপায়।

• ৫. রিজ রিগ্রেশন

  রিগ্রেশন বিশ্লেষণ এমন একটি কৌশল যা বহু-কোমোনিয়ালিটি (অনুসরণীয়ভাবে সংশ্লিষ্ট) ডেটা ব্যবহার করে। বহু-কোমোনিয়ালিটির ক্ষেত্রে, যদিও সর্বনিম্ন দ্বিগুণকরণ (অনুসরণীয়ভাবে OLS) প্রতিটি ভেরিয়েবলের জন্য ন্যায্য, তবে তাদের পার্থক্য এত বড় যে পর্যবেক্ষণের মানটি বিচ্যুত হয় এবং সত্যিকারের মান থেকে দূরে চলে যায়। রিগ্রেশনকে একটি স্ট্যান্ডার্ড ত্রুটি হ্রাস করার জন্য রিগ্রেশন অনুমানের উপর একটি বিচ্যুতি যোগ করা হয়।

  উপরের লাইন রিগ্রেশন সমীকরণটি মনে আছে? এটাকে এভাবে প্রকাশ করা যায়ঃ

  y=a+ b*x
  

  এই সমীকরণে একটি ত্রুটি আছে। সম্পূর্ণ সমীকরণ হল:

  y=a+b*x+e (error term),  [error term is the value needed to correct for a prediction error between the observed and predicted value]
  => y=a+y= a+ b1x1+ b2x2+....+e, for multiple independent variables.
  

  একটি রৈখিক সমীকরণে, ভবিষ্যদ্বাণী ত্রুটি দুটি উপ-পরিমাণে বিভক্ত হতে পারে। একটি হল বিচ্যুতি এবং অন্যটি হ’ল বিভাজন। ভবিষ্যদ্বাণী ত্রুটিগুলি এই দুটি অনুপাত বা উভয়ই দ্বারা সৃষ্ট হতে পারে। এখানে আমরা বিভাজন দ্বারা সৃষ্ট সংশ্লিষ্ট ত্রুটিগুলি নিয়ে আলোচনা করব।

  ক্যালকুলেটর রিগ্রেশন সংক্ষেপণ প্যারামিটার λ ((lambda) ব্যবহার করে মাল্টিপল কোমোলিউনিটি সমস্যা সমাধান করে। নিচের সূত্রটি দেখুন

  

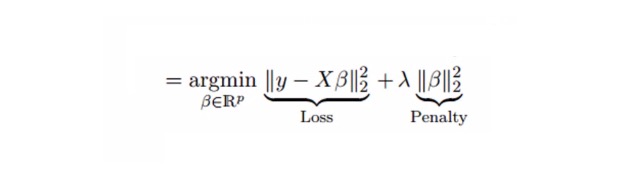
  এই সূত্রের দুটি উপাদান রয়েছে। প্রথমটি হল সর্বনিম্ন দ্বিগুণ এবং অন্যটি হল β2 ((β- বর্গক্ষেত্র) এর λ গুণ, যেখানে β সংশ্লিষ্ট সহগ। সংক্ষিপ্তকরণের জন্য এটিকে সর্বনিম্ন দ্বিগুণের সাথে যুক্ত করুন যাতে একটি খুব কম পার্থক্য পাওয়া যায়।

  মূল কথাঃ

  • ধ্রুবসংখ্যা ব্যতীত, এই রিগ্রেশনটি সর্বনিম্ন দ্বিগুণ রিগ্রেশনের মতই অনুমান করা হয়।
  • এটি সংশ্লিষ্ট কোয়ালিটির মানকে সঙ্কুচিত করে, কিন্তু শূন্যে পৌঁছায় না, যা দেখায় যে এটির কোনও বৈশিষ্ট্য নির্বাচন বৈশিষ্ট্য নেই
  • এটি একটি নিয়মাবলী পদ্ধতি এবং L2 নিয়মাবলী ব্যবহার করা হয়।

• ৬. লাসো রিগ্রেশন

  লাসো (Least Absolute Shrinkage and Selection Operator) -এর মতই এটি রিগ্রেশন ফ্যাক্টরটির পরম মানের আকারকে শাস্তি দেয়। উপরন্তু, এটি পরিবর্তনশীলতা হ্রাস করতে এবং লিনিয়ার রিগ্রেশন মডেলের নির্ভুলতা বাড়াতে সক্ষম। নিচের সূত্রটি দেখুনঃ

  

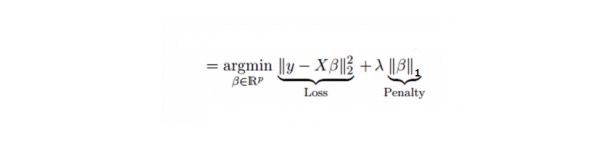
  লাসো রিগ্রেশনটি রিজ রিগ্রেশন থেকে কিছুটা আলাদা, এটি একটি শাস্তি ফাংশন ব্যবহার করে যা একটি পরম মান, একটি বর্গক্ষেত্রের পরিবর্তে। এর ফলে শাস্তি ((বা সীমাবদ্ধ অনুমানের পরম মানের সমষ্টি) মানটি কিছু প্যারামিটার অনুমানের ফলাফলকে শূন্য করে দেয়। শাস্তি মানটি যত বেশি ব্যবহার করা হয়, ততই আরও অনুমান করা হয় যাতে ক্ষুদ্রতর মানটি শূন্যের কাছাকাছি চলে যায়। এর ফলে আমরা প্রদত্ত n টি ভেরিয়েবলের মধ্যে থেকে একটি ভেরিয়েবল নির্বাচন করব।

  মূল কথাঃ

  • ধ্রুবসংখ্যা ব্যতীত, এই রিগ্রেশনটি সর্বনিম্ন দ্বিগুণ রিগ্রেশনের মতই অনুমান করা হয়।
  • এটির সংকোচনের কোয়ার্টার প্রায় শূন্য ((শূন্যের সমান), যা প্রকৃতপক্ষে বৈশিষ্ট্য নির্বাচনে সহায়তা করে;
  • এটি একটি নিয়মাবলী পদ্ধতি, L1 নিয়মাবলী ব্যবহার করে;
  • যদি একটি পূর্বাভাস ভেরিয়েবলের একটি সেট অত্যন্ত সংশ্লিষ্ট হয়, লাসো তার মধ্যে একটি ভেরিয়েবল নির্বাচন করে এবং অন্যটিকে শূন্যে সঙ্কুচিত করে।

• ৭. ইলাস্টিক নেট-এ ফিরে আসা

  ElasticNet হল Lasso এবং Ridge regression প্রযুক্তির মিশ্রণ। এটি L1 ব্যবহার করে প্রশিক্ষণ দেয় এবং L2 কে নিয়মীয়াকরণ ম্যাট্রিক্স হিসাবে অগ্রাধিকার দেয়। যখন একাধিক সম্পর্কিত বৈশিষ্ট্য থাকে, তখন ElasticNet দরকারী। Lasso এলোমেলোভাবে তাদের মধ্যে একটি বেছে নেবে, এবং ElasticNet দুটি বেছে নেবে।

  

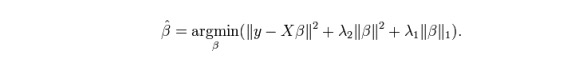
  Lasso এবং Ridge এর মধ্যে প্রকৃত সুবিধা হল যে এটি ElasticNet কে Ridge এর কিছু স্থায়িত্বকে পুনরাবৃত্ত অবস্থায় উত্তরাধিকার করার অনুমতি দেয়।

  মূল কথাঃ

  • এটি একটি গোষ্ঠীগত প্রভাব সৃষ্টি করে যেখানে অনেকগুলি সংশ্লিষ্ট পরিবর্তনশীল রয়েছে।
  • কোন সীমাবদ্ধতা নেই যে কোন ভেরিয়েবল নির্বাচন করতে;
  • এটি ডাবল কম্প্রেশন সহ্য করতে পারে।
  • এই সাতটি সবচেয়ে বেশি ব্যবহৃত রিগ্রেশন কৌশল ছাড়াও, আপনি অন্যান্য মডেল যেমন Bayesian, Ecological এবং Robust regression দেখতে পারেন।

• কিভাবে সঠিক রিগ্রেশন মডেল বেছে নেবেন?

  যখন আপনি কেবল একটি বা দুটি কৌশল জানেন তখন জীবন অনেক সহজ হয়ে যায়। আমি জানি একটি প্রশিক্ষণ প্রতিষ্ঠান তাদের শিক্ষার্থীদের বলেছে যে যদি ফলাফল ধারাবাহিক হয় তবে লিনিয়ার রিগ্রেশন ব্যবহার করুন। যদি এটি দ্বৈত হয় তবে লজিক্যাল রিগ্রেশন ব্যবহার করুন! যাইহোক, আমাদের প্রক্রিয়াকরণে যত বেশি বিকল্প রয়েছে, সঠিকটি বেছে নেওয়া তত বেশি কঠিন। একই পরিস্থিতি রিগ্রেশন মডেলের ক্ষেত্রেও ঘটে।

  বহুবিধ রিগ্রেশন মডেলের ক্ষেত্রে, স্ব-পরিবর্তনশীল এবং কারণ-পরিবর্তনের ধরন, তথ্যের মাত্রা এবং তথ্যের অন্যান্য মৌলিক বৈশিষ্ট্যগুলির উপর ভিত্তি করে সবচেয়ে উপযুক্ত প্রযুক্তি নির্বাচন করা অত্যন্ত গুরুত্বপূর্ণ। নিম্নলিখিতগুলি হল সঠিক রিগ্রেশন মডেল নির্বাচন করার জন্য আপনার মূল কারণঃ

  ডেটা এক্সপ্লোরেশন একটি ভবিষ্যদ্বাণীমূলক মডেল নির্মাণের একটি অপরিহার্য অংশ। এটি একটি উপযুক্ত মডেল নির্বাচন করার জন্য একটি অগ্রাধিকার পদক্ষেপ হওয়া উচিত, যেমন পরিবর্তনশীল সম্পর্ক এবং প্রভাব সনাক্তকরণ।

  তুলনা বিভিন্ন মডেলের জন্য উপযুক্ত, আমরা বিভিন্ন নির্দেশক প্যারামিটার বিশ্লেষণ করতে পারি যেমন পরিসংখ্যানগতভাবে গুরুত্বপূর্ণ প্যারামিটার, R-square, Adjusted R-square, AIC, BIC এবং ত্রুটি পয়েন্ট, অন্যটি হল Mallows’ Cp কমান্ড। এটি মূলত মডেলটিকে সমস্ত সম্ভাব্য উপ-মডেলের সাথে তুলনা করে (বা তাদের সাবধানে নির্বাচন করে) এবং আপনার মডেলের মধ্যে যে কোনও বিচ্যুতি হতে পারে তা পরীক্ষা করে।

  ক্রস-ভ্যালিডেশন হল ভবিষ্যদ্বাণীমূলক মডেলের মূল্যায়নের সবচেয়ে ভালো পদ্ধতি। এখানে, আপনার ডেটা সেটকে দুটি অংশে বিভক্ত করুন (একটি প্রশিক্ষণের জন্য এবং অন্যটি যাচাই করার জন্য) । আপনার ভবিষ্যদ্বাণী সঠিকতা পরিমাপ করার জন্য পর্যবেক্ষণের মান এবং ভবিষ্যদ্বাণী মানের মধ্যে একটি সহজ সমান্তরাল পার্থক্য ব্যবহার করুন।

  যদি আপনার ডেটাসেটটি একাধিক মিশ্র ভেরিয়েবল থাকে তবে আপনাকে স্বয়ংক্রিয় মডেল নির্বাচন পদ্ধতিটি বেছে নেওয়া উচিত নয়, কারণ আপনি একই সময়ে সমস্ত ভেরিয়েবলকে একই মডেলের মধ্যে রাখতে চান না।

  এটি আপনার উদ্দেশ্যের উপরও নির্ভর করবে। এমন পরিস্থিতি হতে পারে যেখানে একটি কম শক্তিশালী মডেল উচ্চ পরিসংখ্যানগত অর্থের মডেলের তুলনায় বাস্তবায়ন করা সহজ।

  রিগ্রেশন রুলারাইজেশন পদ্ধতি ((লাসো, রিজ এবং ইলাস্টিকনেট) উচ্চ মাত্রা এবং ডেটাসেট ভেরিয়েবলের মধ্যে একাধিক সহস্রাব্দতার ক্ষেত্রে ভাল কাজ করে।

সিএসডিএন থেকে পুনর্নির্দেশিত