নিষ্পাপ বেইসের আকর্ষণীয় উপলব্ধি

NavieBayes

  জীবনের অনেক ক্ষেত্রে শ্রেণিবদ্ধকরণ ব্যবহার করা প্রয়োজন, যেমন সংবাদ শ্রেণিবদ্ধকরণ, রোগী শ্রেণিবদ্ধকরণ ইত্যাদি বাস্তব ব্যবহারের দৃশ্য। এই নিবন্ধটি একটি সাধারণ সাধারণ শ্রেণিবদ্ধকরণ অ্যালগরিদমের সাথে পরিচয় করিয়ে দেয় যা ব্যবহারিক প্রয়োগ থেকে শুরু করে।

• 01 রোগীর শ্রেণীবিভাগের উদাহরণ

আমি একটি উদাহরণ দিয়ে শুরু করব, আপনি দেখতে পাবেন যে Bayes classifier খুব সহজেই বোঝা যায়, খুব কঠিন নয়। একটি হাসপাতাল সকালে ৬ জন রোগীকে ভর্তি করেছে, নিচের টেবিলে দেখানো হয়েছে।

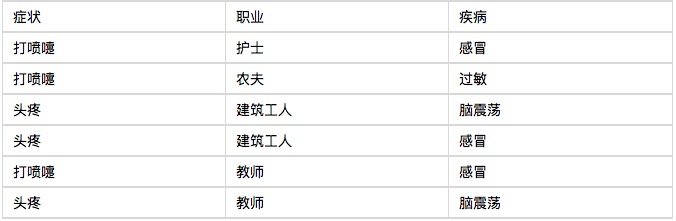
এখন সপ্তম রোগীর কথা বলা যাক, একজন নির্মাণ শ্রমিক যিনি হাঁচি খাচ্ছেন। তাকে জিজ্ঞেস করুন, তার ঠান্ডা লাগার সম্ভাবনা কতটুকু?

  P(A|B) = P(B|A) P(A) / P(B)

কিউবাঃ

  P(感冒|打喷嚏x建筑工人) 
  　　　　= P(打喷嚏x建筑工人|感冒) x P(感冒) 
  　　　　/ P(打喷嚏x建筑工人)

“Sneezing” এবং “Building Worker” এই দুটি বৈশিষ্ট্যকে স্বাধীন বলে ধরে নিলে, উপরের সমীকরণটি

  P(感冒|打喷嚏x建筑工人) 
  　　　　= P(打喷嚏|感冒) x P(建筑工人|感冒) x P(感冒)
  　　　　/ P(打喷嚏) x P(建筑工人)

এটা গণনা করা যায়।

  P(感冒|打喷嚏x建筑工人) 
  　　　　= 0.66 x 0.33 x 0.5 / 0.5 x 0.33 
  　　　　= 0.66

তাই, এই নির্মাতা, যিনি হাঁচি দেন, তার ৬৬% সম্ভাবনা রয়েছে যে তিনি একটি ঠান্ডা পেয়েছেন। একইভাবে, এই রোগীর অ্যালার্জি বা মস্তিষ্কের কম্পনের সম্ভাবনা গণনা করা যেতে পারে। এই সম্ভাবনার তুলনা করা হলে, আপনি জানতে পারবেন যে তিনি কোন রোগে আক্রান্ত হতে পারেন।

বেয়েস শ্রেণীবিভাগের মৌলিক পদ্ধতিটি হল: পরিসংখ্যানের উপর ভিত্তি করে, নির্দিষ্ট বৈশিষ্ট্যগুলির উপর ভিত্তি করে, বিভিন্ন শ্রেণীর সম্ভাব্যতা গণনা করা হয়, যার ফলে শ্রেণীবিন্যাস করা যায়।

• 02 সরল বেয়েজ শ্রেণীকরণকারীর সূত্র

অনুমান করা যাক যে কোনও ব্যক্তির n টি বৈশিষ্ট্য রয়েছে, যথাক্রমে F1, F2, … এবং Fn। বিদ্যমান m টি বিভাগ রয়েছে, যথাক্রমে C1, C2, … এবং Cm। বেয়েজ শ্রেণিবিন্যাসকারী হ’ল শ্রেণিবিন্যাস যা সর্বাধিক সম্ভাব্যতা গণনা করে, যা নিম্নলিখিত অ্যালগরিদমের সর্বাধিক মানঃ

  P(C|F1F2...Fn) 
  　　   = P(F1F2...Fn|C)P(C) / P(F1F2...Fn)

যেহেতু P ((F1F2…Fn) সকল শ্রেণীর জন্য একই, এটা বাদ দেওয়া যেতে পারে, এবং প্রশ্নটি পরিণত হয়

  P(F1F2...Fn|C)P(C)

এর সর্বোচ্চ মান

সাধারণ বেয়েজ শ্রেণিবিন্যাসকারী আরও এগিয়ে যায় এবং অনুমান করে যে সমস্ত বৈশিষ্ট্য একে অপরের থেকে স্বাধীন, এবং তাই

  P(F1F2...Fn|C)P(C) 
  　　   = P(F1|C)P(F2|C) ... P(Fn|C)P(C)

উপরের সমীকরণের ডানদিকে থাকা প্রত্যেকটি পদকে পরিসংখ্যান থেকে পাওয়া যায়, যার ফলে প্রতিটি শ্রেণীর সম্ভাব্যতা গণনা করা যায়, যার ফলে সর্বোচ্চ সম্ভাব্যতার শ্রেণীটি পাওয়া যায়।

যদিও “সমস্ত বৈশিষ্ট্য একে অপরের থেকে পৃথক” অনুমানটি বাস্তবে কার্যকর হওয়ার সম্ভাবনা কম, তবে এটি গণনাকে অনেক সহজ করে তোলে এবং গবেষণায় শ্রেণিবদ্ধকরণের ফলাফলের নির্ভুলতার উপর সামান্য প্রভাব ফেলে বলে প্রমাণিত হয়েছে।

নীচে দুটি উদাহরণ দেওয়া হল, যা দেখায় কিভাবে সরল বেয়েজ শ্রেণীকরণকারী ব্যবহার করা যায়।

• 03 অ্যাকাউন্টের শ্রেণীবিভাগ

একটি কমিউনিটি সাইটের নমুনা পরিসংখ্যান অনুসারে, ১০,০০০ অ্যাকাউন্টের মধ্যে ৮৯% সত্যিকারের অ্যাকাউন্ট (C0 সেট করুন) এবং ১১% ভুয়া (C1) ।

  C0 = 0.89 C1 = 0.11

ধরুন, একটি অ্যাকাউন্টে নিম্নলিখিত তিনটি বৈশিষ্ট্য রয়েছে। F1: লগের সংখ্যা / নিবন্ধনের দিন F2: বন্ধু সংখ্যা/সাইন আপের দিন সংখ্যা F3: সত্যিকারের শিরোনাম ব্যবহার করা হবে কিনা (সত্যিকারের শিরোনাম 1 এবং অ-সত্যিকারের শিরোনাম 0) F1 = 0.1  F2 = 0.2  F3 = 0

এই অ্যাকাউন্টটি কি আসল অ্যাকাউন্ট নাকি ভুয়া অ্যাকাউন্ট? এটি একটি সরল বেয়েজ শ্রেণিবিন্যাসক ব্যবহার করে এবং নিম্নলিখিত গণনা ফর্মুলারটির মান নির্ণয় করে।

P(F1|C)P(F2|C)P(F3|C)P©

যদিও উপরের মানগুলি পরিসংখ্যান থেকে পাওয়া যায়, এখানে একটি সমস্যা রয়েছেঃ F1 এবং F2 ধারাবাহিক পরিবর্তনশীল, কোন নির্দিষ্ট মানের উপর ভিত্তি করে সম্ভাব্যতা গণনা করা উপযুক্ত নয়। একটি কৌশল হ’ল ধারাবাহিক মানকে বিচ্ছিন্ন মানে রূপান্তর করা, একটি ব্যবধানের সম্ভাব্যতা গণনা করা। যেমন F1 কে বিভাজন করা[0, 0.05]、(0.05, 0.2)、[[0.2, +∞] তিনটা বিভাগ, তারপর প্রতিটি বিভাগের সম্ভাব্যতা গণনা করুন। আমাদের উদাহরণে, F1 হল 0.1, দ্বিতীয় বিভাগে পড়ে, তাই গণনা করার সময়, দ্বিতীয় বিভাগের ঘটনার সম্ভাব্যতা ব্যবহার করুন।

পরিসংখ্যান বলছেঃ

P(F1|C0) = 0.5, P(F1|C1) = 0.1  P(F2|C0) = 0.7, P(F2|C1) = 0.2  P(F3|C0) = 0.2, P(F3|C1) = 0.9

তাই

P(F1|C0) P(F2|C0) P(F3|C0) P(C0)  = 0.5 x 0.7 x 0.2 x 0.89  = 0.0623 P(F1|C1) P(F2|C1) P(F3|C1) P(C1)  = 0.1 x 0.2 x 0.9 x 0.11  = 0.00198 আপনি দেখতে পাচ্ছেন যে এই ব্যবহারকারীর আসল ছবি না থাকলেও, তার আসল অ্যাকাউন্টের সম্ভাবনা ভুয়া অ্যাকাউন্টের চেয়ে ৩০ গুণ বেশি, তাই এই অ্যাকাউন্টটি সত্য বলে বিবেচিত হয়েছে।

• 04 লিঙ্গ শ্রেণিবিন্যাস

নীচে মানব দেহের বৈশিষ্ট্যগুলির একটি গ্রুপের পরিসংখ্যান দেওয়া হল।

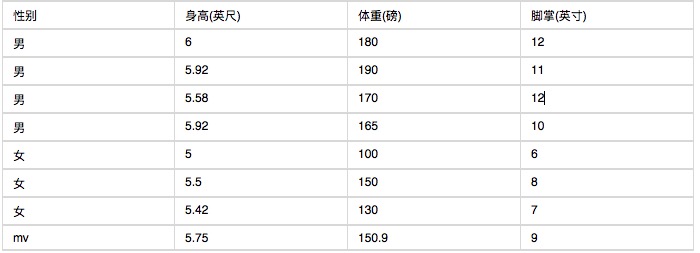
একটি ব্যক্তির উচ্চতা ৬ ফুট, ওজন ১৩০ পাউন্ড, পায়ের পাতা ৮ ইঞ্চি, দয়া করে জিজ্ঞাসা করুন তিনি পুরুষ নাকি মহিলা? নিচের ফর্মুলারটির মান নির্বিঘ্নে বেয়েজ শ্রেণিবিন্যাসকারী অনুসারে গণনা করুন।

P (উচ্চতা ও লিঙ্গ) x P (ওজন ও লিঙ্গ) x P (পা ও হাতের লিঙ্গ) x P (লিঙ্গ)

এখানে সমস্যা হল যে, উচ্চতা, ওজন এবং হাতের তালু ধারাবাহিক ভেরিয়েবল, তাই বিচ্ছিন্ন ভেরিয়েবলের পদ্ধতি ব্যবহার করা সম্ভব নয়। এবং যেহেতু নমুনা খুব কম, তাই এটি একটি ব্যবধানের মধ্যে গণনা করা সম্ভব নয়। তাহলে কি হবে? এই ক্ষেত্রে, আমরা অনুমান করতে পারি যে পুরুষ এবং মহিলাদের উচ্চতা, ওজন এবং হাতের তালু সঠিকভাবে বিতরণ করা হয়, এবং নমুনা থেকে গড় এবং ডিফারেনশিয়াল গণনা করা হয়, যা সঠিকভাবে বিতরণ করা হয় ঘনত্ব ফাংশন। ঘনত্ব ফাংশন আছে, আপনি একটি নির্দিষ্ট বিন্দুতে ঘনত্ব ফাংশনের মান গণনা করতে পারেন। উদাহরণস্বরূপ, পুরুষের উচ্চতা 5.855 হয়, এবং ডিফারেনশিয়াল 0.035 এর সঠিক বিতরণ। সুতরাং, পুরুষের উচ্চতা 6 ইঞ্চি স্কেল সম্ভাব্যতার তুলনামূলক মান 1.5789 ((( 1 এর চেয়ে বড় কোন সম্পর্ক নেই, কারণ এখানে ঘনত্ব ফাংশনের মানগুলি কেবলমাত্র পৃথক সম্ভাব্যতার তুলনামূলক মানকে প্রতিফলিত করে) ।

এই তথ্যের সাহায্যে লিঙ্গের ভিত্তিতে শ্রেণিবিন্যাস করা যায়।

P (উচ্চতা = 6 পুরুষ) x P (ওজন = 130 পুরুষ) x P (পা = 8 পুরুষ) x P (পুরুষ)

= 6.1984 x e-9

P (উচ্চতা = 6 ডগলাস মহিলা) x P (ওজন = 130 ডগলাস মহিলা) x P (পা = 8 ডগলাস মহিলা) x P (মহিলা)

= 5.3778 x e-4

আপনি দেখতে পাচ্ছেন যে, পুরুষদের তুলনায় মহিলাদের প্রায় ১০,০০০ গুণ বেশি সম্ভাবনা রয়েছে, তাই এই ব্যক্তিকে একজন মহিলা হিসেবে চিহ্নিত করুন।

উইকিপিডিয়ার সর্বজনীন নাম্বার থেকে উদ্ধৃত