লুকানো মার্কভ মডেল

• ### ১, পরিচয়

আজকে আমরা শেয়ার বাজারে এইচএমএম (HMM) এর সহজ প্রয়োগ সম্পর্কে জানবো।

ম্যালকভের মডেল, যা প্রথম দেখায় উচ্চমানের বলে মনে হচ্ছে, কিন্তু আমরা জানি না এটি কি, তাই আসুন আমরা এক ধাপ পিছনে যাই এবং ম্যালকভের চেইনটি দেখি।

মার্কভ চেইন, যা আন্দ্রে মার্কভের নামানুসারে নামকরণ করা হয়, গণিতে মার্কভীয় প্রকৃতির একটি বিচ্ছিন্ন ঘটনা-র্যান্ডম প্রক্রিয়াকে বোঝায়। বর্তমান জ্ঞান বা তথ্যের ক্ষেত্রে, অতীত (অর্থাৎ বর্তমানের পূর্ববর্তী ঐতিহাসিক অবস্থা) ভবিষ্যতের ভবিষ্যদ্বাণী করার জন্য অপ্রাসঙ্গিক (অর্থাৎ বর্তমানের পরবর্তী ভবিষ্যৎ অবস্থা) ।

এই প্রক্রিয়ার মধ্যে, প্রতিটি রাষ্ট্রের স্থানান্তর শুধুমাত্র পূর্ববর্তী n রাষ্ট্রের উপর নির্ভর করে। এই প্রক্রিয়াটি 1n-স্তরের মডেল হিসাবে পরিচিত, যেখানে n হল স্থানান্তরিত রাষ্ট্রের প্রভাবের সংখ্যা। সবচেয়ে সহজ মারকভ প্রক্রিয়া হল এক স্তরের প্রক্রিয়া, যেখানে প্রতিটি রাষ্ট্রের স্থানান্তর কেবল তার পূর্ববর্তী রাষ্ট্রের উপর নির্ভর করে।

• ### দ্বিতীয় উদাহরণ

গাণিতিকভাবে, এটি নিম্নরূপঃ

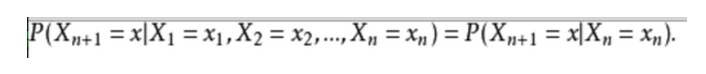
একটি দৈনন্দিন জীবনের উদাহরণ, আমরা বর্তমান আবহাওয়ার উপর ভিত্তি করে ভবিষ্যতের আবহাওয়ার ভবিষ্যদ্বাণী করতে চাই। একটি উপায় হল এই মডেলের প্রতিটি রাষ্ট্রকে শুধুমাত্র পূর্ববর্তী রাষ্ট্রের উপর নির্ভরশীল বলে ধরে নেওয়া, যা মার্কভের অনুমান, যা এই সমস্যাটিকে ব্যাপকভাবে সরল করে তোলে। অবশ্যই, এই উদাহরণটি কিছুটা অকার্যকরও। তবে, এই ধরনের একটি সরলীকৃত সিস্টেম আমাদের বিশ্লেষণে উপকারী হতে পারে, তাই আমরা সাধারণত এই ধরনের অনুমানগুলি গ্রহণ করি কারণ আমরা জানি যে এই ধরনের সিস্টেম আমাদের কিছু দরকারী তথ্য দেয়, যদিও খুব সঠিক নয়।

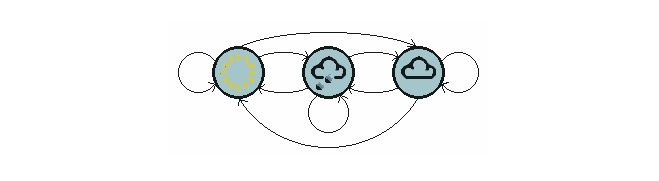
উপরের চিত্রটি একটি আবহাওয়ার স্থানান্তর মডেল দেখায়।

লক্ষ্য করুন যে একটি এক-স্তরীয় প্রক্রিয়া যা N স্টেট ধারণ করে তার N2 স্টেট ট্রান্সফার রয়েছে। প্রতিটি ট্রান্সফারের সম্ভাব্যতাকে স্টেট ট্রান্সফার সম্ভাব্যতা বলা হয়, যা এক স্টেট থেকে অন্য স্টেটে স্থানান্তরিত হওয়ার সম্ভাবনা। এই সমস্ত N2 সম্ভাব্যতাকে একটি স্টেট ট্রান্সফার ম্যাট্রিক্স দ্বারা উপস্থাপন করা যেতে পারে, উপরের আবহাওয়ার উদাহরণে স্টেট ট্রান্সফার ম্যাট্রিক্সটি নিম্নরূপঃ

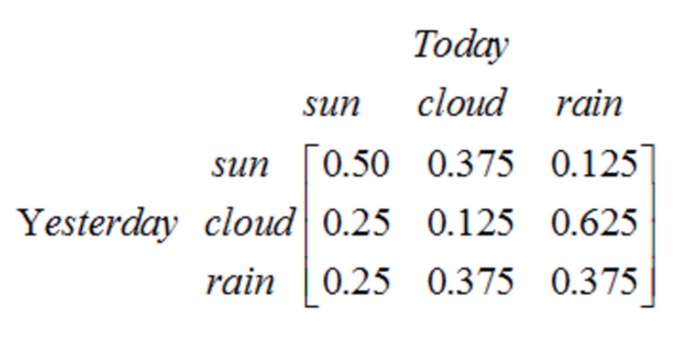
এই ম্যাট্রিক্সটি বলে যে, যদি গতকাল মেঘলা ছিল, তাহলে আজ 25% সম্ভাবনা রয়েছে যে, দিনটি পরিষ্কার থাকবে, 12.5% সম্ভাবনা রয়েছে যে, দিনটি মেঘলা থাকবে, 62.5% সম্ভাবনা রয়েছে যে, বৃষ্টি হবে, এবং স্পষ্টতই, ম্যাট্রিক্সের প্রতিটি লাইনের যোগফল হবে 1 ।

এই ধরনের একটি সিস্টেমকে প্রাথমিকীকরণ করার জন্য, আমাদের একটি প্রাথমিক সম্ভাব্যতা ভেক্টর প্রয়োজনঃ

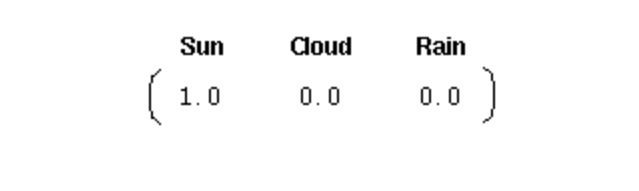
এই ভেক্টরটি প্রথম দিনকে একটি উজ্জ্বল দিন বলে। এখানে, আমরা উপরের এক স্তরের মার্কভ প্রক্রিয়াটির জন্য নিম্নলিখিত তিনটি অংশ সংজ্ঞায়িত করেছিঃ

মেঘলা আবহাওয়ার মধ্যে বৃষ্টিপাতের সম্ভাবনা রয়েছে।

প্রাথমিক ভেক্টরঃ সিস্টেমের অবস্থা নির্ধারণের সম্ভাবনা যখন সময় 0 হয়।

অবস্থা স্থানান্তর ম্যাট্রিক্সঃ প্রতিটি আবহাওয়ার পরিবর্তনের সম্ভাবনা। সমস্ত সিস্টেম যা এইভাবে বর্ণনা করা যায় তা একটি মার্কভ প্রক্রিয়া।

যাইহোক, যখন মার্কভ প্রক্রিয়া যথেষ্ট শক্তিশালী নয়, তখন আমরা কী করব? কিছু ক্ষেত্রে, মার্কভ প্রক্রিয়াটি এমন একটি মডেলকে বর্ণনা করতে যথেষ্ট নয় যা আমরা আশা করি।

উদাহরণস্বরূপ, আমাদের শেয়ার বাজার, যদি আমরা কেবল বাজারের পর্যবেক্ষণ করি, তবে আমরা কেবল সেই দিনের দাম, লেনদেনের পরিমাণ ইত্যাদি তথ্য জানতে পারি, তবে শেয়ার বাজারটি বর্তমানে কী অবস্থায় রয়েছে তা আমরা জানি না ((বুল বাজার, বেয়ার বাজার, ঝাঁকুনি, বিপর্যয় ইত্যাদি) । এই ক্ষেত্রে আমাদের দুটি রাষ্ট্রের সংগ্রহ রয়েছে, একটি পর্যবেক্ষণযোগ্য রাষ্ট্রের সংগ্রহ ((শেয়ার বাজার মূল্য লেনদেনের অবস্থা ইত্যাদি) এবং একটি লুকানো রাষ্ট্রের সংগ্রহ ((শেয়ার বাজার পরিস্থিতি) । আমরা আশা করি এমন একটি অ্যালগরিদম খুঁজে পাব যা শেয়ার বাজার এবং মারকভের অনুমানের উপর ভিত্তি করে শেয়ার বাজারগুলির অবস্থা পূর্বাভাস দিতে পারে।

উপরোক্ত ক্ষেত্রে, পর্যবেক্ষণযোগ্য এবং লুকানো ধারাবাহিকতার ধারাবাহিকতা সম্ভাব্যতার সাথে সম্পর্কিত। সুতরাং আমরা এই ধরনের প্রক্রিয়াটিকে একটি লুকানো মার্কভ প্রক্রিয়া এবং এই লুকানো মার্কভ প্রক্রিয়াটির সম্ভাব্যতার সাথে সম্পর্কিত এবং পর্যবেক্ষণযোগ্য অবস্থার একটি সেট হিসাবে মডেল করতে পারি, যা লুকানো মার্কভ মডেল।

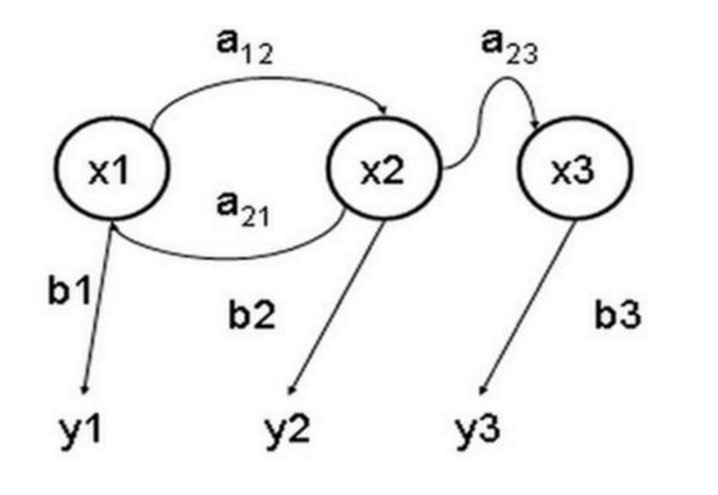
একটি লুকানো মার্কভ মডেল হল একটি পরিসংখ্যানগত মডেল যা একটি মার্কভ প্রক্রিয়া বর্ণনা করে যার মধ্যে লুকানো অজানা প্যারামিটার রয়েছে। এর অসুবিধা হল যে প্রক্রিয়াটির লুকানো প্যারামিটারগুলি পর্যবেক্ষণযোগ্য প্যারামিটারগুলি থেকে সনাক্ত করা হয়, তারপরে এই প্যারামিটারগুলিকে আরও বিশ্লেষণের জন্য ব্যবহার করা হয়। নীচের চিত্রটি একটি তিন-স্টেট লুকানো মার্কভ মডেলের অবস্থা স্থানান্তর চিত্র, যেখানে x লুকানো অবস্থা, y পর্যবেক্ষণযোগ্য আউটপুট, a রাষ্ট্র রূপান্তর সম্ভাবনা, এবং b আউটপুট সম্ভাবনা।

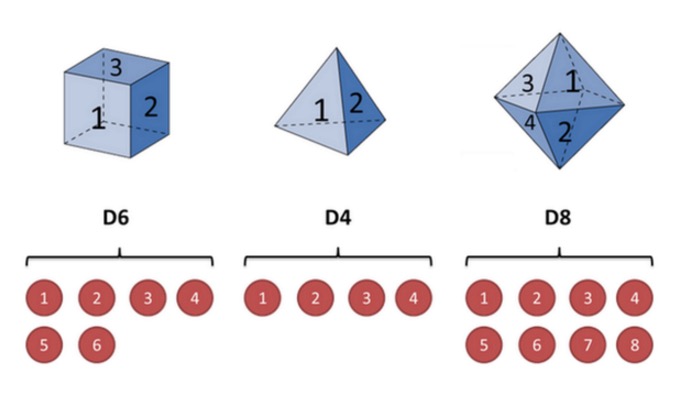
একটি ছুরি উদাহরণ দিয়ে ব্যাখ্যা করা যাকঃ ধরুন আমার হাতে তিনটি ভিন্ন ছুরি রয়েছে। প্রথম ছুরিটি আমাদের সাধারণ ছুরি (এই ছুরিটিকে D6 বলুন), যার 6 টি দিক রয়েছে, প্রতিটি দিকের (১,২,৩,৪,৫,৬) হওয়ার সম্ভাবনা 1/6। দ্বিতীয় ছুরিটি একটি চতুর্ভুজ (এই ছুরিটিকে D4 বলুন), প্রতিটি দিকের (১,২,৩,৪) হওয়ার সম্ভাবনা 1/4। তৃতীয় ছুরিটির আটটি দিক রয়েছে (এই ছুরিটিকে D8 বলুন) এবং প্রতিটি দিকের (১,২,৩,৪,৫,৬,৭,৮) হওয়ার সম্ভাবনা 1/8।

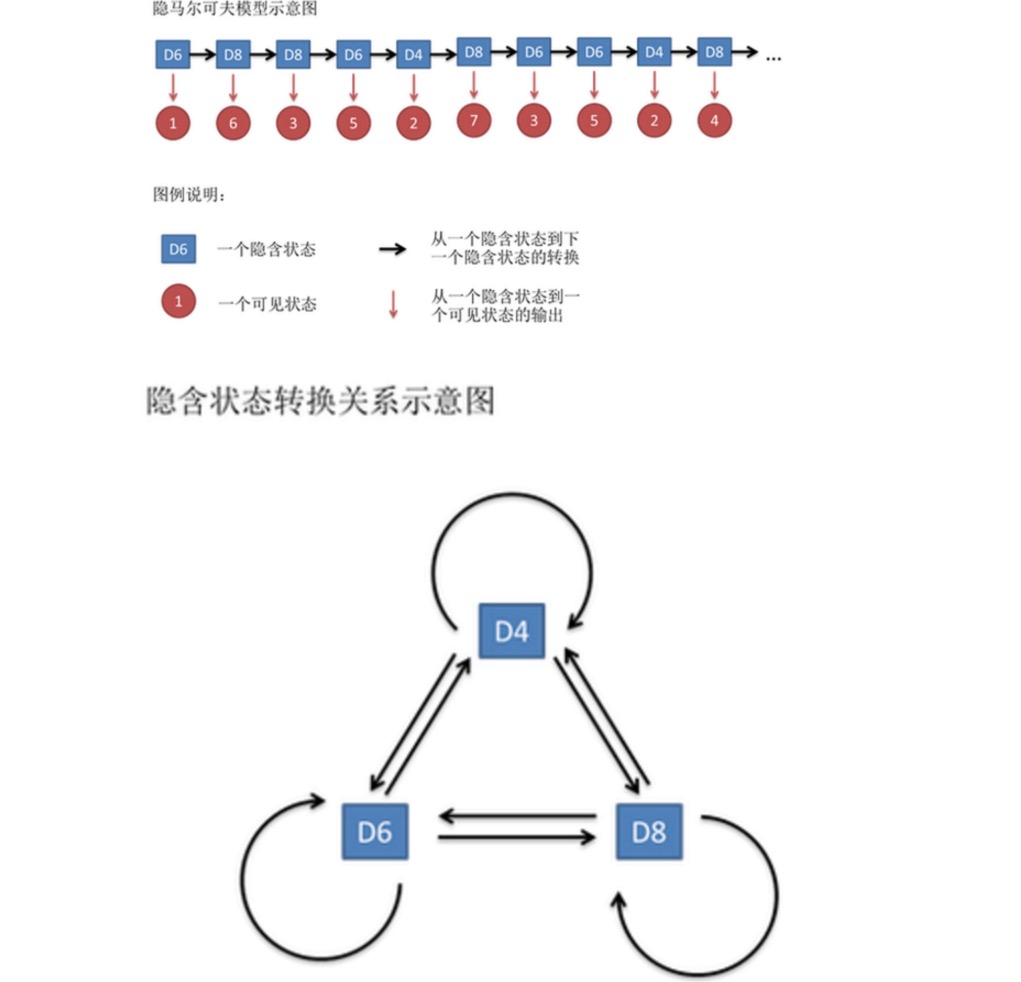
ধরুন, আমরা একটি বাটি শুরু করি, আমরা তিনটি বাটি থেকে একটি বাটি বেছে নিই, এবং প্রতিটি বাটি বেছে নেওয়ার সম্ভাব্যতা 1/3। তারপর আমরা একটি বাটি বেছে নিই, এবং আমরা একটি সংখ্যা পাই, 1, 2, 3, 4, 5, 6, 7, 8 এর মধ্যে একটি। এই প্রক্রিয়াটি বারবার পুনরাবৃত্তি করে, আমরা একটি সংখ্যা পাই, এবং প্রতিটি সংখ্যা 1, 2, 3, 4, 5, 6, 7, 8 এর মধ্যে একটি। উদাহরণস্বরূপ, আমরা একটি সংখ্যা পেতে পারি (বাটি 10 বার): 1 6 3 5 2 7 3 5 2 4

এই ক্রমকে বলা হয় দৃশ্যমান অবস্থা চেইন। কিন্তু ইনকুইন মারকভ মডেলের ক্ষেত্রে, আমরা শুধু এই দৃশ্যমান অবস্থা চেইনই পাই না, আমরা একটি ইনকুইন অবস্থা চেইনও পাই। এই উদাহরণে, এই ইনকুইন অবস্থা চেইনটি হল আপনার ব্যবহৃত ছুরিগুলির ক্রম। উদাহরণস্বরূপ, ইনকুইন অবস্থা চেইনটি হতে পারেঃ D4 D6 D8 D6 D4 D8 D6 D6 D4।

সাধারণভাবে, এইচএমএম-তে বলা মারকভ চেইন আসলে অন্তর্নিহিত রাষ্ট্রের চেইনকে বোঝায়, কারণ অন্তর্নিহিত রাষ্ট্রের মধ্যে রূপান্তর সম্ভাবনা রয়েছে। আমাদের উদাহরণে, D6 এর পরবর্তী রাষ্ট্রটি D4, D6, D8 এর সম্ভাবনা 1/3। D4, D8 এর পরবর্তী রাষ্ট্রটি D4, D6, D8 এর রূপান্তর সম্ভাবনাও 1/3। এইভাবে সেট করা শুরু করার জন্য সহজ, তবে আমরা আসলে রূপান্তর সম্ভাবনাটি নির্বিচারে সেট করতে পারি। উদাহরণস্বরূপ, আমরা এইভাবে সংজ্ঞায়িত করতে পারি যে D6 এর পরে D4, D6 এর পরে D6 এর সম্ভাবনা 0.9, D8 এর সম্ভাবনা 0.1।

একইভাবে, যদিও দৃশ্যমান অবস্থার মধ্যে রূপান্তর হওয়ার সম্ভাবনা নেই, তবে অন্তর্নিহিত অবস্থা এবং দৃশ্যমান অবস্থার মধ্যে একটি সম্ভাবনা রয়েছে যা আউটপুট সম্ভাবনা বলা হয়। আমাদের উদাহরণে, ষড়ভুজ ((D6) 1 এর আউটপুট সম্ভাবনা 1/6। 2, 3, 4, 5, 6 এর সম্ভাবনাও 1/6। আমরা একইভাবে আউটপুট সম্ভাব্যতার অন্যান্য সংজ্ঞাগুলিও করতে পারি। উদাহরণস্বরূপ, আমার কাছে একটি ক্যাসিনো দ্বারা চালিত ষড়ভুজ রয়েছে যা 1 এর সম্ভাবনা বেশি, ¹⁄₂, 2, 3, 4, 5, 6 এর সম্ভাবনা 1/10।

আসলে, এইচএমএম এর ক্ষেত্রে, যদি আপনি সমস্ত লুকানো রাজ্যের মধ্যে রূপান্তর সম্ভাব্যতা এবং সমস্ত লুকানো রাজ্যের মধ্যে সমস্ত দৃশ্যমান রাজ্যের মধ্যে আউটপুট সম্ভাব্যতা আগে থেকেই জানেন তবে সিমুলেশন করা বেশ সহজ। তবে এইচএমএম মডেলটি প্রয়োগ করার সময়, প্রায়শই কিছু তথ্য অনুপস্থিত থাকে। কখনও কখনও আপনি জানেন যে কয়টি প্রজাপতি রয়েছে এবং প্রতিটি প্রজাপতি কী, তবে আপনি জানেন না যে প্রজাপতির ক্রমটি বেরিয়ে এসেছে; কখনও কখনও আপনি কেবল প্রজাপতির ফলাফলটি অনেকবার দেখেছেন এবং বাকি কিছুই জানেন না। যদি অ্যালগরিদমগুলি এই অনুপস্থিত তথ্যের অনুমান করতে প্রয়োগ করা হয় তবে এটি একটি গুরুত্বপূর্ণ সমস্যা হয়ে দাঁড়িয়েছে।

এইচএমএম মডেলের সাথে সম্পর্কিত অ্যালগরিদমগুলি মূলত তিনটি বিভাগে বিভক্ত এবং তিনটি সমস্যা সমাধান করেঃ

• আমি জানতে চাই যে কতগুলি প্রজাপতি রয়েছে ((অন্তর্নিহিত রাষ্ট্রের সংখ্যা), প্রতিটি প্রজাপতি কী ((রূপান্তর সম্ভাবনা), প্রজাপতিটি যে ফলাফলটি বের করেছে তার উপর ভিত্তি করে ((দৃশ্যমান রাষ্ট্রের চেইন), আমি জানতে চাই যে প্রতিটি প্রজাপতি কোন প্রজাপতিটি বের করেছে ((অন্তর্নিহিত রাষ্ট্রের চেইন)) ।

• আমি জানতে চাচ্ছি যে কতগুলি কয়েন রয়েছে (অন্তর্নিহিত রাষ্ট্রের সংখ্যা), প্রতিটি কয়েন কি (রূপান্তরের সম্ভাবনা), কয়েন থেকে প্রাপ্ত ফলাফলের উপর ভিত্তি করে (দৃশ্যমান রাষ্ট্র শৃঙ্খলা), আমি জানতে চাই যে এই ফলাফলটি প্রাপ্ত হওয়ার সম্ভাবনা কী।

• আমি জানি যে কতগুলি প্রজাপতি রয়েছে (অন্তর্নিহিত অবস্থার সংখ্যা), আমি জানি না যে প্রতিটি প্রজাপতি কী (রূপান্তরের সম্ভাবনা), আমি অনেকবার প্রজাপতির ফলাফল পর্যবেক্ষণ করেছি (দৃশ্যমান অবস্থা চেইন), আমি পুনরাবৃত্তি করতে চাই যে প্রতিটি প্রজাপতি কী (রূপান্তরের সম্ভাবনা) ।

  যদি আমরা শেয়ারবাজারের সমস্যা সমাধান করতে চাই, তাহলে আমাদের প্রথম এবং তৃতীয় প্রশ্নের সমাধান করতে হবে। পরবর্তী নিবন্ধে আমরা দেখব কিভাবে এটা করা যায়।

“মনিকোড” থেকে পুনর্নির্দেশিত