৫) বেয়েস, একজন মানুষ যিনি কেবল শিক্ষামূলক উপকরণে বাস করেন

** জন্মসূত্রে নামহীন বেয়েস এর কাজ একদিকে এই উত্তেজনাপূর্ণ ধারণার প্রমাণ অব্যাহত রেখেছে যে অস্থিরতা একটি পরিমাপযোগ্য শক্তি, অন্যদিকে আমাদেরকে একটি উপায় প্রদান করে যা আমাদের দ্বারা প্রাপ্ত তথ্যের উপর ভিত্তি করে অজানা সম্ভাবনার অনুমান করার জন্য, যা আমাদের দ্বারা প্রাপ্ত তথ্যের উপর ভিত্তি করে।

** টমাস বেয়েস এর মতো একজন ব্যক্তি যিনি পুরো বিজ্ঞানের ইতিহাসে বিখ্যাত হয়ে উঠেছেন, তার ব্যক্তিগত জীবনের গল্প লেখার মতো কিছুই নেই, এটি একটি খুব অদ্ভুত বিষয়। এই দিকটি বেয়েস এর জীবনকালের আগে সত্যই খুব নিচু ছিল (অথবা, এটি অ-লাল) । অন্যদিকে, আমার মতো লেখকের পক্ষে এটি খুব বড় অসুবিধার কারণ, কারণ বাস্তবে সবাই বিজ্ঞানীদের অদ্ভুত ঘটনাগুলি দেখতে পছন্দ করে, যেমন দুর্বল যোগাযোগের পাশাপাশি উন্মাদতা, যেমন খেলনা হতাশার বিরতি বিরতি বিস্ময়কর, আর অসুবিধাটি হ’ল ডাইফ্লাইডের সাথে সম্পর্কযুক্ত হতে পারে তবে গবেষণা করতে আগ্রহী নয়, অন্যথায় এটি সম্পূর্ণরূপে প্রতিভার বৈশিষ্ট্যকে প্রতিফলিত করতে পারে না।**

• টমাস বেয়েস তবে বেয়েস এমন এক বিরক্তিকর ব্যক্তি ছিলেন। তিনি ছিলেন একটি অ-প্রধানধারার ধর্মীয় যাজক যিনি ইংল্যান্ডের গ্রামাঞ্চলে বাস করতেন এবং তার কাজ ছিল সম্ভবত পুরো গ্রামকে একসাথে স্কয়ার ডান্সের আয়োজন করা, না, মিসেস, এবং বলা হয় যে পুরো গ্রামটি তাকে খুব পছন্দ করত। একমাত্র যা কিছুটা কিংবদন্তি বলে মনে হয় তা হ’ল তিনি অনেক কিংবদন্তির মতোই ছিলেন এবং জীবিতকালে একটি বই প্রকাশ করেননি। অবশ্যই বেশিরভাগ কিংবদন্তিও নন। এছাড়াও, বেয়েস সম্ভাব্যতা তত্ত্ব নিয়ে গবেষণা করার সিদ্ধান্ত নিয়েছিলেন কারণ তিনি Godশ্বরের অস্তিত্ব প্রমাণ করতে চেয়েছিলেন, তবে চূড়ান্ত গবেষণা এবং প্রভাবের কারণে, গির্জার অজানা লোকেরা তাকে বিশ্বাসঘাতক বলে মনে করবে না।

বেয়েস যখন মারা যান, তখন তিনি প্রিন্স নামে একজন ধর্মপ্রচারককে তার প্রবন্ধের পাণ্ডুলিপি ছাড়াও ১০০ পাউন্ড রেখে যান। এই প্রিন্সও একজন অদ্ভুত মানুষ ছিলেন, আধ্যাত্মিক সভ্যতা এবং উপাদান সভ্যতার নির্মাণ বেয়েস জানেন না যে তিনি কোথায় গিয়েছিলেন। তিনি মনে করেছিলেন যে মুক্ত ইচ্ছা divineশ্বরিক ছিল এবং আমেরিকার স্বাধীনতার প্রমাণও লিখেছিলেন God’sশ্বরের ইচ্ছা, বলা হয় যে ফ্র্যাংকলিন এবং অ্যাডামস্মি তার ভাল বন্ধু ছিলেন এবং তিনি অতিরিক্ত সময়ে বীমা সংস্থাগুলির জন্য ফি মডেলও করেছিলেন।

বেয়েসের মৃত্যুর তিন বছর পর, প্রিন্স তার উত্তরাধিকারী পত্রিকাটি প্রকাশ করতে সাহায্য করেন। কিন্তু এই পত্রিকার যুগ নির্ধারক তাৎপর্য একাডেমিক সম্প্রদায়ের দ্বারা অবহেলিত হয় এবং আরও দুই দশক অপেক্ষা করে। পত্রিকায়, বেয়েস এই প্রশ্নটি নিয়ে গবেষণা করতে চেয়েছিলেনঃ যদি আমরা কেবল একটি ঘটনার সংখ্যা জানি এবং এটি কতবার ঘটেনি, অন্য কোনও তথ্য না থাকলে আমরা কীভাবে এই ঘটনার সম্ভাবনা গণনা করব?

উদাহরণস্বরূপ, যদি আমরা 10,000 টি পণ্যের একটি ব্যাচের জন্য পরীক্ষা করে দেখি যে তাদের মধ্যে 12 টি বর্জ্য রয়েছে, তবে এই ব্যাচের জন্য বর্জ্যের হার 0.1% এর সম্ভাবনা কত? বাস্তব জীবনের জন্য, এই প্রশ্নটি অবশ্যই আমাদের জন্য আরও মূল্যবান, কারণ প্রত্যেকেরই জিনিসগুলির পর্যবেক্ষণের সর্বদা সীমাবদ্ধতা রয়েছে, আমাদের জানতে হবে যে আমরা যা দেখি তা কতটা সত্যকে প্রতিফলিত করতে পারে, ঠিক যেমন আমরা যদি স্পর্শ করি তবে কীভাবে আমরা নিশ্চিত হব যে আমরা পুরো হাতিটি স্পর্শ করছি বা বড় ভাইয়ের সাথে তুলনামূলকভাবে মোটা হয়েছি।

বেয়েস এর পদ্ধতি আসলে নতুন তথ্য দিয়ে পুরানো তথ্য সংশোধন করা, সংশোধনের উপর ভিত্তি করে সম্ভাবনার বিশ্বাসযোগ্যতা বাড়ানো। এটি কিংবদন্তি পূর্ববর্তী সম্ভাব্যতা এবং পরবর্তী সম্ভাব্যতা। এই বিষয়ে, বেয়েস তার গবেষণায় একটি ক্লাসিক উদাহরণ দিয়েছেনঃ

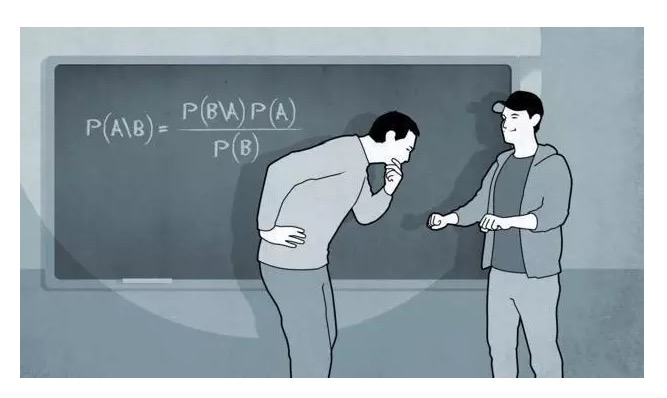
ধরুন, আমরা টেবিলে একটি বল খেলি এবং বলটি যে কোন স্থানে থেমে যায়। তারপর আমরা বারবার আরেকটি বল খেলি এবং গণনা করি যে এটি প্রথম বলের বাম এবং ডানদিকে কতবার ঘুরছে। অবশ্যই এখানে আপনি যুক্তিযুক্তভাবে প্রশ্ন করতে পারেন যে, যেহেতু আমরা টেনিস খেলতে যাচ্ছি, কেন দ্বিতীয় বলটি প্রথম বলটি খেলতে নয়, আমি মনে করি আপনি এই প্রশ্নটি খুব ভালভাবে জিজ্ঞাসা করেছেন, কিন্তু আমি উত্তর দিতে চাই না। সবশেষে আমরা দ্বিতীয় বলটি বাম এবং ডানদিকে কতবার উপস্থিত হতে পারি তার দ্বারা সরাসরি প্রথম বলের থামার সম্ভাব্যতা অনুমান করতে পারি।

এই দৃষ্টান্তে, প্রথম বলের অবস্থানের জন্য সরাসরি দেওয়া সম্ভাব্যতা হল প্রাথমিক সম্ভাব্যতা, এবং দ্বিতীয় বলের অবস্থার উপর ভিত্তি করে সিদ্ধান্ত নেওয়া প্রথম বলের অবস্থানের পরিবর্তনের সম্ভাব্যতা হল পরোক্ষ সম্ভাব্যতা। অর্থাৎ, বেয়েস পদ্ধতিটি হল যে আমাদের জ্ঞান আমাদের জ্ঞানীয় ক্ষমতার সীমাবদ্ধতা দ্বারা সীমাবদ্ধ, তাই আমাদের ক্রমাগত আপডেট হওয়া তথ্যের সাথে আমাদের মতামত সংশোধন করতে হবে। এবং দার্শনিক উচ্চতায় উঠে আসা, যে বিশ্বের উত্স সম্ভবত এলোমেলো নয়, তবে আমাদের ক্ষমতা আমাদের এই ধরনের উত্সকে চিনতে যথেষ্ট নয়, তাই আমরা কেবলমাত্র বিদ্যমান প্রমাণের উপর নির্ভর করে অনুমান করতে পারি, বা বলতে পারি, অনুমান করতে পারি।

উপরের এই বাক্যটি সম্ভবত সবচেয়ে জোরালো বাক্য, যা এই পর্যন্ত সংযুক্ত করা হয়েছে। আসুন আমরা একটি উদাহরণ দিয়ে ব্যাখ্যা করিঃ

আপনার শহরে দুটি শপিংমল খোলা হয়েছে, এবং নতুন শপিংমলের মোট ট্র্যাফিকের 60% লোকের ট্র্যাফিক রয়েছে, সুতরাং এই মুহুর্তে যে কোনও গ্রাহক শপিংমলের গ্রাহক হওয়ার 60% সম্ভাবনা রয়েছে। এটি পূর্ববর্তী সম্ভাবনা। এবং পুরানো শপিংমলের সুবিধাটি পরিচালনার জন্য পুরানো, কর্মীদের প্রশিক্ষণের স্তরও কম, অভিযোগের হার নতুন শপিংমলের দ্বিগুণ। এখন যদি কেউ শপিংমলের কাছে অভিযোগ পাঠায়, তাহলে শপিংমলের কোন পরিচালককে দায়ী করা উচিত?

সবচেয়ে সংক্ষিপ্ত এবং সুস্পষ্ট উত্তর হল যে সে সরাসরি এই ব্যক্তিকে জিজ্ঞাসা করে যে সে কোথায় ছিল। অবশ্যই সেই ব্যক্তি সম্ভবত উত্তর দেবে যে আপনি অনুমান করেছেন ((খুব খারাপ), তাহলে সে কীভাবে অনুমান করতে পারে যে তার সঠিক হওয়ার সম্ভাবনা বেশি? যদি পূর্বের সম্ভাব্যতা থেকে দেখা যায়, তবে সে নতুন মলের পরিচালককে খুঁজে পাবে, কারণ নতুন মলের মানুষের ট্র্যাফিক পুরানো মলের চেয়ে বেশি। তবে অভিযোগের দিক থেকে দেখা যায়, নতুন মলের অভিযোগের পরিমাণ মোট অভিযোগের মাত্র ১/৩ ভাগ। সুতরাং যদি আমরা এই তথ্যটি উল্লেখ করি তবে আমরা দেখতে পাব যে নতুন মলের অভিযোগের সম্ভাবনা ৪২.৮% এবং পুরানো মলের অভিযোগের সম্ভাবনা ৫৭.২%। এই ফলাফলটি, অর্থাৎ প্রাক্কলিক সম্ভাবনা, আমাদের বলে যে সে পুরানো মলের পরিচালককে খুঁজে পাওয়া উচিত।

জন্মসূত্রে নামহীন বেয়েস এখন প্রায় সমস্ত পরিসংখ্যান, কৃত্রিম বুদ্ধিমত্তা, গেম থিওরি এবং জেনেটিক্সের পাঠ্যপুস্তকে উপস্থিত রয়েছেন এবং অনেক কলেজের চূড়ান্ত পরীক্ষার পরীক্ষার্থীদের জীবনে অসংখ্য ঝামেলা সৃষ্টি করেছেন। তার কাজটি একদিকে প্রমাণ করে যে অনিশ্চয়তা একটি উত্তেজনাপূর্ণ ধারণা যা আমরা পরিমাপ করতে পারি, অন্যদিকে আমাদের কাছে একটি উপায় সরবরাহ করে যা আমাদের তথ্যের উপর ভিত্তি করে অজানা সম্ভাব্যতা অনুমান করতে পারে, যা আমাদের দ্বারা প্রাপ্ত তথ্যের উপর ভিত্তি করে ক্রমাগত সংশোধন করা হয়। এই ধারণার সাথে আমাদের ঝুঁকি পরিচালনার লক্ষ্য এবং অনুশীলনের সাথে দ্বন্দ্ব রয়েছেঃ একটি গতিশীল পরিবর্তিত বাজারে, যদি অনিশ্চয়তা থাকে তবে কোনও ফলাফল এবং সিদ্ধান্ত নেওয়া আমাদের সর্বশেষ এবং সর্বাধিক বিস্তৃত তথ্যের উপর নির্ভর করে, এবং এই ধরনের থামানো যুক্তিটি একই নয়।

চীনের কোয়ান্টাম ইনভেস্টমেন্ট অ্যাসোসিয়েশনের সৌজন্যে