পাইথন ন্যাইভ বেইস অ্যাপ্লিকেশন

বেয়েজ তত্ত্বের উপর ভিত্তি করে, বেয়েজ শ্রেণিবিন্যাসটি সহজতর করা যায়, যদি পূর্ববর্তী পরিবর্তনশীলগুলি একে অপরের থেকে পৃথক থাকে। আরও সহজভাবে বলতে গেলে, একটি বেয়েজ শ্রেণিবিন্যাসকারী একটি শ্রেণিবিন্যাসের বৈশিষ্ট্যগুলিকে এই শ্রেণিবিন্যাসের অন্যান্য বৈশিষ্ট্যগুলির সাথে সম্পর্কহীন বলে ধরে নেয়। উদাহরণস্বরূপ, যদি একটি ফল গোলাকার এবং লাল হয় এবং এর ব্যাস প্রায় 3 ইঞ্চি হয়, তবে ফলটি একটি আপেল হতে পারে। এমনকি যদি এই বৈশিষ্ট্যগুলি একে অপরের উপর নির্ভর করে বা অন্য বৈশিষ্ট্যগুলির উপর নির্ভর করে, তবে বেয়েজ শ্রেণিবিন্যাসকারী এই বৈশিষ্ট্যগুলিকে পৃথকভাবে ধরে নেবে যা ফলটিকে একটি আপেল বলে বোঝায়।

• #### সরল বেয়েজ মডেলগুলি তৈরি করা সহজ এবং বড় ডেটাসেটগুলির জন্য খুব কার্যকর। যদিও এটি সহজ, সরল বেয়েজ মডেলগুলি খুব জটিল শ্রেণিবদ্ধকরণ পদ্ধতির বাইরে চলে যায়।

বেয়েস সূত্রটি P © থেকে P (x) এবং P (x) থেকে P (x) এর সম্ভাব্যতা গণনা করার একটি উপায় প্রদান করে। নিম্নলিখিত সমীকরণটি দেখুনঃ

এখানে,

P © is the probability of the outcome of the class (objective), assuming that the predictor (property) is known P © হল শ্রেণীর প্রাথমিক সম্ভাবনা P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) P (x) হল পূর্বাভাস ভেরিয়েবলের পূর্ববর্তী সম্ভাবনা উদাহরণঃ চলুন আমরা একটি উদাহরণ দিয়ে এই ধারণাটি বুঝতে পারি। নীচে, আমার কাছে একটি আবহাওয়ার প্রশিক্ষণ সেট এবং এর সাথে সম্পর্কিত লক্ষ্য পরিবর্তনশীল Play আছে। এখন, আবহাওয়ার উপর নির্ভর করে আমাদের খেলোয়াড়দের খেলোয়াড় এবং খেলোয়াড়দের খেলোয়াড়দের মধ্যে শ্রেণিবদ্ধ করতে হবে। আসুন আমরা নিম্নলিখিত পদক্ষেপগুলি সম্পাদন করি

ধাপ ১ঃ ডাটা সেটকে ফ্রিকোয়েন্সি টেবিলে রূপান্তর করুন।

ধাপ ২ঃ একটি সম্ভাব্যতা টেবিল তৈরি করুন যেখানে একই ক্যাচটি 0.29 ওভারকাস্ট সম্ভাবনা সহ 0.64 ক্যাচ খেলার সম্ভাবনা রয়েছে।

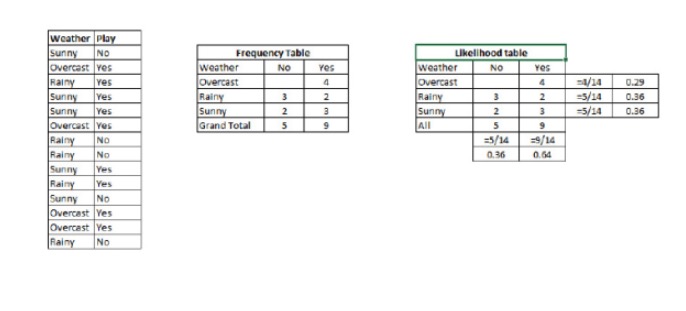
ধাপ ৩ঃ এখন, সাধারণ বেয়েজ সমীকরণ ব্যবহার করে প্রতিটি শ্রেণীর পরবর্তি সম্ভাব্যতা গণনা করুন। যে শ্রেণীর পরবর্তি সম্ভাব্যতা সবচেয়ে বেশি, সেই শ্রেণীর ফলাফলকে ভবিষ্যদ্বাণী করা হয়।

প্রশ্নঃ এই বিবৃতিটি কি সঠিক?

আমরা যে পদ্ধতিটি নিয়ে আলোচনা করেছি তা ব্যবহার করে আমরা এই সমস্যার সমাধান করতে পারি। সুতরাং P (খেলবে) = P (খেলবে) * P (খেলবে) / P (খেলবে)

আমরা P = ³⁄₉ = 0.33, P = ⁵⁄₁₄ = 0.36, P = ⁹⁄₁₄ = 0.64.

এখন, P{\displaystyle P} = 0.33 * 0.64 / 0.36 = 0.60, এবং এর সম্ভাবনা আরও বেশি।

সরল বেয়েস একটি অনুরূপ পদ্ধতি ব্যবহার করে বিভিন্ন শ্রেণীর সম্ভাব্যতা বিভিন্ন বৈশিষ্ট্য দ্বারা পূর্বাভাস দেয়। এই অ্যালগরিদমটি সাধারণত পাঠ্য শ্রেণিবদ্ধকরণ এবং একাধিক শ্রেণীর সাথে সম্পর্কিত সমস্যার জন্য ব্যবহৃত হয়।

• #### পাইথন কোডঃ

  #Import Library
  from sklearn.naive_bayes import GaussianNB
  　　
  #Assumed you have, X (predictor) and Y (target) for training data set and x_test(predictor) of test_dataset

Create SVM classification object model = GaussianNB()

there is other distribution for multinomial classes like Bernoulli Naive Bayes, Refer link

Train the model using the training sets and check score

model.fit(X, y) #Predict Output predicted= model.predict(x_test)