লিকস এবং বিড-আস্ক স্প্রেড: EKOP মডেলের উপর একটি প্রাথমিক গবেষণা

• ১ প্রারম্ভ

  সাম্প্রতিক সময়ে আমি অত্যন্ত ব্যস্ত, গত কয়েক মাস ধরে আমি আমার কলাম লিখে আসছি। এই কয়েক মাসে অনেক কিছু ঘটেছে, যার মধ্যে কিছু আমার নিজের জীবনের জন্য কালো ঘুঘু ছিল। কিন্তু এই অভিজ্ঞতা আমাকে বলেছে যে জীবন, ব্যবসায়ের মতোই, উত্থান-পতন, অজানা পূর্ণ। আমরা সবসময় আশা করি যে আমরা যা ঘটেছে তা থেকে কিছু শিখতে পারি এবং ধীরে ধীরে এমন সত্যের কাছে যেতে পারি যা সম্ভবত বিদ্যমান নেই।

  আমরা সবাই জানি যে একটি সক্রিয় শেয়ারের সাধারণত একটি ছোট প্রসার হয়, যখন এটি সক্রিয় হয় না। কেন এটি ঘটে? একটি সহজ এবং সুন্দর গাণিতিক মডেলের সাথে মূল্যের পার্থক্য ব্যাখ্যা করা যায়? আজ আমরা EKOP মডেল সম্পর্কে কথা বলব[[১] এই প্রবন্ধের শুরুতে, বিভিন্ন তথ্যের সাথে ব্যবসায়ীদের আচরণগুলি এই দুটি শ্রেণীর শেয়ারের দামের পার্থক্যের কারণ হতে পারে কিনা তা নিয়ে গবেষণা করা হয়েছিল। এই কলাম নিবন্ধে, আমি এই মডেলের ভিত্তি সম্পর্কে কথা বলব। মডেলের প্রয়োগগুলি পরবর্তী নিবন্ধে আরও বিশ্লেষণ করা হবে (যদি আমার সময় থাকে) । এই নিবন্ধে প্রদর্শিত গাণিতিক মডেলের সরলতার সৌন্দর্যটি নিখুঁত ছিল, নিবন্ধটি পড়ার প্রক্রিয়াটি উপভোগযোগ্য ছিল।

• ২ লেনদেনের প্রক্রিয়া অনুমান

  যখন আমরা একটি আর্থিক মডেল সম্পর্কে কথা বলি, তখন সবচেয়ে গুরুত্বপূর্ণ বিষয় হল এই মডেলের অনুমানগুলি। একটি ভাল আর্থিক মডেলের নিজস্ব অনুমান রয়েছেঃ এটি এত শক্তিশালী হবে না যে এটি সর্বজনীন হবে না; এটি এত দুর্বলও হবে না যে এটি সুন্দর এবং সংক্ষিপ্ত ফলাফলের দিকে পরিচালিত করবে না। EKOP মডেলের মূল অনুমানগুলি নিম্নরূপঃ

  অনুমান ১ঃ আমরা শেয়ারের লেনদেনের কথা বলছি, লেনদেনের ঘটনাটি দিনের মধ্যে বিচ্ছিন্ন, দিনের মধ্যে ধারাবাহিক অনুমান। অর্থাৎ, ব্যবসায়ীদের লেনদেন 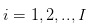এই বিচ্ছিন্ন লেনদেনের দিনগুলিতে ঘটেছিল। এবং লেনদেনের দিনে, লেনদেন 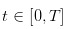এই ধারাবাহিক সময়ে ঘটেছিল।

  • খারাপ খবর হলো, আমরা স্টকটির মূল্য 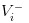হিসেবে লিখেছি।
  • ভালো খবর হলো, আমরা আমাদের শেয়ারের মূল্য /upload/asset/9efe14739d7dad9c5e883e2a0d6b38241a892641 লিখেছি।
  • কোন খবর না থাকায়, আমরা স্টক এর মূল্য

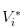
  স্পষ্টতই, আমাদের কাছে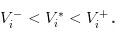

  অনুমান ২ঃ একটি নির্দিষ্ট দিনে,

  ০ এর সম্ভাব্যতা এমন একটি ঘটনা যা শেয়ারের দামকে প্রভাবিত করে, তবে ১-α এর সম্ভাবনা এমন একটি ঘটনা যা শেয়ারের দামকে প্রভাবিত করে না। যে দিনগুলিতে ঘটনাটি ঘটেছিল, সেখানে একটি খারাপ ঘটনা ঘটেছিল যা শেয়ারের দামকে কমিয়ে দেয় এবং একটি ভাল ঘটনা ঘটেছিল যা শেয়ারের দামকে বাড়িয়ে দেয়।

  অনুমান ৩ঃ শেয়ার ব্যবসায়ের অংশগ্রহণকারীরা বাজার প্রস্তুতকারক, অবগত ব্যবসায়ী, এবং অবগত ব্যবসায়ী। তারা যথাক্রমে নিম্নলিখিত ট্রেডিং আচরণ অনুসরণ করেঃ

  এমএম সর্বদা একটি ইউনিট কেনার বা বিক্রির জন্য প্রস্তুত থাকে এবং একজন বাজার ব্যবসায়ী হিসাবে তার দায়িত্ব পালন করে। এমএম ঝুঁকি-নিরপেক্ষ, তাই তার তালিকাভুক্ত মূল্যটি তার নিজের মতে ন্যায্য মূল্য।

  আইটি কেবলমাত্র সংবাদ প্রকাশের দিনই লেনদেন করে, তাদের লেনদেনের প্রক্রিয়াটি একটি বিরতিহীন প্রক্রিয়া। কোনও দিন, যদি খারাপ খবর আসে তবে তিনি একটি বিক্রয় লেনদেনের লেনদেনের লেনদেনের লেনদেনের লেনদেনের লেনদেনের লেনদেনের লেনদেনের লেনদেনের লেনদেনের লেনদেনের লেনদেনের লেনদেনের লেনদেনের লেনদেনের লেনদেনের লেনদেনের লেনদেনের লেনদেনের লেনদেনের লেনদেনের লেনদেনের লেনদেনের লেনদেনের লেনদেনের লেনদেনের লেনদেনের লেনদেনের লেনদেনের লেনদেনের লেনদেনের লেনদেনের লেনদেনের লেনদেনের লেনদেনের লেনদেনের লেনদেনের লেনদেনের লেনদেনের লেনদেনের লেনদেনের লেনদেনের লেনদেন

  ইউটি, আমাদের দরিদ্র সরিষা, তাদের লেনদেনের প্রক্রিয়াটিও একটি প্যাসিভ প্রক্রিয়া, কারণ তাদের কোনও বার্তা নেই, এবং প্রতিদিন, তারা লেনদেন এবং বিক্রয় লেনদেনের লেনদেনের লেনদেন করে।
  মনে রাখবেন, এখানে সকল বসন প্রক্রিয়া একে অপরের থেকে স্বতন্ত্র। আমরা একটি চিত্রের মাধ্যমে অনুমান 3 প্রদর্শন করতে পারি, যেমনঃ

  

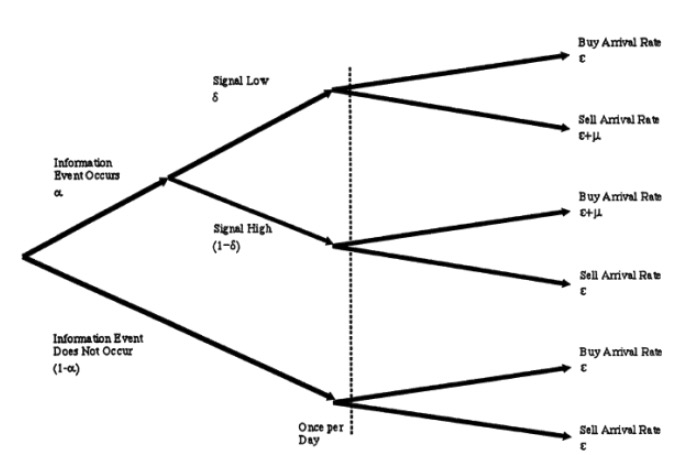
• ৩ লেনদেন এবং মূল্যের আপডেট

  আমরা জানি যে মার্কেটমার্কাররা সাধারণত বড় বড় কোম্পানিতে কাজ করে। তারা খুব বুদ্ধিমান, তারা দীর্ঘমেয়াদী আইটি এবং ইউটি-র সাথে লড়াই করার সময়, তারা প্রচুর historicalতিহাসিক ডেটা বিশ্লেষণের মাধ্যমে উপরের গাছের চিত্রের সমস্ত মডেল প্যারামিটারগুলি সংক্ষিপ্ত করে। তবে, ভাগ্যক্রমে, তারা জ্ঞানী ব্যবসায়ীদের মতো এতটা শক্তিশালী নয়, যখন কোনও ট্রেডিংয়ের দিনটি শুরু হতে চলেছে, তারা ব্যবসায়ীদের মতো জানেন না যে আজকের কোনও গুরুত্বপূর্ণ ঘটনা ঘটেছে কিনা।

  এখন, আসুন আমরা MM এর চরিত্রে অভিনয় করি, IT এবং UT এর সাথে লড়াই করি। একটি নির্দিষ্ট সময়ে t, আমরা নিজেদেরকে একটি ভেক্টর হিসেবে চিহ্নিত করি, যা কিছু না হওয়ার সম্ভাবনা, ভাল কিছু ঘটার সম্ভাবনা এবং খারাপ কিছু ঘটার সম্ভাবনা সম্পর্কে অনুমান করে।

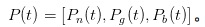  。 স্পষ্টতই, দিনের শুরুতে, যখন /upload/asset/7a5565722b92d2accf331f58923d6bab702659de.png, আমি একটি নোটও দেখিনি, তাই আমি যা বলতে পারি তা হল যে কিছুই ঘটার সম্ভাবনা α, ভাল কিছু ঘটার সম্ভাবনা /upload/asset/c9cf50c6146a25c662c593ed229845822bfac7a5.png, এবং খারাপ কিছু ঘটার সম্ভাবনা /upload/asset/87418f07b12b65fce4fc3f70b024e94d2e19f769a.png।

  কিভাবে এই সম্ভাব্যতা আপডেট করা যায়? ঠিক আছে, আমরা যারা বাজার নির্বাচন করি, আমরা সবাই Bayes's formula জানি। আমরা Bayes's law ব্যবহার করে আমাদের সম্ভাব্যতা অনুমান আপডেট করি যখন আমরা একটি বিক্রিত পয়েন্ট দেখতে পাই। আমরা প্রথমে আমাদের সম্ভাব্যতা অনুমান আপডেট করি, যা আজকের জন্য কোন খবর নেই।

  

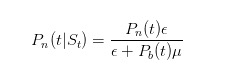
  এই সূত্রের মৌলিকটি হল যে, যখন কোন খবর নেই, তখন কেবল অজ্ঞ ব্যবসায়ীরাই বিড বিক্রি করবে; এবং বিভাজকটি হল যে, যে কোন সময় অজ্ঞ ব্যবসায়ীরা বিড বিক্রি করবে, এবং জ্ঞানী ব্যবসায়ীরা বিড বিক্রি করবে। একইভাবে, আমরা অনুমান করতে পারি

  

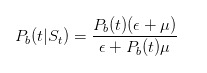
  এবং

  

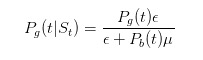
  কিন্তু আমরা এই ধারণার সাথে চলার আগে, আসুন আমরা কিছু সহজ পরীক্ষা করি। আমরা বলেছিলাম যে, যদি আমরা একটি বিক্রির বিজ্ঞপ্তি দেখি, তাহলে আমাদের অনুমান করা উচিত যে খারাপ কিছু ঘটার সম্ভাবনা অনেক বেশি। ঠিক আছে? আমরা একটি খুব সহজ ধারণার সাথে চলতে পারি।

  

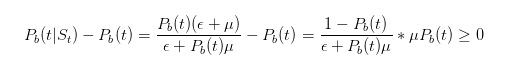
  এইভাবে, আমাদের অনুমানগুলি আমাদের অন্তর্দৃষ্টিকে সমর্থন করে।

  এখন, আপডেটেড সম্ভাব্যতা সহ, আমরা একটি যুক্তিসঙ্গত মূল্য গণনা করতে পারি, যা আমাদের বাজার থেকে কেনা মূল্য হিসাবে ব্যবহার করা হবে।

  

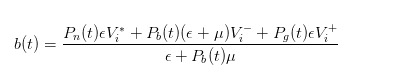
  আমরা দেখতে পাচ্ছি যে, যখন একটি ক্রয় আদেশ আসে, তখন আমরা বাজারদর হিসেবে যে মূল্য দিতে চাই তা হল

  

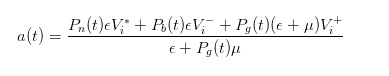
• 4 মূল্য পরিবর্তনের পরে মূল্যের পার্থক্যের প্রকাশ

  উপরের ক্রয় এবং বিক্রয় মূল্যের অভিব্যক্তিটি যথেষ্ট স্বজ্ঞাত নয়, আমরা এটিকে সরল করার জন্য স্টকটির প্রত্যাশিত মূল্যটি চালু করতে পারি। আমাদের প্রত্যাশিত মূল্যটি হল

  

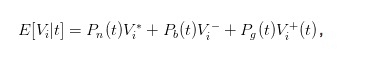
  সুতরাং, আমরা bid এবং ask এর এক্সপ্রেশনগুলোকে

  

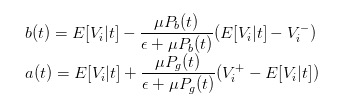
  সুতরাং, আমরা স্পষ্টভাবে বলতে পারি যে,

  

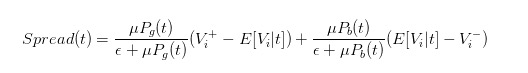
• ৫. ব্যবসায়ীদের আচরণে দামের পার্থক্যের প্রভাব

  এখন যেহেতু আমরা দামের বৈষম্য নিয়ে কথা বলছি, তাই আমরা বিভিন্ন ব্যবসায়ীদের দ্বারা দামের বৈষম্যের প্রভাব বিশ্লেষণ করতে পারি।

  লক্ষ্য করুন, ε হল অজ্ঞাত ব্যবসায়ীদের (আসুন আমরা তাদের 'ক্লিনার' বলি) প্রবেশাধিকার, এবং যদি ε >> μ হয়, আমরা দেখতে পারি, / upload/asset/539e0cfb1aae368277dd0e3840448b6a39abd087.png উভয়ই 0 এর দিকে এগিয়ে যাবে, যার অর্থ হল, স্প্রেডও 0 এর দিকে এগিয়ে যাবে।
  যদি আমরা অন্য প্রান্তে যাই, যদি আমরা ধরে নিই যে বাজারে আর কোন সরিষা নেই, কেবলমাত্র সরিষার চেয়ে আরও ভাল বুদ্ধিমান ব্যবসায়ীদের একটি গ্রুপ রয়েছে, তবে আমরা দুঃখজনকভাবে দেখতে পাব যে আমরা যে দামটি রেখেছি তা হ'ল 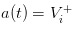এবং /upload/asset/1248ca7d3d472490982c9d0aa7b2e04b51269b18.png, তাই বুদ্ধিমান ব্যবসায়ীরা দেখতে পান যে তারা যেভাবে কিনবে বা বিক্রি করবে তা লাভজনক নয়, বাজারটি অবশ্যই নিস্তেজ হয়ে যাবে।

  দেখুন, আমরা কিছু অনুমানের উপর ভিত্তি করে, খুব সহজ গাণিতিক অনুমান ব্যবহার করে, এমন একটি মজার এবং গভীর সিদ্ধান্তে পৌঁছাতে সক্ষম হয়েছি, যা সম্ভবত গাণিতিক মডেলের দুর্দান্ত আকর্ষণ। এই নিবন্ধটি পড়ার পরে, আমি আশা করি আপনি রসুনের প্রতি সদয় হবেন, আমরা রসুনগুলিই বাজারটি সঠিকভাবে পরিচালনা করার গ্যারান্টি!

[1] Easley, David, et al. "Liquidity, information, and infrequently traded stocks." The Journal of Finance 51.4 (1996): 1405-1436.