উচ্চ-ফ্রিকোয়েন্সি ট্রেডিং কৌশল সম্পর্কে চিন্তাভাবনা (1)
 3
3
 4856
4856

নিবন্ধটি ডিজিটাল মুদ্রার জন্য উচ্চ-ফ্রিকোয়েন্সি ট্রেডিং কৌশল নিয়ে আলোচনা করে, যার মধ্যে রয়েছে লাভের উৎস (মূলত হিংসাত্মক বাজারের ওঠানামা এবং এক্সচেঞ্জ ফি রিবেট), অর্ডার প্লেসমেন্ট এবং পজিশন কন্ট্রোল এবং প্যারেটো ডিস্ট্রিবিউশন ব্যবহার করে ট্রেডিং ভলিউম মডেল করার পদ্ধতি। উপরন্তু, Binance দ্বারা প্রদত্ত ট্রেড-বাই-ট্রেড এবং সর্বোত্তম পেন্ডিং অর্ডার ডেটাও ব্যাকটেস্টিংয়ের জন্য উদ্ধৃত করা হয়েছিল, এবং পরবর্তী নিবন্ধগুলিতে গভীরভাবে উচ্চ-ফ্রিকোয়েন্সি ট্রেডিং কৌশলগুলির অন্যান্য বিষয়গুলি নিয়ে আলোচনা করার পরিকল্পনা করা হয়েছে।
আমি আগে ডিজিটাল মুদ্রার উচ্চ-ফ্রিকোয়েন্সি ট্রেডিং নিয়ে দুটি নিবন্ধ লিখেছি। ডিজিটাল মুদ্রার উচ্চ-ফ্রিকোয়েন্সি কৌশলগুলির একটি বিস্তারিত ভূমিকা, 5 দিনে 80 বার উপার্জন করুন, উচ্চ-ফ্রিকোয়েন্সি কৌশলের শক্তি. কিন্তু এটি শুধুমাত্র অভিজ্ঞতা ভাগ করে নেওয়া এবং সাধারণ শর্তে কথা বলা হিসাবে বিবেচিত হতে পারে। এইবার আমি শুরু থেকে উচ্চ-ফ্রিকোয়েন্সি ট্রেডিং এর ধারনাগুলিকে প্রবর্তন করার জন্য একটি সিরিজ লেখার পরিকল্পনা করছি গভীরভাবে নয় এই নিবন্ধটি শুধুমাত্র একটি ভূমিকা আমি আশা করি কেউ আমাকে সংশোধন করতে পারে.
উচ্চ ফ্রিকোয়েন্সি লাভ উত্স
পূর্ববর্তী নিবন্ধগুলিতে উল্লিখিত হিসাবে, উচ্চ-ফ্রিকোয়েন্সি কৌশলগুলি বিশেষভাবে সেই সমস্ত বাজারের জন্য উপযুক্ত যেখানে বাজার খুব তীব্রভাবে ওঠানামা করে৷ অল্প সময়ের মধ্যে একটি ট্রেডিং বৈচিত্র্যের মূল্য পরিবর্তনগুলি পরীক্ষা করুন, যা সাধারণ প্রবণতা এবং শক নিয়ে গঠিত। যদি আমরা সঠিকভাবে প্রবণতা পরিবর্তনের ভবিষ্যদ্বাণী করতে পারি, তাহলে অবশ্যই আমরা অর্থ উপার্জন করতে পারি, তবে এটি সবচেয়ে কঠিন এই নিবন্ধটি প্রধানত উচ্চ-ফ্রিকোয়েন্সি নির্মাতা কৌশলগুলি উপস্থাপন করে এবং এই সমস্যাটি কভার করবে না। একটি অস্থির বাজারে, যদি লেনদেনগুলি ঘন ঘন হয় এবং লাভের পরিমাণ যথেষ্ট হয়, তাহলে এইভাবে আপনি বাজারের পূর্বাভাস না দিয়েই লাভ করতে পারেন৷ বর্তমানে, এক্সচেঞ্জ মেকার লেনদেনে কমিশন রিবেট রয়েছে, যা লাভের একটি উপাদানও বটে, যত বেশি প্রতিযোগিতা থাকবে, ছাড়ের অনুপাত তত বেশি হবে।
সমস্যা সমাধান করা
কৌশলটি একই সময়ে ক্রয় এবং বিক্রয়ের আদেশ দেয় প্রথম প্রশ্নটি হল কোথায় অর্ডার দিতে হবে। দাম যত বেশি হ্যান্ডিক্যাপের কাছাকাছি, লেনদেনের সম্ভাবনা তত বেশি, তবে একটি অস্থির বাজারে, তাত্ক্ষণিক লেনদেনের মূল্য যদি খুব কাছাকাছি হয় তবে আপনি করতে পারবেন না যথেষ্ট লাভ। যে অর্ডারগুলি খুব দূরে রাখা হয় সেগুলির বন্ধ হওয়ার সম্ভাবনা কম। এটি একটি সমস্যা যা অপ্টিমাইজেশান প্রয়োজন।
কন্ট্রোল পজিশন। ঝুঁকি নিয়ন্ত্রণ করার জন্য, কৌশলটি দীর্ঘ সময়ের জন্য খুব বেশি অবস্থান জমা করতে পারে না। এটি মুলতুবি আদেশের দূরত্ব, মুলতুবি আদেশের পরিমাণ এবং মোট অবস্থানের সীমা নিয়ন্ত্রণ করে সমাধান করা যেতে পারে।
উপরোক্ত লক্ষ্যগুলি অর্জনের জন্য, লেনদেনের সম্ভাবনা, লেনদেনের মুনাফা, বাজার অনুমান এবং অন্যান্য দিকগুলির মডেল এবং অনুমান করা প্রয়োজন। এই ক্ষেত্রে অনেক নিবন্ধ এবং গবেষণাপত্র রয়েছে, যা উচ্চ-ফ্রিকোয়েন্সি ট্রেডিং এর মতো কীওয়ার্ড সহ পাওয়া যেতে পারে। , অর্ডারবুক, ইত্যাদি। অনলাইনে অনেক সুপারিশ আছে, যেগুলো আমি এখানে আলোচনা করব না। উপরন্তু, একটি নির্ভরযোগ্য এবং দ্রুত ব্যাকটেস্টিং সিস্টেম স্থাপন করা সর্বোত্তম। যদিও উচ্চ-ফ্রিকোয়েন্সি কৌশলগুলি তাদের কার্যকারিতা যাচাই করার জন্য বাস্তব ট্রেডিংয়ের মাধ্যমে সহজেই যাচাই করা যেতে পারে, ব্যাকটেস্টিং এখনও আরও ধারণা প্রদান করতে পারে এবং ট্রায়াল এবং ত্রুটির খরচ কমাতে পারে।
প্রয়োজনীয় তথ্য
Binance লেনদেন দ্বারা লেনদেন এবং সর্বোত্তম মুলতুবি অর্ডার ডেটা প্রদান করে।ডাউনলোড, হোয়াইটলিস্টে API ব্যবহার করে গভীরতার ডেটা ডাউনলোড করতে হবে, অথবা আপনি নিজে সংগ্রহ করতে পারেন। ব্যাকটেস্টিং উদ্দেশ্যে, শুধুমাত্র সংগৃহীত লেনদেন ডেটা ব্যবহার করুন। এই নিবন্ধটি একটি উদাহরণ হিসাবে HOOKUSDT-aggTrades-2023-01-27-এর ডেটা নেয়৷
from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
লেনদেন দ্বারা লেনদেন কলাম নিম্নরূপ:
- agg_trade_id: সমষ্টিগত লেনদেন নথির আইডি,
- মূল্য: লেনদেনের মূল্য
- পরিমাণ: লেনদেনের পরিমাণ
- first_trade_id: সংগ্রহে একই সময়ে একাধিক লেনদেন হতে পারে, শুধুমাত্র একটি ডেটা গণনা করা হয়, এটি প্রথম লেনদেনের আইডি।
- last_trade_id: শেষ লেনদেনের আইডি
- লেনদেন_সময়: লেনদেনের সময়
- is_buyer_maker: লেনদেনের দিকনির্দেশ, সত্য মানে হল ক্রয় অর্ডার প্রস্তুতকারী দ্বারা করা হয়, এবং বিক্রয় আদেশ গ্রহণকারী দ্বারা নেওয়া হয়।
আপনি দেখতে পারেন যে সেদিন 660,000 লেনদেন ডেটা ছিল এবং লেনদেনগুলি খুব সক্রিয় ছিল৷ csv মন্তব্য এলাকায় সংযুক্ত করা হবে.
trades = pd.read_csv('COMPUSDT-aggTrades-2023-07-02.csv')
trades
664475 rows × 7 columns
| agg_trade_id | price | quantity | first_trade_id | last_trade_id | transact_time | is_buyer_maker |
|---|---|---|---|---|---|---|
| 120719552 | 52.42 | 22.087 | 207862988 | 207862990 | 1688256004603 | False |
| 120719553 | 52.41 | 29.314 | 207862991 | 207863002 | 1688256004623 | True |
| 120719554 | 52.42 | 0.945 | 207863003 | 207863003 | 1688256004678 | False |
| 120719555 | 52.41 | 13.534 | 207863004 | 207863006 | 1688256004680 | True |
| … | … | … | … | … | … | … |
| 121384024 | 68.29 | 10.065 | 210364899 | 210364905 | 1688342399863 | False |
| 121384025 | 68.30 | 7.078 | 210364906 | 210364908 | 1688342399948 | False |
| 121384026 | 68.29 | 7.622 | 210364909 | 210364911 | 1688342399979 | True |
একক লেনদেন ভলিউম মডেলিং
প্রথমত, ডেটা প্রক্রিয়া করা হয় এবং আসল ট্রেডগুলিকে সক্রিয় ক্রয় অর্ডার গ্রুপে ভাগ করা হয় এবং অর্ডার সক্রিয় ডিল গ্রুপে বিক্রি করা হয়। উপরন্তু, মূল মোট লেনদেনের ডেটা হল একই মূল্য এবং একই সময়ে একই দিকনির্দেশ সহ একটি সক্রিয় ক্রয় অর্ডার হতে পারে 100 এর পরিমাণে। যদি এটি একাধিক লেনদেনে বিভক্ত হয় এবং মূল্যগুলি হয়। ভিন্ন, উদাহরণস্বরূপ, এটি দুটি লেনদেনে বিভক্ত: 60 এবং 40। দুটি টুকরো ডেটা তৈরি হবে, যা ক্রয়ের অর্ডারের পরিমাণের অনুমানকে প্রভাবিত করবে। অতএব, লেনদেন_সময়ের উপর ভিত্তি করে আবার একত্রিত করা প্রয়োজন। একত্রিত করার পরে, ডেটার পরিমাণ 140,000 আইটেম দ্বারা হ্রাস করা হয়েছিল।
trades['date'] = pd.to_datetime(trades['transact_time'], unit='ms')
trades.index = trades['date']
buy_trades = trades[trades['is_buyer_maker']==False].copy()
sell_trades = trades[trades['is_buyer_maker']==True].copy()
buy_trades = buy_trades.groupby('transact_time').agg({
'agg_trade_id': 'last',
'price': 'last',
'quantity': 'sum',
'first_trade_id': 'first',
'last_trade_id': 'last',
'is_buyer_maker': 'last',
'date': 'last',
'transact_time':'last'
})
sell_trades = sell_trades.groupby('transact_time').agg({
'agg_trade_id': 'last',
'price': 'last',
'quantity': 'sum',
'first_trade_id': 'first',
'last_trade_id': 'last',
'is_buyer_maker': 'last',
'date': 'last',
'transact_time':'last'
})
buy_trades['interval']=buy_trades['transact_time'] - buy_trades['transact_time'].shift()
sell_trades['interval']=sell_trades['transact_time'] - sell_trades['transact_time'].shift()
print(trades.shape[0] - (buy_trades.shape[0]+sell_trades.shape[0]))
146181
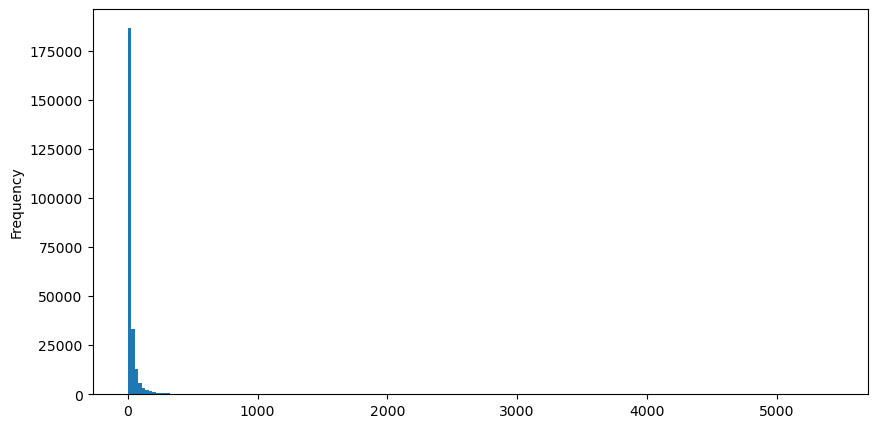
উদাহরণ হিসেবে ক্রয়ের অর্ডার নিয়ে, প্রথমে একটি হিস্টোগ্রাম আঁকুন। আপনি দেখতে পাচ্ছেন যে লং-টেইল প্রভাবটি খুবই স্পষ্ট। বেশিরভাগ ডেটা খুব বাম দিকে কেন্দ্রীভূত, তবে টেইলে অল্প সংখ্যক বড় লেনদেনও বিতরণ করা হয়। .
buy_trades['quantity'].plot.hist(bins=200,figsize=(10, 5));
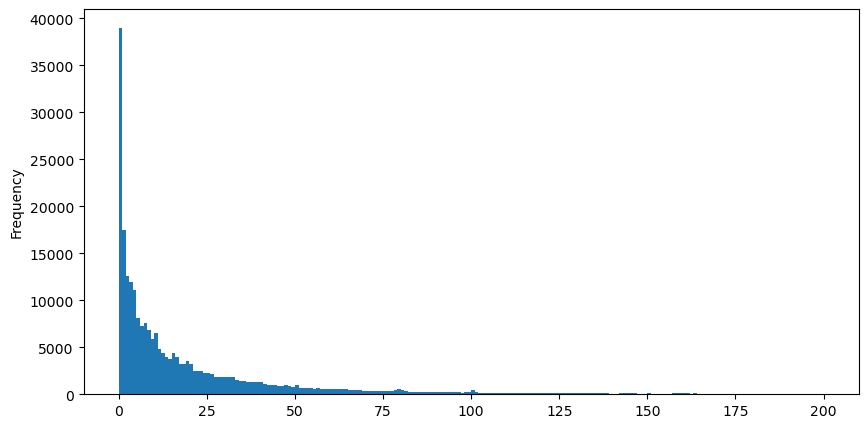
পর্যবেক্ষণের সুবিধার জন্য, পর্যবেক্ষণের জন্য লেজটি কেটে দেওয়া হয়, এটি দেখা যায় যে ট্রেডিং ভলিউম যত বেশি হবে, সংঘটনের ফ্রিকোয়েন্সি তত কম হবে এবং দ্রুত হ্রাস পাবে।
buy_trades['quantity'][buy_trades['quantity']<200].plot.hist(bins=200,figsize=(10, 5));
ট্রেডিং ভলিউম সন্তুষ্টি বন্টন সম্পর্কিত অনেক গবেষণা আছে. এটি পাওয়ার-আইন বন্টনকে সন্তুষ্ট করে, যাকে প্যারেটো ডিস্ট্রিবিউশনও বলা হয়, যা পরিসংখ্যানগত পদার্থবিদ্যা এবং সামাজিক বিজ্ঞানে একটি সাধারণ সম্ভাব্যতা বন্টন ফর্ম। পাওয়ার-ল ডিস্ট্রিবিউশনে, ইভেন্টের আকারের (বা ফ্রিকোয়েন্সি) সম্ভাবনা সেই ইভেন্টের আকারের কিছু নেতিবাচক সূচকের সমানুপাতিক। বিতরণের এই ফর্মের প্রধান বৈশিষ্ট্য হল যে বড় ঘটনাগুলি (অর্থাৎ যেগুলি গড় থেকে দূরে) অন্যান্য অনেকগুলি বিতরণে প্রত্যাশিত হওয়ার চেয়ে বেশি ঘন ঘন ঘটে। এটি ঠিক ভলিউম বিতরণের বৈশিষ্ট্য। Pareto বিতরণের ফর্ম হল: P(x) = Cx^(-α)। এটি নীচে প্রমাণিত হবে।
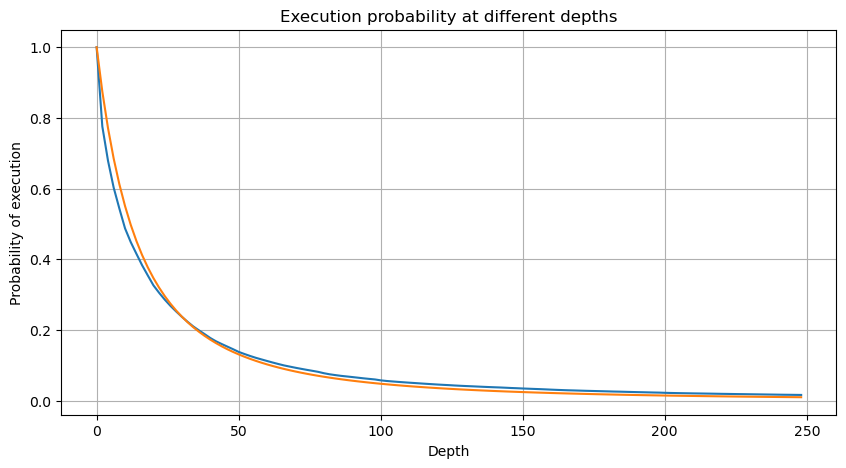
নিচের চিত্রটি একটি নির্দিষ্ট মানের চেয়ে ট্রেডিং ভলিউম বেশি হওয়ার সম্ভাবনা দেখায়। নীল রেখা হল প্রকৃত সম্ভাব্যতা, এবং কমলা রেখা হল সিমুলেটেড সম্ভাব্যতা। এখানে নির্দিষ্ট পরামিতিগুলি নিয়ে চিন্তা করবেন না। আপনি দেখতে পাচ্ছেন যে এটি করে পেরেটো বিতরণ পূরণ করুন। যেহেতু অর্ডারের পরিমাণ 0 এর চেয়ে বেশি হওয়ার সম্ভাবনা 1, এবং মানীকরণের প্রয়োজনীয়তা পূরণের জন্য, বন্টন সমীকরণটি নিম্নরূপ হওয়া উচিত:
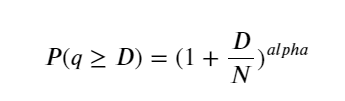
যেখানে N হল প্রমিত প্যারামিটার। এখানে, গড় ট্রেডিং ভলিউম M নির্বাচন করা হয়েছে, এবং আলফা নির্বাচন করা হয়েছে -2.06। নির্দিষ্ট আলফার অনুমান P মান দ্বারা ফিরে গণনা করা যেতে পারে যখন D=N। বিশেষভাবে: alpha = log(P(d>M))/log(2)। আলফা মান নির্বাচিত বিন্দুর উপর নির্ভর করে সামান্য ভিন্ন হবে।
depths = range(0, 250, 2)
probabilities = np.array([np.mean(buy_trades['quantity'] > depth) for depth in depths])
alpha = np.log(np.mean(buy_trades['quantity'] > mean_quantity))/np.log(2)
mean_quantity = buy_trades['quantity'].mean()
probabilities_s = np.array([(1+depth/mean_quantity)**alpha for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities)
plt.plot(depths, probabilities_s)
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.grid(True)
plt.figure(figsize=(10, 5))
plt.grid(True)
plt.title('Diff')
plt.plot(depths, probabilities_s-probabilities);
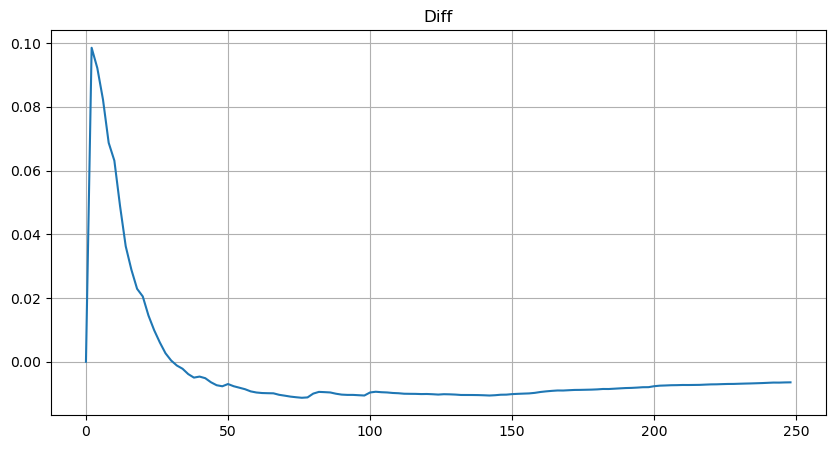
কিন্তু এই অনুমানটি শুধুমাত্র এটির মতই দেখায়। যখন ট্রেডিং ভলিউম ছোট হয়, তখন বিচ্যুতি বড় হয়, এমনকি 10% এর কাছাকাছি। আপনি প্যারামিটার অনুমানের সময় বিভিন্ন বিন্দু নির্বাচন করে এই বিন্দুর সম্ভাব্যতাকে আরও নির্ভুল করে তুলতে পারেন, কিন্তু এটি বিচ্যুতির সমস্যার সমাধান করে না। এটি ক্ষমতা আইন বন্টন এবং প্রকৃত বন্টন মধ্যে পার্থক্য দ্বারা নির্ধারিত হয় আরো সঠিক ফলাফল পেতে, ক্ষমতা আইন বন্টন এর সমীকরণ সংশোধন করা প্রয়োজন. আমি নির্দিষ্ট প্রক্রিয়া সম্পর্কে বিশদে যাব না, একটি অনুপ্রেরণা ঘটেছে এবং আমি খুঁজে পেয়েছি যে প্রকৃত প্রক্রিয়াটি নিম্নরূপ হওয়া উচিত:
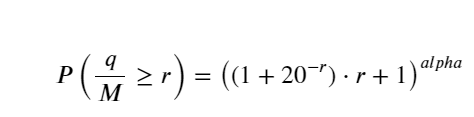
পরিচিতির সুবিধার্থে, r = q/M এখানে ব্যবহার করা হয়েছে স্বাভাবিক ট্রেডিং ভলিউম উপস্থাপন করতে। পরামিতি উপরের হিসাবে একই ভাবে অনুমান করা যেতে পারে. নীচের ছবিটি থেকে, আপনি দেখতে পাচ্ছেন যে সংশোধনের পরে সর্বাধিক বিচ্যুতি 2% এর বেশি হবে না, তাত্ত্বিকভাবে সংশোধন করা যেতে পারে, তবে এই নির্ভুলতা যথেষ্ট।
depths = range(0, 250, 2)
probabilities = np.array([np.mean(buy_trades['quantity'] > depth) for depth in depths])
mean = buy_trades['quantity'].mean()
alpha = np.log(np.mean(buy_trades['quantity'] > mean))/np.log(2.05)
probabilities_s = np.array([(((1+20**(-depth/mean))*depth+mean)/mean)**alpha for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities)
plt.plot(depths, probabilities_s)
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.grid(True)
plt.figure(figsize=(10, 5))
plt.grid(True)
plt.title('Diff')
plt.plot(depths, probabilities_s-probabilities);
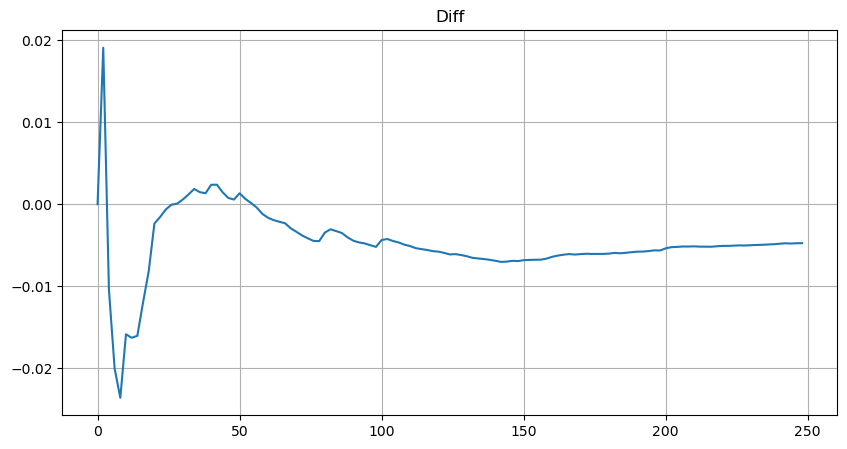
ট্রেডিং ভলিউম ডিস্ট্রিবিউশনের অনুমান সমীকরণের সাথে, দয়া করে মনে রাখবেন যে সমীকরণের সম্ভাব্যতা একটি বাস্তব সম্ভাবনা নয়, তবে একটি শর্তসাপেক্ষ সম্ভাবনা। এই মুহুর্তে আমরা এই প্রশ্নের উত্তর দিতে পারি, যদি পরবর্তী আদেশটি ঘটে তবে এই আদেশটি একটি নির্দিষ্ট মানের চেয়ে বেশি হওয়ার সম্ভাবনা কত? এটিও বলা যেতে পারে যে বিভিন্ন গভীরতার আদেশগুলি সম্পন্ন হওয়ার সম্ভাবনা কত (আদর্শভাবে, এটি এতটা কঠোর নয়। তত্ত্বগতভাবে, অর্ডার বইটিতে নতুন অর্ডার এবং বাতিল করা আদেশ রয়েছে, পাশাপাশি একই গভীরতায় সারি রয়েছে)।
এখানে লেখার দৈর্ঘ্য প্রায় একই, এবং এখনও অনেক প্রশ্ন আছে যার উত্তর দিতে হবে নিচের প্রবন্ধে।