উচ্চ-ফ্রিকোয়েন্সি ট্রেডিং কৌশল সম্পর্কে চিন্তাভাবনা (2)
 1
1
 3416
3416
নিবন্ধটি প্রধানত উচ্চ-ফ্রিকোয়েন্সি ট্রেডিং কৌশল নিয়ে আলোচনা করে, ক্রমবর্ধমান ভলিউম মডেলিং এবং মূল্যের প্রভাবের উপর ফোকাস করে। নিবন্ধটি একক লেনদেনের প্রভাব, স্থির-ব্যবধানের মূল্য শক, এবং দামের উপর লেনদেনের পরিমাণ বিশ্লেষণ করে একটি প্রাথমিক সর্বোত্তম মুলতুবি অর্ডার অবস্থান মডেলের প্রস্তাব করে। এই মডেল ভলিউম এবং মূল্য শক বোঝার উপর ভিত্তি করে সর্বোত্তম ট্রেডিং অবস্থান খুঁজে বের করার চেষ্টা করে। মডেলের অনুমানগুলি গভীরভাবে আলোচনা করা হয়েছিল, এবং মডেলের দ্বারা পূর্বাভাসিতদের সাথে প্রকৃত প্রত্যাশিত আয়ের তুলনা করে সর্বোত্তম মুলতুবি অর্ডার অবস্থানের একটি প্রাথমিক মূল্যায়ন করা হয়েছিল।
ক্রমবর্ধমান ভলিউম মডেলিং
পূর্ববর্তী নিবন্ধে একটি নির্দিষ্ট মানের চেয়ে বেশি লেনদেনের পরিমাণের সম্ভাব্যতা প্রকাশ করা হয়েছিল:
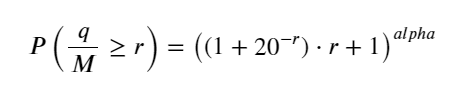
আমরা নির্দিষ্ট সময়ের মধ্যে ট্রেডিং ভলিউমের বন্টন নিয়েও উদ্বিগ্ন, যা প্রতিটি ট্রেডিং ভলিউম এবং অর্ডার ফ্রিকোয়েন্সির সাথে স্বজ্ঞাতভাবে সম্পর্কিত হওয়া উচিত। এর পরে, ডেটা নির্দিষ্ট ব্যবধানে প্রক্রিয়া করা হয়। উপরের হিসাবে এর বিতরণ আঁকুন।
from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
trades = pd.read_csv('HOOKUSDT-aggTrades-2023-01-27.csv')
trades['date'] = pd.to_datetime(trades['transact_time'], unit='ms')
trades.index = trades['date']
buy_trades = trades[trades['is_buyer_maker']==False].copy()
buy_trades = buy_trades.groupby('transact_time').agg({
'agg_trade_id': 'last',
'price': 'last',
'quantity': 'sum',
'first_trade_id': 'first',
'last_trade_id': 'last',
'is_buyer_maker': 'last',
'date': 'last',
'transact_time':'last'
})
buy_trades['interval']=buy_trades['transact_time'] - buy_trades['transact_time'].shift()
buy_trades.index = buy_trades['date']
প্রতিটি লেনদেনের জন্য প্রতি 1 সেকেন্ডে লেনদেন ভলিউম একত্রিত করুন, যে অংশটি ঘটেনি তা সরিয়ে ফেলুন এবং এটিকে মানানসই করতে উপরের একক লেনদেনটি ব্যবহার করুন যে ফলাফলটি 1 সেকেন্ডের মধ্যে ভাল একক লেনদেন, এবং সমস্যা একটি সমাধান সমস্যা হয়ে ওঠে. কিন্তু যখন সময়কাল বৃদ্ধি পায় (লেনদেনের ফ্রিকোয়েন্সি আপেক্ষিক), এটি পাওয়া যায় যে ত্রুটি বৃদ্ধি পায়, এবং গবেষণায় দেখা গেছে যে এই ত্রুটিটি পূর্ববর্তী প্যারেটো বিতরণ সংশোধন শব্দ দ্বারা সৃষ্ট। এটি দেখায় যে যখন সময়কাল দীর্ঘায়িত হয়, তত বেশি একক লেনদেন অন্তর্ভুক্ত করা হয়, একাধিক লেনদেনের সংমিশ্রণটি প্যারেটো বিতরণের কাছাকাছি হয় এই ক্ষেত্রে, সংশোধন শব্দটি সরানো প্রয়োজন৷
df_resampled = buy_trades['quantity'].resample('1S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]
buy_trades
| agg_trade_id | price | quantity | first_trade_id | last_trade_id | is_buyer_maker | date | transact_time | interval | diff | |
|---|---|---|---|---|---|---|---|---|---|---|
| 2023-01-27 00:00:00.161 | 1138369 | 2.901 | 54.3 | 3806199 | 3806201 | False | 2023-01-27 00:00:00.161 | 1674777600161 | NaN | 0.001 |
| 2023-01-27 00:00:04.140 | 1138370 | 2.901 | 291.3 | 3806202 | 3806203 | False | 2023-01-27 00:00:04.140 | 1674777604140 | 3979.0 | 0.000 |
| 2023-01-27 00:00:04.339 | 1138373 | 2.902 | 55.1 | 3806205 | 3806207 | False | 2023-01-27 00:00:04.339 | 1674777604339 | 199.0 | 0.001 |
| 2023-01-27 00:00:04.772 | 1138374 | 2.902 | 1032.7 | 3806208 | 3806223 | False | 2023-01-27 00:00:04.772 | 1674777604772 | 433.0 | 0.000 |
| 2023-01-27 00:00:05.562 | 1138375 | 2.901 | 3.5 | 3806224 | 3806224 | False | 2023-01-27 00:00:05.562 | 1674777605562 | 790.0 | 0.000 |
| … | … | … | … | … | … | … | … | … | … | … |
| 2023-01-27 23:59:57.739 | 1544370 | 3.572 | 394.8 | 5074645 | 5074651 | False | 2023-01-27 23:59:57.739 | 1674863997739 | 1224.0 | 0.002 |
| 2023-01-27 23:59:57.902 | 1544372 | 3.573 | 177.6 | 5074652 | 5074655 | False | 2023-01-27 23:59:57.902 | 1674863997902 | 163.0 | 0.001 |
| 2023-01-27 23:59:58.107 | 1544373 | 3.573 | 139.8 | 5074656 | 5074656 | False | 2023-01-27 23:59:58.107 | 1674863998107 | 205.0 | 0.000 |
| 2023-01-27 23:59:58.302 | 1544374 | 3.573 | 60.5 | 5074657 | 5074657 | False | 2023-01-27 23:59:58.302 | 1674863998302 | 195.0 | 0.000 |
| 2023-01-27 23:59:59.894 | 1544376 | 3.571 | 12.1 | 5074662 | 5074664 | False | 2023-01-27 23:59:59.894 | 1674863999894 | 1592.0 | 0.000 |
#1s内的累计分布
depths = np.array(range(0, 3000, 5))
probabilities = np.array([np.mean(df_resampled['quantity'] > depth) for depth in depths])
mean = df_resampled['quantity'].mean()
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2.05)
probabilities_s = np.array([((1+20**(-depth/mean))*depth/mean+1)**(alpha) for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities)
plt.plot(depths, probabilities_s)
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.grid(True)
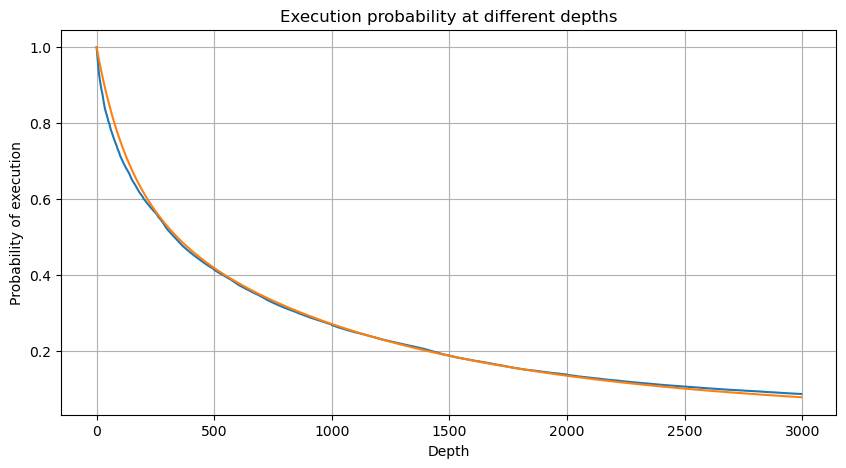
df_resampled = buy_trades['quantity'].resample('30S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]
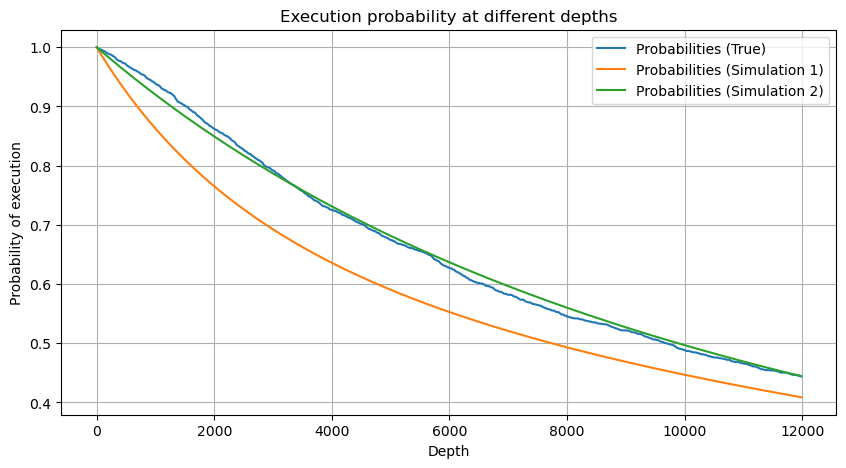
depths = np.array(range(0, 12000, 20))
probabilities = np.array([np.mean(df_resampled['quantity'] > depth) for depth in depths])
mean = df_resampled['quantity'].mean()
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2.05)
probabilities_s = np.array([((1+20**(-depth/mean))*depth/mean+1)**(alpha) for depth in depths])
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2)
probabilities_s_2 = np.array([(depth/mean+1)**alpha for depth in depths]) # 无修正
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities,label='Probabilities (True)')
plt.plot(depths, probabilities_s, label='Probabilities (Simulation 1)')
plt.plot(depths, probabilities_s_2, label='Probabilities (Simulation 2)')
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.legend()
plt.grid(True)
এখন আমরা বিভিন্ন সময়ে সঞ্চিত ট্রেডিং ভলিউমের বণ্টনের জন্য একটি সাধারণ সূত্র সংক্ষিপ্ত করতে পারি এবং প্রতিবার আলাদাভাবে গণনা করার পরিবর্তে একটি একক লেনদেনের বন্টন ব্যবহার করতে পারি। প্রক্রিয়াটি এখানে বাদ দেওয়া হয়েছে এবং সূত্রটি সরাসরি দেওয়া হয়েছে:
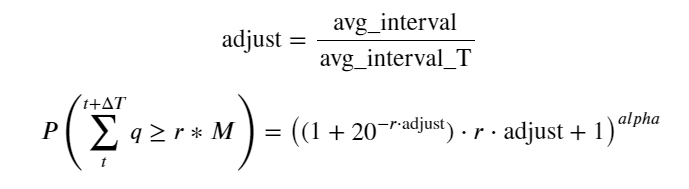
তাদের মধ্যে, avg_interval একটি একক লেনদেনের গড় ব্যবধানকে প্রতিনিধিত্ব করে এবং avg_interval_T অনুমান করা প্রয়োজন এমন বিরতির গড় ব্যবধানকে প্রতিনিধিত্ব করে, যা কিছুটা বিভ্রান্তিকর। যদি আমরা 1 সেকেন্ডের মধ্যে লেনদেন অনুমান করতে চাই, তাহলে আমাদের 1 সেকেন্ডের মধ্যে লেনদেন অন্তর্ভুক্ত ইভেন্টগুলির গড় ব্যবধান গণনা করতে হবে। যদি অর্ডার আগমনের সম্ভাব্যতা পয়সন বিতরণের সাথে সামঞ্জস্যপূর্ণ হয় তবে এটি এখানে সরাসরি অনুমান করা উচিত, তবে প্রকৃত বিচ্যুতিটি খুব বড় এবং এখানে ব্যাখ্যা করা হবে না।
মনে রাখবেন যে একটি নির্দিষ্ট ব্যবধানের মধ্যে একটি নির্দিষ্ট মানের চেয়ে ভলিউম বেশি হওয়ার সম্ভাবনা গভীরতার সেই অবস্থানে লেনদেনের প্রকৃত সম্ভাবনা থেকে বেশ আলাদা হওয়া উচিত, কারণ অপেক্ষার সময় যত বেশি হবে, অর্ডার বইয়ের সম্ভাবনা তত বেশি হবে। পরিবর্তন হয়, এবং লেনদেনের ফলে গভীরতাও পরিবর্তিত হয়, তাই ডেটা আপডেট হওয়ার সাথে সাথে একই গভীরতার অবস্থানে লেনদেনের সম্ভাবনা বাস্তব সময়ে পরিবর্তিত হয়।
df_resampled = buy_trades['quantity'].resample('2S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]
depths = np.array(range(0, 6500, 10))
probabilities = np.array([np.mean(df_resampled['quantity'] > depth) for depth in depths])
mean = buy_trades['quantity'].mean()
adjust = buy_trades['interval'].mean() / 2620
alpha = np.log(np.mean(buy_trades['quantity'] > mean))/0.7178397931503168
probabilities_s = np.array([((1+20**(-depth*adjust/mean))*depth*adjust/mean+1)**(alpha) for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities)
plt.plot(depths, probabilities_s)
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.grid(True)
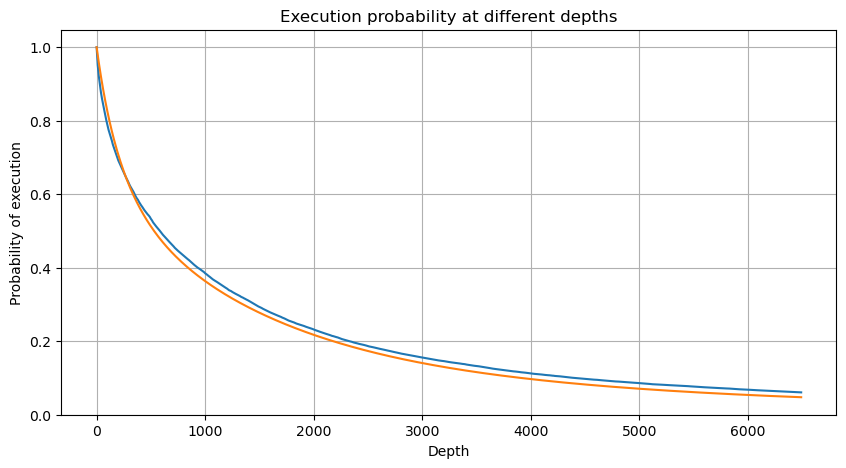
একক লেনদেন মূল্য প্রভাব
লেনদেন ডেটা একটি ধন, এবং এখনও প্রচুর ডেটা রয়েছে যা খনন করা যেতে পারে। মূল্যের উপর অর্ডারের প্রভাব সম্পর্কে আমাদের খুব উদ্বিগ্ন হওয়া উচিত, যা কৌশলটির মুলতুবি অর্ডার অবস্থানকে প্রভাবিত করে। একইভাবে, ট্রানজ্যাক্ট_টাইমের উপর ভিত্তি করে ডেটা একত্রিত করা হয় এবং শেষ মূল্য এবং প্রথম মূল্যের মধ্যে পার্থক্য গণনা করা হয় যদি শুধুমাত্র একটি অর্ডার থাকে তবে পার্থক্যটি 0। আশ্চর্যের বিষয় হল যে এখনও অল্প সংখ্যক ডেটা ফলাফল রয়েছে যা ডেটা বিন্যাসের ক্রম নিয়ে সমস্যা হওয়া উচিত এবং আমি এখানে এটিতে যাব না।
ফলাফলগুলি দেখায় যে নো ইমপ্যাক্ট অনুপাত 77%, 1 টিকের অনুপাত 16.5%, 2 টিকের অনুপাত 3.7%, 3 টি টিকগুলির অনুপাত 1.2% এবং 4টির বেশি অনুপাত টিক 1% এর কম। এটি মূলত সূচকীয় ফাংশনের বৈশিষ্ট্যগুলির সাথে সামঞ্জস্যপূর্ণ, তবে ফিটিংটি সঠিক নয়।
লেনদেনের পরিমাণ যা সংশ্লিষ্ট মূল্যের পার্থক্যের কারণ হয়েছিল তা গণনা করা হয়েছিল, এবং খুব বেশি প্রভাবের কারণে সৃষ্ট বিকৃতি অপসারণ করা হয়েছিল। এটি মূলত রৈখিক সম্পর্কের সাথে সঙ্গতিপূর্ণ, এবং প্রায় প্রতি 1,000 ভলিউমে 1 টি টিক মূল্যের ওঠানামা ঘটে। এটাও বোঝা যায় যে প্রতিটি মূল্যের কাছাকাছি পেন্ডিং অর্ডারের গড় সংখ্যা প্রায় ১,০০০।
diff_df = trades[trades['is_buyer_maker']==False].groupby('transact_time')['price'].agg(lambda x: abs(round(x.iloc[-1] - x.iloc[0],3)) if len(x) > 1 else 0)
buy_trades['diff'] = buy_trades['transact_time'].map(diff_df)
diff_counts = buy_trades['diff'].value_counts()
diff_counts[diff_counts>10]/diff_counts.sum()
0.000 0.769965
0.001 0.165527
0.002 0.037826
0.003 0.012546
0.004 0.005986
0.005 0.003173
0.006 0.001964
0.007 0.001036
0.008 0.000795
0.009 0.000474
0.010 0.000227
0.011 0.000187
0.012 0.000087
0.013 0.000080
Name: diff, dtype: float64
diff_group = buy_trades.groupby('diff').agg({
'quantity': 'mean',
'diff': 'last',
})
diff_group['quantity'][diff_group['diff']>0][diff_group['diff']<0.01].plot(figsize=(10,5),grid=True);
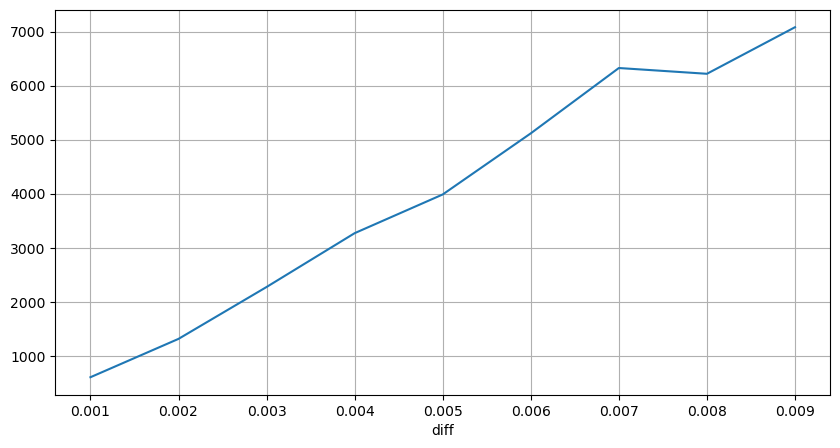
নির্দিষ্ট-ব্যবধান মূল্য শক
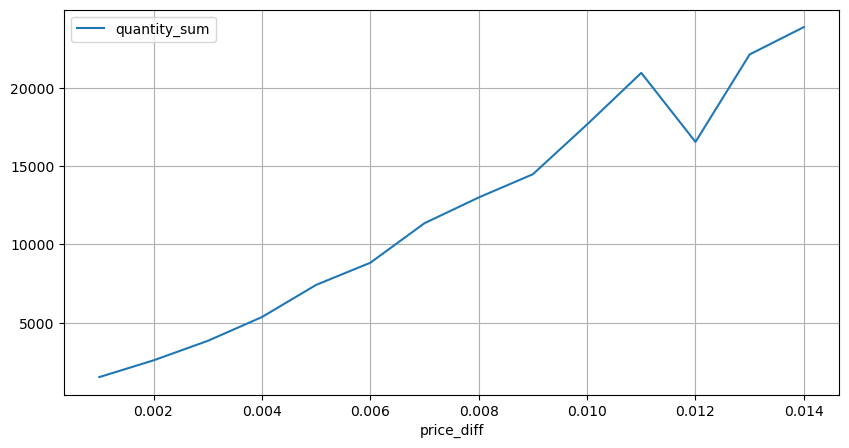
2 সেকেন্ডের মধ্যে মূল্যের প্রভাব গণনা করা হয় যে এখানে একটি নেতিবাচক মান থাকবে, যেহেতু এখানে শুধুমাত্র ক্রয় অর্ডারগুলি গণনা করা হয়, তাই প্রতিসম অবস্থানটি একটি টিক বড় হবে৷ ট্রেডিং ভলিউম এবং প্রভাবের মধ্যে সম্পর্ক পর্যবেক্ষণ করা চালিয়ে যান, এবং শুধুমাত্র 0-এর বেশি ফলাফল গণনা করুন। উপসংহারটি একটি একক অর্ডারের মতো, এবং এটি একটি আনুমানিক রৈখিক সম্পর্কও প্রতিটি টিকের জন্য প্রায় 2,000 ভলিউম প্রয়োজন।
df_resampled = buy_trades.resample('2S').agg({
'price': ['first', 'last', 'count'],
'quantity': 'sum'
})
df_resampled['price_diff'] = round(df_resampled[('price', 'last')] - df_resampled[('price', 'first')],3)
df_resampled['price_diff'] = df_resampled['price_diff'].fillna(0)
result_df_raw = pd.DataFrame({
'price_diff': df_resampled['price_diff'],
'quantity_sum': df_resampled[('quantity', 'sum')],
'data_count': df_resampled[('price', 'count')]
})
result_df = result_df_raw[result_df_raw['price_diff'] != 0]
result_df['price_diff'][abs(result_df['price_diff'])<0.016].value_counts().sort_index().plot.bar(figsize=(10,5));
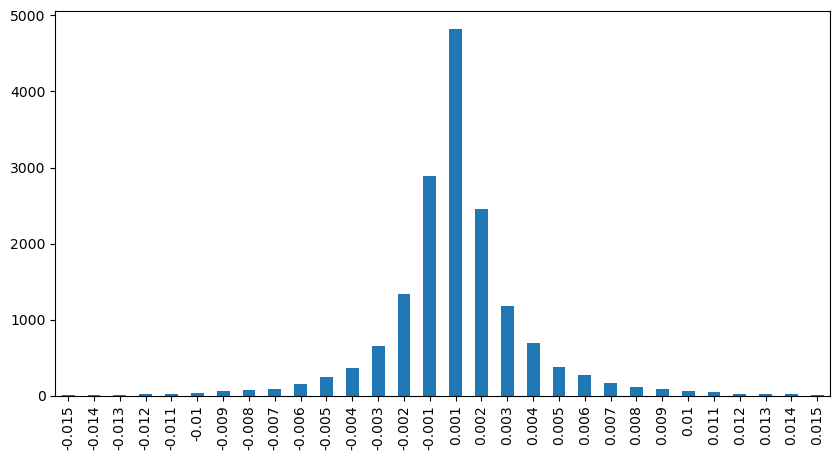
result_df['price_diff'].value_counts()[result_df['price_diff'].value_counts()>30]
0.001 7176
-0.001 3665
0.002 3069
-0.002 1536
0.003 1260
0.004 692
-0.003 608
0.005 391
-0.004 322
0.006 259
-0.005 192
0.007 146
-0.006 112
0.008 82
0.009 75
-0.007 75
-0.008 65
0.010 51
0.011 41
-0.010 31
Name: price_diff, dtype: int64
diff_group = result_df.groupby('price_diff').agg({ 'quantity_sum': 'mean'})
diff_group[(diff_group.index>0) & (diff_group.index<0.015)].plot(figsize=(10,5),grid=True);
ভলিউম মূল্য প্রভাব
একটি টিক পরিবর্তনের জন্য প্রয়োজনীয় ট্রেডিং ভলিউম আগে গণনা করা হয়েছিল, কিন্তু এটি সঠিক নয় কারণ এটি এমন ধারণার উপর ভিত্তি করে যে প্রভাব ইতিমধ্যেই ঘটেছে। এখন আসুন ট্রেডিং ভলিউম দ্বারা আনা মূল্যের প্রভাবের দিকে নজর দেওয়া যাক।
এখানে ডেটা 1 সেকেন্ডে নমুনা করা হয়, এবং প্রতি 100টি পরিমাণে 1 ধাপ হয় এবং এই পরিমাণের সীমার মধ্যে মূল্য পরিবর্তনগুলি গণনা করা হয়। কিছু মূল্যবান উপসংহার টানা হয়েছিল:
- যখন বাই অর্ডার ভলিউম 500 এর নিচে থাকে, তখন প্রত্যাশিত দামের পরিবর্তন হয়, যা প্রত্যাশার সাথে সঙ্গতিপূর্ণ হয়, দামকে প্রভাবিত করে।
- যখন ট্রেডিং ভলিউম কম হয়, তখন এটি একটি রৈখিক সম্পর্ক অনুসরণ করে, অর্থাৎ, ট্রেডিং ভলিউম যত বেশি হবে, মূল্য বৃদ্ধি তত বেশি হবে।
- ক্রয় অর্ডারের পরিমাণ যত বেশি হবে, দামের পরিবর্তন তত বেশি হবে, যা প্রায়শই মূল্যের অগ্রগতির প্রতিনিধিত্ব করে। অগ্রগতির পরে, দাম ফিরে আসতে পারে। নির্দিষ্ট বিরতিতে নমুনা সংগ্রহের সাথে মিলিত হলে, ডেটা অস্থির থাকে।
- আপনার স্ক্যাটার চার্টের উপরের প্রান্তে মনোযোগ দেওয়া উচিত, অর্থাৎ যে অংশে ট্রেডিং ভলিউম মূল্য বৃদ্ধির সাথে মিলে যায়।
- শুধুমাত্র এই ট্রেডিং পেয়ারের জন্য, ভলিউম এবং মূল্য পরিবর্তনের মধ্যে সম্পর্কের একটি মোটামুটি সংস্করণ দেওয়া হল:
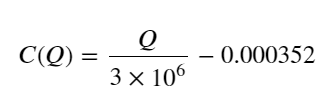
তাদের মধ্যে, “C” মূল্যের পরিবর্তনের প্রতিনিধিত্ব করে, এবং “Q” ক্রয় পরিমাণের প্রতিনিধিত্ব করে।
df_resampled = buy_trades.resample('1S').agg({
'price': ['first', 'last', 'count'],
'quantity': 'sum'
})
df_resampled['price_diff'] = round(df_resampled[('price', 'last')] - df_resampled[('price', 'first')],3)
df_resampled['price_diff'] = df_resampled['price_diff'].fillna(0)
result_df_raw = pd.DataFrame({
'price_diff': df_resampled['price_diff'],
'quantity_sum': df_resampled[('quantity', 'sum')],
'data_count': df_resampled[('price', 'count')]
})
result_df = result_df_raw[result_df_raw['price_diff'] != 0]
df = result_df.copy()
bins = np.arange(0, 30000, 100) #
labels = [f'{i}-{i+100-1}' for i in bins[:-1]]
df.loc[:, 'quantity_group'] = pd.cut(df['quantity_sum'], bins=bins, labels=labels)
grouped = df.groupby('quantity_group')['price_diff'].mean()
grouped_df = pd.DataFrame(grouped).reset_index()
grouped_df['quantity_group_center'] = grouped_df['quantity_group'].apply(lambda x: (float(x.split('-')[0]) + float(x.split('-')[1])) / 2)
plt.figure(figsize=(10,5))
plt.scatter(grouped_df['quantity_group_center'], grouped_df['price_diff'],s=10)
plt.plot(grouped_df['quantity_group_center'], np.array(grouped_df['quantity_group_center'].values)/2e6-0.000352,color='red')
plt.xlabel('quantity_group_center')
plt.ylabel('average price_diff')
plt.title('Scatter plot of average price_diff by quantity_group')
plt.grid(True)
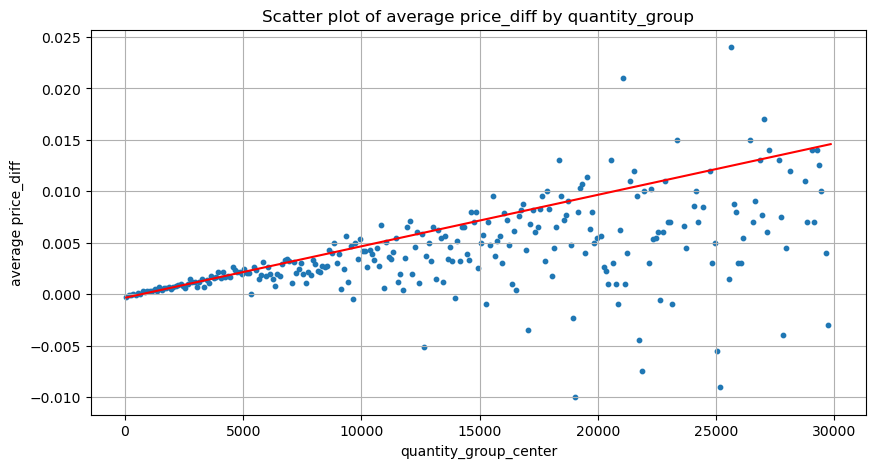
grouped_df.head(10)
| quantity_group | price_diff | quantity_group_center | |
|---|---|---|---|
| 0 | 0-199 | -0.000302 | 99.5 |
| 1 | 100-299 | -0.000124 | 199.5 |
| 2 | 200-399 | -0.000068 | 299.5 |
| 3 | 300-499 | -0.000017 | 399.5 |
| 4 | 400-599 | -0.000048 | 499.5 |
| 5 | 500-699 | 0.000098 | 599.5 |
| 6 | 600-799 | 0.000006 | 699.5 |
| 7 | 700-899 | 0.000261 | 799.5 |
| 8 | 800-999 | 0.000186 | 899.5 |
| 9 | 900-1099 | 0.000299 | 999.5 |
প্রাথমিক সর্বোত্তম অর্ডার অবস্থান
ট্রেডিং ভলিউমের মডেলিং এবং দামের প্রভাবের সাথে সামঞ্জস্যপূর্ণ ভলিউমের মোটামুটি মডেলের সাথে, সর্বোত্তম মুলতুবি অর্ডার অবস্থান গণনা করা সম্ভব বলে মনে হয়। আসুন কিছু অনুমান করা যাক এবং প্রথমে একটি দায়িত্বহীন সর্বোত্তম মূল্যের অবস্থান দিন।
- অনুমান করুন যে শক হওয়ার পরে মূল্যটি আসল মূল্যে ফিরে আসে (এটি অবশ্যই অসম্ভাব্য, এবং শকের পরে মূল্যের পুনর্বিশ্লেষণের প্রয়োজন হয়)
- অনুমান করুন যে এই সময়ের মধ্যে ট্রেডিং ভলিউম এবং অর্ডার ফ্রিকোয়েন্সি বিতরণ প্রিসেটের সাথে সামঞ্জস্যপূর্ণ (এটিও ভুল, এখানে এক দিনের মূল্য অনুমানের জন্য ব্যবহার করা হয়েছে, এবং লেনদেনের সুস্পষ্ট সমষ্টি রয়েছে)।
- অনুমান করুন যে সিমুলেশনের সময় শুধুমাত্র একটি বিক্রয় আদেশ ঘটে এবং তারপর অবস্থানটি বন্ধ হয়ে যায়।
- অনুমান করুন যে অর্ডারটি পূরণ হওয়ার পরে, অন্যান্য ক্রয় আদেশগুলি রয়েছে যা মূল্যকে বাড়িয়ে দেয়, বিশেষত যখন এই প্রভাবটি এখানে উপেক্ষা করা হয় এবং এটি কেবলমাত্র ধরে নেওয়া হয় যে এটি ফিরে আসবে৷
প্রথমে একটি সাধারণ প্রত্যাশিত রিটার্ন লিখুন, অর্থাৎ, সম্ভাব্যতা যে 1 সেকেন্ডের মধ্যে ক্রমবর্ধমান ক্রয় অর্ডারগুলি Q-এর চেয়ে বেশি, প্রত্যাশিত রিটার্ন দ্বারা গুণিত (অর্থাৎ প্রভাবের মূল্য):
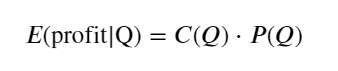
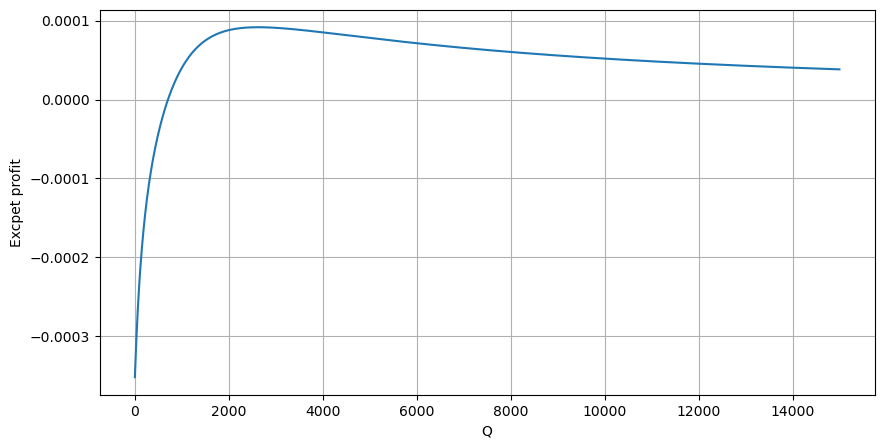
চিত্র অনুসারে, প্রত্যাশিত লাভ প্রায় 2500 সর্বোচ্চ, যা গড় আয়তনের প্রায় 2.5 গুণ। অর্থাৎ সেল অর্ডার 2500 এ স্থাপন করা উচিত। এটি আবার জোর দেওয়া দরকার যে অনুভূমিক অক্ষটি 1 সেকেন্ডের মধ্যে লেনদেনের পরিমাণকে উপস্থাপন করে এবং এটিকে গভীরতার অবস্থানের সাথে সহজভাবে সমান করা যায় না। এবং এটি এমন একটি সময় যখন এখনও গুরুত্বপূর্ণ গভীর তথ্যের অভাব রয়েছে এবং আমরা কেবলমাত্র ট্রেডের উপর ভিত্তি করে অনুমান করতে পারি।
সারসংক্ষেপ
এটি পাওয়া যায় যে বিভিন্ন সময়ের ব্যবধানে ট্রেডিং ভলিউমের বন্টন একক ট্রেডিং ভলিউমের বন্টনের একটি সহজ স্কেলিং। আমরা দামের প্রভাব এবং লেনদেনের সম্ভাবনার উপর ভিত্তি করে একটি সাধারণ প্রত্যাশিত রিটার্ন মডেলও তৈরি করেছি যদি বিক্রয়ের পরিমাণ কম হয়, তবে এটির জন্য একটি নির্দিষ্ট পরিমাণ প্রয়োজন লাভ মার্জিন আছে লেনদেনের পরিমাণ যত বেশি হবে, সম্ভাব্যতা তত কম হবে মাঝখানে একটি সর্বোত্তম আকার রয়েছে, যা কৌশলটি খুঁজছে। অবশ্যই, এই মডেলটি এখনও খুব সহজ, আমি পরবর্তী নিবন্ধে এটি সম্পর্কে কথা বলতে থাকব।
#1s内的累计分布
df_resampled = buy_trades['quantity'].resample('1S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]
depths = np.array(range(0, 15000, 10))
mean = df_resampled['quantity'].mean()
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2.05)
probabilities_s = np.array([((1+20**(-depth/mean))*depth/mean+1)**(alpha) for depth in depths])
profit_s = np.array([depth/2e6-0.000352 for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities_s*profit_s)
plt.xlabel('Q')
plt.ylabel('Excpet profit')
plt.grid(True)