In diesem Artikel werden wir einen Überblick über den Ornstein-Uhlenbeck-Prozess geben, die mathematischen Formeln beschreiben, ihn mit Python implementieren und simulieren und einige praktische Anwendungen in der Quantifizierung von Finanzen und Systemhandel diskutieren. Wir werden ein höher entwickeltes Modell für Zufallsprozesse verwenden, das als Ornstein-Uhlenbeck-Prozess (OU) bezeichnet wird und für die Modellierung von Recursion-Zeitfolgen verwendet werden kann, die ein Gleichwertigkeitsverhalten aufweisen. Es ist besonders nützlich für die Modellierung von Zinssätzen in Derivaten und die Durchführung von Algorithmen für Systemhandel beim Handel.

Was ist der Ornstein-Uhlenbeck-Prozess?

Die Ornstein-Uhlenbeck-Prozesse ist eine kontinuierliche zeitlich zufällige Prozedur, die zur Modellierung der Mittelwert-Rückgangshandlung verwendet wird. Das bedeutet, dass die OU-Prozesse im Gegensatz zu standardisierten Zufallswanderungen oder Brownian-Bewegungen, die unendlich weit abweichen können, oftmals im Laufe der Zeit zu einem langfristigen Mittelwert zurückkehren. Mathematisch gesehen ist die OU-Prozess die Lösung einer bestimmten Zufallsdifferenzierungsgleichung (SDE), die diese Mittelwert-Rückgangshandlung steuert.

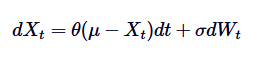
Xt ist der Zufallsprozess in der Zeit t, μ ist der langfristige Mittelwert, θ ist die Mittelwert-Rückkehrrate, δ ist die Schwankung und dWt ist der Wiener-Prozess oder die Standard-Brown-Bewegung.

Hintergrund und Anwendung

Der Ornstein-Uhlenbeck-Prozess wurde 1930 von Leonard Ornstein und George Eugene Uhlenbeck entwickelt, um die Geschwindigkeit von Teilchen zu simulieren, die unter Reibung eine Brownian-Bewegung ausüben. Im Laufe der Zeit haben sich seine Anwendungen weit über die physikalische Grenze hinaus entwickelt und finden Anwendung in verschiedenen Bereichen wie Biologie, Chemie, Wirtschaft und Finanzen.

In der Quantifizierung von Finanzen sind OU-Prozesse besonders nützlich, um die Phänomene der Mittelwertrückführung zu modellieren. Prominente Beispiele sind die Volatilität von Zinssätzen, Wechselkursen und Finanzmärkten. So ist beispielsweise das populäre Zinsmodell, das Vasicek-Modell, direkt aus OU-Prozessen abgeleitet.

Wichtig in der Quantitative Finanzwelt

Der Ornstein-Uhlenbeck-Prozess ist in der Quantifizierung von Finanzen von entscheidender Bedeutung, da seine regressive Eigenschaft die natürliche Wahl für die Modellierung von Finanzvariablen darstellt, die keine Zufallswanderung aufweisen, sondern um eine stabile langfristige Schwankung des Mittelwerts schwanken. Diese Eigenschaft ist für die Modellierung von Zinssätzen von entscheidender Bedeutung, bei der die regressive Eigenschaft der Mittelwerte den Einfluss der Zentralbank auf die langfristige Zinsstabilität widerspiegelt.

Darüber hinaus wird der OU-Prozess auch für Asset-Pricing-Modelle (einschließlich der Bewertung von Derivaten) und Risikomanagement-Strategien verwendet. Er kann auch als Baustein für komplexere Modelle dienen, wie das Cox-Ingersoll-Ross (CIR) -Modell, das den OU-Prozess zur Modellierung von Zinssätzen mit einem nicht-negativen Wert erweitert.

Wesentliche Merkmale und Intuition

Die Hauptmerkmale des Ornstein-Uhlenbeck-Prozesses lassen sich wie folgt zusammenfassen:

• Durchschnittliche Rückkehr:OU-Prozesse neigen dazu, zum langfristigen Mittelwert zurückzukehren. Das ist ein deutlicher Gegensatz zu Prozessen wie Brown-Bewegungen, die diese Tendenz nicht zeigen.
• Unbeständigkeit:Der Parameter δ ist die Stufe der Zufälligkeit oder Schwankungen im Prozess. Je höher die Schwankungen, desto größer ist die Abweichung des Prozesses vom Mittelwert vor der Rückkehr.
• Rückfahrt:Der Parameter θ bestimmt die Geschwindigkeit, mit der der Prozess zum Mittelwert zurückkehrt. Je höher der Wert θ, desto schneller wird der Mittelwert zurückgeführt.
• Stabilität:Die OU-Prozesse sind stabil, was bedeutet, dass ihre statistischen Eigenschaften sich nicht mit der Zeit ändern. Dies ist wichtig für die Modellierung stabiler Systeme im Finanzbereich.

Intuitiv betrachtet, kann man den Ornstein-Uhlenbeck-Prozess als Modellierung des Verhaltens der Schleimhaut betrachten, die sich um den Mittelwert ausdehnt. Während der Prozess durch zufällige Schwankungen vom Mittelwert abweichen kann, sorgt die Zugspitze der Schleimhaut (ähnlich der Mittelwertrückkehr) dafür, dass er schließlich zum Mittelwert zurückkehrt.

Vergleiche mit anderen Zufallsverfahren

Da der OU-Prozess eng mit der Modellierung verschiedener finanzieller Phänomene verbunden ist, wird er häufig mit anderen Zufallsprozessen verglichen (z. B. Brownian Bewegungen und geometrische Brownian Bewegungen (GBM)). Anders als bei Brownian Bewegungen (wobei Brownian Bewegungen keine Tendenz zur Rückkehr zum Mittelwert haben), weist der OU-Prozess eine deutliche Mittelwert-Rückkehr-Bewegung auf. Dies macht ihn für die Modellierung von Szenarien mit variablen Schwankungen um eine stabile Gleichgewichtsbewegung geeignet.

Im Gegensatz zu GBM, das normalerweise für die Modellierung von Aktienpreisen verwendet wird und Drift- und Fluktuationsfaktoren enthält, zeigt der OU-Prozess kein Indexwachstum, sondern eine Schwingung um seinen Durchschnittswert. GBM ist besser geeignet, um Zahlen zu modellieren, die mit der Zeit ansteigen, während der OU-Prozess sehr gut geeignet ist, um Variablen zu modellieren, die ein Rückgang des Durchschnittswertes aufweisen.

Beispiele für Quantitative Finanzen

Der Ornstein-Uhlenbec-Prozess ist in der Finanzwelt weit verbreitet, insbesondere in Modellierungsszenarien mit der Mittelwert-Rückkehr als Schlüsselfunktion. Im Folgenden werden einige der am häufigsten verwendeten Anwendungsfälle diskutiert.

Zinsmodellierung

Eine der prominentesten Anwendungen des OU-Prozesses ist die Modellierung von Zinssätzen, insbesondere im Rahmen des Vasicek-Modells. Das Vasicek-Modell geht davon aus, dass Zinssätze dem OU-Prozess folgen, d. h. dass Zinssätze tendenziell im Laufe der Zeit zu langfristigen Durchschnittswerten zurückkehren. Diese Eigenschaft ist von entscheidender Bedeutung, um das Verhalten von Zinssätzen genau zu simulieren, da Zinssätze tendenziell nicht unbegrenzt schwanken, sondern in der Nähe von Durchschnittswerten, die von wirtschaftlichen Bedingungen beeinflusst werden.

Vermögenspreis

In der Pricing von Vermögenswerten, insbesondere von Fixed-Earnings-Sicherheiten, wird der OU-Prozess häufig verwendet, um die Entwicklung der Rendite von Anleihen zu simulieren. Die mittlere Rücklaufart des OU-Prozesses stellt sicher, dass die Rendite nicht zu weit von ihrem historischen Durchschnittswert abweicht, was mit dem beobachteten Marktverhalten übereinstimmt. Dies macht den OU-Prozess zu einem wertvollen Werkzeug für die Pricing von Anleihen und anderen zinssensiven Instrumenten.

Pairing-Handelsstrategien

Pairing Trading ist eine marktneutrale Strategie, bei der es darum geht, eine Offset-Position in zwei verwandten Vermögenswerten aufzubauen. In diesem Fall ist der OU-Prozess besonders nützlich, da er die Preisunterschiede zwischen den beiden Vermögenswerten modellieren kann, wobei die Preisunterschiede in der Regel eine Durchschnittswertrückkehr sind. Durch die Modellierung der Preisunterschiede mit dem OU-Prozess kann der Händler die Ein- und Ausstiegspunkte für den Gewinn bestätigen, wenn der Preis von seinem Durchschnittswert abweicht, und die Rückkehr zum Durchschnittswert prognostizieren, wodurch ein Handelssignal erzeugt wird.

Wenn beispielsweise die Preisunterschiede zwischen zwei Futures über einen gewissen Wertverlust hinausgewachsen sind, kann der Händler die gut funktionierenden Futures abschneiden und die schlecht funktionierenden Futures verkaufen, in der Erwartung, dass die Preisunterschiede zu ihrem historischen Durchschnitt zurückkehren, um bei einer Umkehrung zu profitieren.

Lösung der Ornstein-Uhlenbeck SDE

Die differentielle Gleichung des Ornstein-Uhlenbeck-Prozesses ist die Grundlage für die Lösung. Um diese SDE zu lösen, verwenden wir die Integrationsfaktoren.

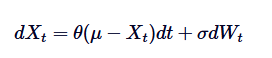
Zuerst multiplizieren wir beide Seiten mit dem Integralfaktor /upload/asset/28dfe9abfb54772651590.png:

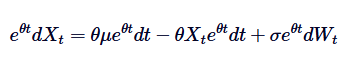
Bitte beachten Sie, dass die Differenz auf der linken Seite als Multiplikator dargestellt werden kann, wenn wir auf beiden Seiten 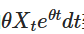hinzufügen:

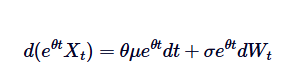
Wenn wir beide Seiten von 0 bis t integrieren, erhalten wir:

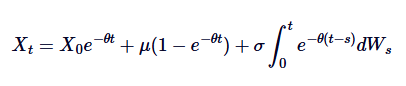
Das ist die allgemeine Definition der Ornstein-Uhlenbeck SDE.

Die oben beschriebene eindeutige Lösung hat mehrere wichtige Bedeutungen. Der erste Teil 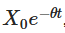zeigt, dass der Anfangswert mit der Zeit abnimmt und wie der Prozess allmählich seinen Anfangspunkt vergisst. Der zweite Teil 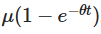zeigt, dass der Prozess mit der Zeit zu einem Durchschnittswert von μ fällt.

Diese Lösung betont die Balance zwischen dem Regressionsverhalten des Mittelwerts der Bestimmtheit und dem Brownian-Bewegung-getriebenen Zufallsanteil. Ein Verständnis dieser Lösung ist entscheidend für die effektive Simulation der OU-Prozesse, wie unten beschrieben.

Verbindungen zu anderen Zufallsvorgängen

Die Ornstein-Uhlenbeck-Prozesse haben einige wichtige Verbindungen zu anderen bekannten Zufallsprozessen (einschließlich der Brown-Bewegung und dem Vasicek-Modell).

Beziehung zur Brown-Bewegung

Der Ornstein-Uhlenbeck-Prozess kann als die Mittelwert-Rückkehr-Version der Brownian Bewegung betrachtet werden. Die Brownian Bewegung beschreibt einen Prozess, der eine Tendenz hat, die unabhängig von der Zunahme und ohne Rückkehr des Mittelwertes ist, während der OU-Prozess die Mittelwert-Rückkehr durch die Verwendung von Drift-Kriterien modifiziert, um die Brownian Bewegung einzuführen, wodurch der Prozess in den Mittelwert zurückgezogen wird. Mathematisch gesehen wird der OU-Prozess auf die Standard-Brownian Bewegung reduziert, wenn wir dieθ = 0 setzen:

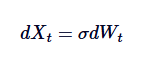
Die Brown-Bewegung ist also ein besonderes Beispiel für ein OU-Verfahren, das auf die Abwesenheit der Mittelwert-Rückkehr entspricht.

Beziehung zum Vasicek-Modell

Das Vasicek-Modell ist eine weit verbreitete Methode zur Modellierung von Zinssätzen und ist im Wesentlichen eine Anwendung des Ornstein-Uhlenbeck-Prozesses in der Zinsentwicklung. Das Vasicek-Modell nimmt an, dass die Zinssätze dem OU-Prozess folgen, wobei die SDE definiert ist als:

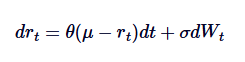
Dort ist rt für kurzfristige Zinssätze, wobei die Interpretation der Parameter θ, μ und δ ähnlich ist wie bei der OU-Prozess-Interpretation. Die Fähigkeit des Vasicek-Modells, einen Mittelwert-Rückkehr-Zinssatz-Pfad zu erzeugen, ist einer seiner Hauptvorteile in der Finanzmodellierung.

Ein Verständnis dieser Zusammenhänge ermöglicht ein breiteres Verständnis der Verwendung der OU-Prozesse in verschiedenen Umgebungen, insbesondere im Finanzbereich. Die praktische Bedeutung dieser Zusammenhänge wird im Folgenden bei der Erörterung von Anwendungsbeispielen erörtert.

Ornstein-Uhlenbeck-Prozess mit Python simuliert

In diesem Abschnitt werden wir untersuchen, wie man die Ornstein-Uhlenbeck-OU-Prozesse mit Python simuliert. Dies beinhaltet die Euler-Maruyama-Aussonderung zur Aussonderung der Zufalls-Definierung der OU-Prozesse (SDE).

Die Zersplitterung der SDE

Lassen Sie uns die oben genannten mathematischen Formeln der SDE noch einmal durchgehen und die einzelnen Begriffe zusammenfassen:

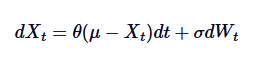
In,

• Xt ist der Wert des Prozesses in der Zeit t.
• θ ist die Geschwindigkeit der Mittelwertrückführung.
• μ ist der langfristige Durchschnitt des Prozesses.
• δ ist das Parameter der Schwankungsrate.
• dWt ist die Inkrementation des Wiener-Prozesses (Standard-Brown-Bewegung).

Um diesen Prozess am Computer zu simulieren, benötigen wir eine Dispergierung des kontinuierlichen Zeit-SDE. Eine häufig verwendete Methode ist die Euler-Maruyama-Dispergierung, die einen kontinuierlichen Prozess annähert, indem man die kleinen Schritte der Dispergierung 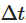berücksichtigt. Die Dispergierungsform des Ornstein-Uhlenbeck-Prozesses ist wie folgt:

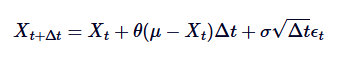
Dabei ist 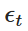eine zufällige Variable, die aus der normalen normalen Standardverteilung abgezogen wurde (d.h. 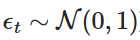). Diese Dispersion ermöglicht es uns, die Werte von Xt mit der Zeit zu berechnen und so das Verhalten des OU-Prozesses zu simulieren.

Python-Implementierung

Lassen Sie uns nun den Ornstein-Uhlenbeck-Prozess in Python dezentralisieren. Im Folgenden verwenden wir nur die NumPy- und Matplotlib-Python-Bibliotheken.

Zuerst importieren wir NumPy und Matplotlib in der Standardform. Dann geben wir alle Parameter für das OU-Modell an. Danach weisen wir ein NumPy-Array mit einer Länge von N vor, um es nach der Berechnung des OU-Pfades hinzuzufügen. Dann iterieren wir N-1 (Schritt 1 ist die angegebene Anfangsbedingung X0), simulieren den Zufallszuwachs dW, und berechnen dann die nächste iteration des OU-Pfades nach der obigen mathematischen Formel.

import numpy as np
import matplotlib.pyplot as plt

# Parameters for the OU process
theta = 0.7      # Speed of mean reversion
mu = 0.0         # Long-term mean
sigma = 0.3      # Volatility
X0 = 1.0         # Initial value
T = 10.0         # Total time
dt = 0.01        # Time step
N = int(T / dt)  # Number of time steps

# Pre-allocate array for efficiency
X = np.zeros(N)
X[0] = X0

# Generate the OU process
for t in range(1, N):
    dW = np.sqrt(dt) * np.random.normal(0, 1)
    X[t] = X[t-1] + theta * (mu - X[t-1]) * dt + sigma * dW

# Plot the result
plt.plot(np.linspace(0, T, N), X)
plt.title("Ornstein-Uhlenbeck Process Simulation")
plt.xlabel("Time")
plt.ylabel("X(t)")
plt.show()

Das Ergebnis ist wie folgt:

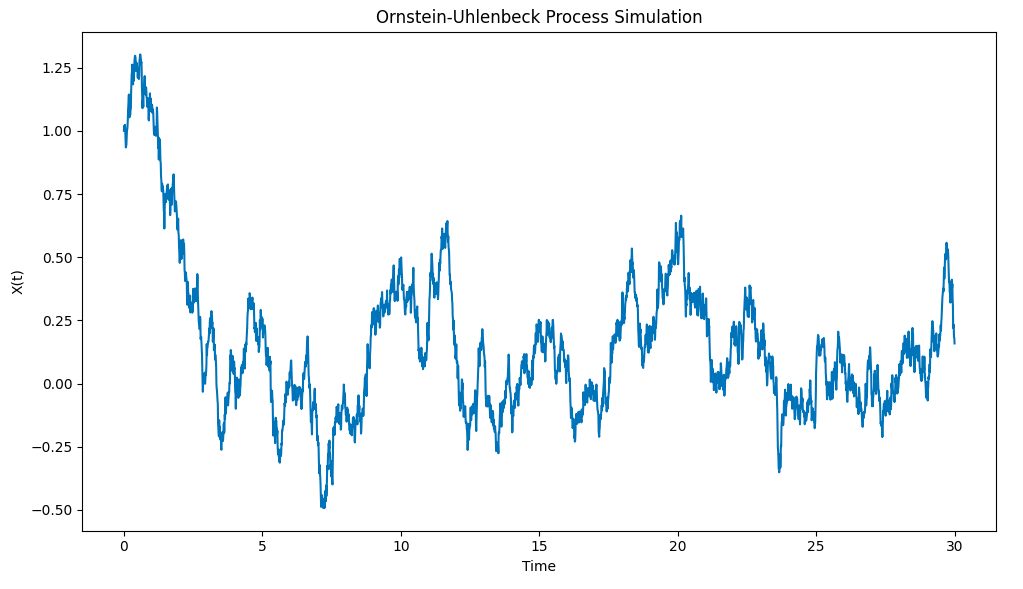
Ornstein-Uhlenbeck-Prozess-Simulation mit Python

Beachten Sie, wie der Prozess schnell von der Ausgangsbedingung X0 = 1 zum Mittelwert μ = 0 zieht und dann, wenn er von diesem Mittelwert abweicht, eine Tendenz zeigt, zu diesem Mittelwert zurückzukehren.

Zusammenfassung und weitere Schritte

In diesem Artikel beschreiben wir den Ornstein-Uhlenbeck-Prozess, beschreiben seine mathematischen Formeln und bieten eine grundlegende Implementierung in Python, um eine dezentrale Version des Continuous-Time-SDE zu simulieren. In den folgenden Artikeln werden wir die komplexeren SDE, die auf dem OU-Prozess basieren, untersuchen und sehen, wie sie für Systemhandel und Derivaten-Pricing-Anwendungen verwendet werden.

Vollständiger Code

# OU process simulation

import numpy as np
import matplotlib.pyplot as plt

# Parameters for the OU process
theta = 0.7      # Speed of mean reversion
mu = 0.0         # Long-term mean
sigma = 0.3      # Volatility
X0 = 1.0         # Initial value
T = 30.0         # Total time
dt = 0.01        # Time step
N = int(T / dt)  # Number of time steps

# Pre-allocate array for efficiency
X = np.zeros(N)
X[0] = X0

# Generate the OU process
for t in range(1, N):
    dW = np.sqrt(dt) * np.random.normal(0, 1)
    X[t] = X[t-1] + theta * (mu - X[t-1]) * dt + sigma * dW

# Plot the result
plt.plot(np.linspace(0, T, N), X)
plt.title("Ornstein-Uhlenbeck Process Simulation")
plt.xlabel("Time")
plt.ylabel("X(t)")
plt.show()

Der Grund für die Veröffentlichung des Artikels ist die Übertragung von Quantify auf Python.