Lassen Sie uns darüber sprechen, wie die Parameter mehrerer programmatischer Handelsmodelle optimiert werden können

• #### Parameterhochland und Parameterinsel

　 Ein wichtiges Prinzip bei der Parameteroptimierung ist es, Parameterhöhen und nicht Parameterinseln anzusprechen. Ein so genannter Parameterhöhen bedeutet, dass es einen breiteren Parameterbereich gibt, in dem das Modell bessere Ergebnisse erzielt. Im Allgemeinen wird mit dem Zentrum des Hochlands eine annähernd normale Verteilung gebildet. Ein so genannter Parameterinsel bedeutet, dass das Modell nur dann gut funktioniert, wenn die Parameterwerte in einem sehr kleinen Bereich liegen, und die Leistung des Modells wird deutlich verändert, wenn die Parameter von diesem Wert abweichen.

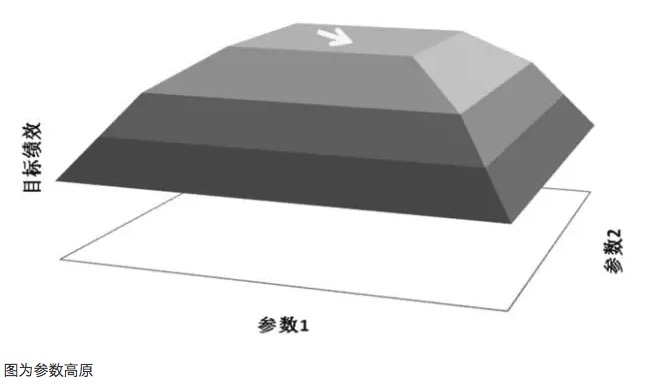
• #### Grafik als Parameterhochland

Nehmen wir das Beispiel eines Parameter-Hochland-Diagramms und eines Parameter-Insel-Diagramms. Angenommen, in einem Handelsmodell gibt es zwei Parameter, Parameter 1 und Parameter 2, die nach einer Umlaufprüfung mit den beiden Parametern eine dreidimensionale Performance-Diagramm erhalten. Eine gute Parameterverteilung sollte die Parameter-Hochland-Diagramm sein, so dass die profitable Performance des Modells auch dann gewährleistet ist, wenn die Einstellungen der Parameter verschoben sind.

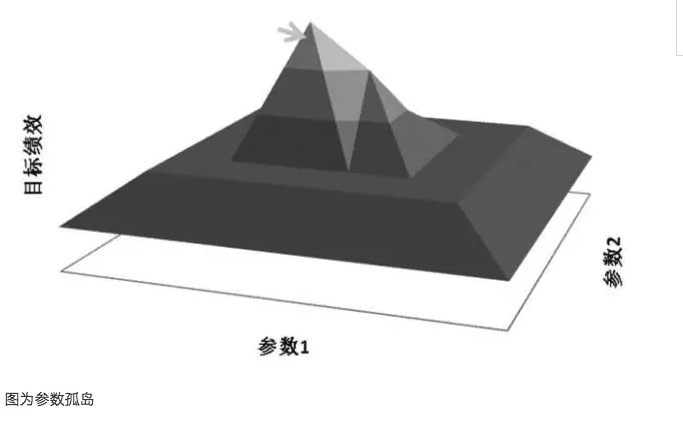
In der Regel ist es möglich, dass der optimale Parameter ein Ergebnis einer Übersummierung ist, wenn die Leistung eines Systems von nahegelegenen Parametern weit von der Leistung des optimalen Parameters abweicht. In der Mathematik kann er als eine Singularitätslösung betrachtet werden, anstatt als die Lösung mit den größten Werte, die gesucht werden soll.

Eine Überübereinstimmung hängt mit dem ausgewählten Muster zusammen, wenn das ausgewählte Muster nicht die Gesamtmerkmale des Marktes repräsentiert und die Parameter nur so angepasst werden, dass die Testergebnisse einen positiven Erwartungswert erreichen, was zweifellos eine Selbsttäuschung ist. Die erhaltene Parameterwerte sind die unwirksamen Parameterwerte der Überübereinstimmung.

Der Hauptwiderspruch zwischen Überpassung und Parameteroptimierung besteht darin, dass die optimalen Parameter, die mit der Optimierung von Modellparametern erzielt werden, nur auf einer historischen Datensammlung basieren, die bereits stattgefunden hat, während die zukünftige Entwicklung sich dynamisch verändert und sowohl Ähnlichkeiten als auch Unterschiede gegenüber der historischen Entwicklung aufweist. Der Modelldesigner kann die Parameter finden, mit denen die Modelle in der Geschichte am besten abschneiden, aber diese Parameter sind nicht unbedingt die besten in der tatsächlichen Anwendung des zukünftigen Modells, und noch besser, die historisch besten Modellparameter, die in der zukünftigen Modellkrieg schlecht abschneiden und sogar erhebliche Verluste verursachen können.

Darüber hinaus ist die Parameterhöhe und die Parameterinsel häufig auch mit der Anzahl der Transaktionen verbunden. Wenn die Anzahl der Transaktionen des Modells geringer ist, kann oft ein geeigneter Parameterpunkt gefunden werden, so dass das Modell bei allen Transaktionen profitiert. Diese Parameteroptimierung des Modells zeigt eine stärkere Zufälligkeit.

• #### Optimierungsmethoden

Nach dem Verständnis von Parameterhöhen und Parameterinseln ist die Optimierung der Parameter sehr wichtig, insbesondere wenn mehrere Parameter in einem Modell vorhanden sind (sogenannte Parameterarrays). Häufig beeinflusst der Wert eines Parameters die Verteilung eines anderen Parameterhöhen. Wie kann man dann die Parameterarrays optimieren?

Eine Methode ist die schrittweise Annäherung: 1. Optimieren Sie einen Parameter einzeln, erhalten Sie den besten Wert, der fest ist, und 2. Optimieren Sie einen anderen Parameter, erhalten Sie den besten Wert, der fest ist. So läuft der Kreislauf, bis die Optimierung nicht mehr verändert wird. Zum Beispiel, ein linearer Crossover-Kauf- und Verkaufsmodell, zwei unabhängige Parameter sind die mittlere kurze Periode N1 und die lange Periode N2. Zuerst wird N2 als 1 festgelegt, N1 wird im Bereich von 1 bis 100 getestet und gefiltert, um den besten Wert zu finden.

Eine andere Methode besteht darin, mithilfe einer programmierbaren Software-Design-Plattform mit leistungsfähigen Rechenfunktionen die Verteilung zwischen der Zielfunktion und den Arrays von Parametern direkt zu berechnen, dann die Verteilung der Multidimensionalen Differenz zu ermitteln und eine Differenz-Threshold zu definieren, bei der der Differenz-Absolute-Wert kleiner als der entsprechende Multidimensional-Volumen- und Multidimensionalschnitt-Radius ist, der als der stabilste Parameterwert gewählt wird.

Neben der Methode der Parameteroptimierung ist auch die Datensampelung ein wichtiger Faktor. Modelle, die Trend-Tracking als Handelsgedanken verwenden, sind besser in Trendbewegungen, Strategien, die Hoch- und Niedrigkauf als Handelsgedanken verwenden, sind besser in Schwankungsbewegungen. Daher ist es notwendig, bei der Parameteroptimierung die Bewegungen, die mit den Handelsgedanken übereinstimmen, angemessen zu entfernen, um Gewinne zu berücksichtigen, und die Bewegungsdaten, die nicht mit den Strategien übereinstimmen, zu erhöhen, um Verluste zu berücksichtigen.

Wenn man zum Beispiel die Aktienindex-Futures betrachtet, die zu Beginn der Börsengänge im Jahr 2010 und in der zweiten Hälfte des Jahres 2014, als die extremen bullish-Markt-Zustände auftraten, sind Aktienindex-Futures einseitig. Zweifellos werden alle Trendmodelle gute Ergebnisse erzielen. Wenn wir jedoch auch diese extremen Trenddaten in die Stichprobe einbinden, um die Parameter zu optimieren, sind die Modellparameter nicht unbedingt die besten.

Angenommen, ein Modell hat zwei Parameter: Parameter A, dessen Testergebnisse in einer einseitigen Zeitspanne sehr gut funktionieren und in anderen Zeitspannen generell funktionieren; Parameter B, dessen Testergebnisse in einer einseitigen Zeitspanne weniger gut funktionieren als Parameter A, der in anderen Zeitspannen besser funktioniert als Parameter A, und dessen Verteilung zwischen den Zeitspannen gleichmäßig ist. Auch wenn Parameter A in der gesamten Stichproben-Datenbank mit einem kombinierten Indikator wie Risiko-Gewinn höher als Parameter B getestet wird, sind wir eher geneigt, Parameter B zu verwenden, da Parameter B relativ stabiler ist und nicht auf eine bestimmte Stichprobe angewiesen ist.

Zusammenfassend lässt sich sagen, dass bei der Konstruktion von programmierten Handelsmodellen einerseits die Optimierung der Parameter die Modelle verbessern kann, um sie besser an die Modelle der Preisschwankungen anzupassen und die Investitionserträge zu erhöhen, und andererseits die Überanpassung an die Parameteroptimierung verhindert werden muss, was zu einer erheblichen Verringerung der Anwendbarkeit des Modells für die Veränderung der Marktlage führt.

Veröffentlicht von Programmierte Händler