Interessantes Verständnis von Naive Bayes

NavieBayes

  Es gibt viele Situationen, in denen Klassifizierung benötigt wird, wie z.B. die Klassifizierung von Nachrichten, die Klassifizierung von Patienten usw. In diesem Artikel wird ein einfacher, häufig verwendeter Klassifizierungsalgorithmus, der mit der praktischen Anwendung beginnt, vorgestellt.

• 01 Ein Beispiel für die Klassifizierung von Patienten

Lassen Sie mich mit einem Beispiel anfangen, und Sie werden sehen, dass der Bayesianer Klassifikator sehr gut verstanden wird, es ist nicht schwer. In einem Krankenhaus wurden am Morgen sechs Patienten aufgenommen, wie in der folgenden Tabelle gezeigt.

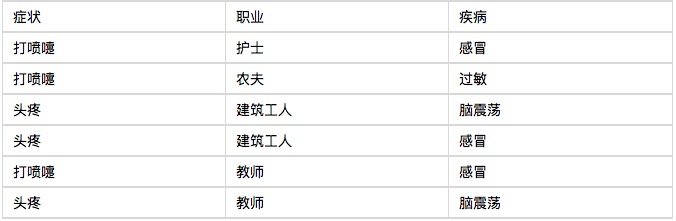
Nun kommt der siebte Patient, ein Bauarbeiter, der niest. Wie hoch ist die Wahrscheinlichkeit, dass er eine Erkältung hat?

  P(A|B) = P(B|A) P(A) / P(B)

Das kann sein:

  P(感冒|打喷嚏x建筑工人) 
  　　　　= P(打喷嚏x建筑工人|感冒) x P(感冒) 
  　　　　/ P(打喷嚏x建筑工人)

Angenommen, die beiden Eigenschaften “Sprühen” und “Bauherr” sind unabhängig voneinander, so wird die obige Gleichung zu

  P(感冒|打喷嚏x建筑工人) 
  　　　　= P(打喷嚏|感冒) x P(建筑工人|感冒) x P(感冒)
  　　　　/ P(打喷嚏) x P(建筑工人)

Das ist berechenbar.

  P(感冒|打喷嚏x建筑工人) 
  　　　　= 0.66 x 0.33 x 0.5 / 0.5 x 0.33 
  　　　　= 0.66

Die Wahrscheinlichkeit, dass der Patient eine Allergie oder einen Schlaganfall hat, kann ebenfalls berechnet werden. Durch Vergleich dieser Wahrscheinlichkeiten lässt sich herausfinden, welche Krankheit am wahrscheinlichsten auf ihn zukommt.

Das ist die grundlegende Methode des Bayesian Classifiers: Auf der Grundlage von statistischen Daten berechnen Sie die Wahrscheinlichkeit der einzelnen Kategorien anhand bestimmter Merkmale, um eine Klassifizierung zu erreichen.

• 02 Formeln für naive Bayesianer

Angenommen, ein Individuum hat n Eigenschaften (Feature), die als F1, F2, … und Fn gelten. Es gibt m Kategorien (Category), die als C1, C2, … und Cm gelten. Ein Bayesianer Klassifikator ist die Klassifizierung, die mit der größten Wahrscheinlichkeit berechnet wird.

  P(C|F1F2...Fn) 
  　　   = P(F1F2...Fn|C)P(C) / P(F1F2...Fn)

Da P ((F1F2…Fn) für alle Kategorien gleich ist, kann es weggelassen werden, und die Frage wird zu

  P(F1F2...Fn|C)P(C)

Maximaler Wert

Ein einfacher Bayesianer geht noch weiter und nimmt an, dass alle Merkmale voneinander unabhängig sind und daher

  P(F1F2...Fn|C)P(C) 
  　　   = P(F1|C)P(F2|C) ... P(Fn|C)P(C)

Jede Elemente der rechten Seite der Gleichung können aus der Statistik gewonnen werden, um die Wahrscheinlichkeit zu berechnen, dass jede Kategorie entspricht, und somit die Kategorie mit der höchsten Wahrscheinlichkeit zu finden.

Obwohl die Annahme, dass alle Merkmale voneinander unabhängig sind, in der Realität unwahrscheinlich ist, kann sie die Berechnung erheblich vereinfachen, und es gibt Studien, die zeigen, dass sie die Genauigkeit der Klassifikationsergebnisse nicht beeinflussen.

Im Folgenden werden zwei weitere Beispiele für den Einsatz eines einfachen Bayesian Classifiers gegeben.

• 03 Klassifizierung der Konten

Laut einer Stichprobe einer Community-Website sind 89% der 10.000 Accounts auf dieser Seite echte Accounts (setzen Sie auf C0) und 11% sind Fake Accounts (setzen Sie auf C1). Anschließend wird die Authentizität eines Accounts anhand von Statistiken beurteilt.

  C0 = 0.89 C1 = 0.11

Angenommen, ein Konto hat drei Eigenschaften: F1: Anzahl der Tage/Nachrichten F2: Anzahl der Freundschaften/Anmeldungstage F3: Sollte ein echtes Header verwendet werden (echtes Header ist 1, nicht echtes Header ist 0)? F1 = 0.1  F2 = 0.2  F3 = 0

Die Methode besteht darin, einen einfachen Bayesianer zu verwenden, um die Werte der folgenden Berechnungsformel zu berechnen:

P(F1|C)P(F2|C)P(F3|C)P©

Obwohl die obigen Werte aus Statistiken stammen, gibt es hier ein Problem: F1 und F2 sind kontinuierliche Variablen, und es ist nicht sinnvoll, die Wahrscheinlichkeit nach einem bestimmten Wert zu berechnen. Ein Trick ist, die Wahrscheinlichkeit eines Intervalls zu berechnen, indem man die kontinuierlichen Werte in die discreten Werte umwandelt.[0, 0.05]、(0.05, 0.2)、[0.2, +∞] drei Bereiche, dann berechne die Wahrscheinlichkeit für jeden Bereich. In unserem Beispiel ist F1 gleich 0.1, fällt in den zweiten Bereich, also berechne ich die Wahrscheinlichkeit für den zweiten Bereich.

Laut der Statistik:

P(F1|C0) = 0.5, P(F1|C1) = 0.1  P(F2|C0) = 0.7, P(F2|C1) = 0.2  P(F3|C0) = 0.2, P(F3|C1) = 0.9

Deshalb

P(F1|C0) P(F2|C0) P(F3|C0) P(C0)  = 0.5 x 0.7 x 0.2 x 0.89  = 0.0623 P(F1|C1) P(F2|C1) P(F3|C1) P(C1)  = 0.1 x 0.2 x 0.9 x 0.11  = 0.00198 Wie man sehen kann, hat dieser Benutzer zwar kein echtes Image, aber die Wahrscheinlichkeit, dass er ein echtes Konto ist, ist mehr als 30-mal höher als die Wahrscheinlichkeit, dass es ein gefälschtes Konto ist.

• 04 Klassifizierung nach Geschlecht

Im Folgenden finden Sie eine Reihe von Statistiken über menschliche Körpermerkmale.

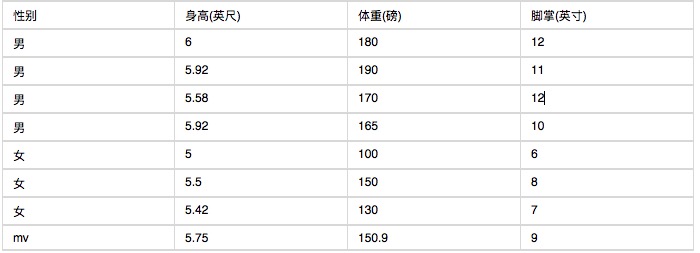
Wenn Sie wissen, dass eine Person 6 Fuß groß, 130 Pfund schwer und 8 Zentimeter groß ist, fragen Sie bitte, ob diese Person ein Mann oder eine Frau ist. Berechnen Sie die Werte der folgenden Formel nach dem simplen Bayes-Klassifikator.

P (Höhe und Geschlecht) x P (Gewicht und Geschlecht) x P (Fuss und Fuß und Geschlecht) x P (Geschlecht)

Die Schwierigkeit besteht darin, dass die Wahrscheinlichkeiten nicht in Abständen berechnet werden können, da die Höhe, das Gewicht und die Handflächen kontinuierliche Variablen sind. Da die Stichproben zu klein sind, können sie auch nicht in Abständen berechnet werden. Was ist zu tun?

Mit diesen Daten kann man die Klassifizierung nach Geschlecht berechnen.

P (Höhe=6 Jahre alt) x P (Gewicht=130 Jahre alt) x P (Fuss=8 Jahre alt) x P (Mann)

= 6.1984 x e-9

P (Höhe = 6 Mädchen) x P (Gewicht = 130 Mädchen) x P (Fussflächen = 8 Mädchen) x P (Frau)

= 5.3778 x e-4

Wie man sieht, ist die Wahrscheinlichkeit, dass es sich um eine Frau handelt, fast 10.000 Mal höher als bei einem Mann.

Weibo-Publikumsnummer aus dem Gipfel von Weibo