Intuitives Verständnis der Kointegration

Anleitung: Dieser Artikel soll Ihnen das Konzept der Integration auf eine intuitive Weise vorstellen und Ihnen helfen, die grundlegenden Bedeutungen, die Motive für das Konzept und die einfachen Anwendungsfälle zu verstehen.

• Zusammenfassung

Ich möchte hier nur darauf hinweisen, dass die intuitive Definition von Integration keine strengen mathematischen Symboldefinitionen und keine strengen Formel-Entwicklungen beinhaltet.

Wenn Sie interessiert sind, können Sie sich Wikipedia Cointegration anschauen.

Warum die Gleichgewicht/Kohärenz

Wenn es um die Integration geht, muss es um die Gleichmäßigkeit gehen.

Einfach ausgedrückt, ist die Planarität (Stationarität) eine Eigenschaft einer Sequenz, die im Laufe der Zeit unverändert bleibt, eine Eigenschaft, die uns sehr am Herzen liegt, wenn wir analytische Vorhersagen über die Daten machen. Wenn ein Satz von Zeitreihendaten planar ist, bedeutet dies, dass seine Mittelwerte und Differenzen unverändert bleiben, so dass wir einige statistische Techniken bequem auf die Sequenz anwenden können.

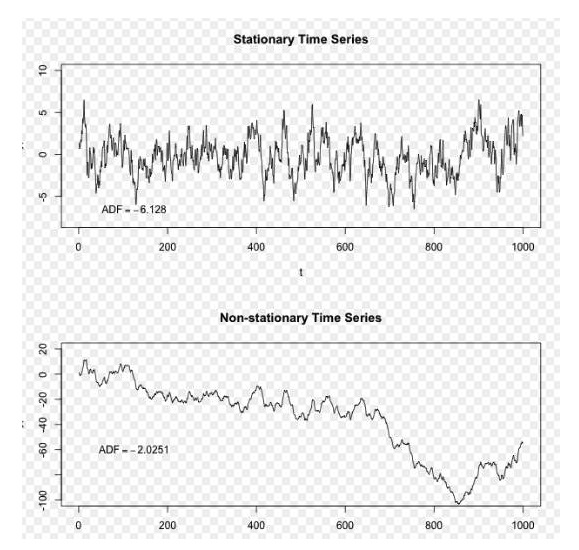
Bild von Wikipedia

In der obigen Grafik ist die oberste Sequenz eine gleichmäßige Sequenz, die wir sehen, dass sie immer um einen langfristigen Mittelwert schwankt, und die unterste Sequenz ist eine ungleichmäßige Sequenz, die wir sehen, dass ihr langfristiger Mittelwert wechselt.

Ein Beispiel für eine Anwendung: Wenn die Preisfolge eines Vermögenswertes (oder die Differenz zwischen zwei Preisen) stabil ist, kann man erwarten, dass der Preis zu einem bestimmten Zeitpunkt in der Zukunft zu diesem Mittelwert zurückkehrt, nachdem er von seinem Mittelwert abweicht. Wir können diese Eigenschaft nutzen, um zu investieren und damit zu profitieren. Nehmen wir an, dass der langfristige Mittelwert einer Aktie 9 US-Dollar ist, während der aktuelle Wert 8 US-Dollar ist.

Das ist eine Reihe von Aktienkursen mit gleichbleibender Natur:

Wenn zwei Gruppen von Sequenzen nicht gleichmäßig sind, aber ihre lineare Kombination eine gleichmäßige Sequenz ergeben kann, dann sagen wir, dass diese beiden Gruppen von Sequenzdaten integriert sind, und wir können die statistischen Eigenschaften auch auf die Sequenz dieser Kombination anwenden. Es muss jedoch darauf hingewiesen werden, dass eine Integrierung keine Korrelation ist.

Wenn beispielsweise die Differenz zwischen zwei Gruppen von Zeitreihendaten gleich ist, können wir aufgrund dieser Differenz einen Investitionsgewinn erzielen: Wenn die Preise der beiden Aktien zu unterschiedlich sind, erwarten wir aufgrund der Gleichheit, dass sich die Preisunterschiede annähern, und kaufen daher niedrigpreisige Aktien, verkaufen preisgekrönte Aktien und warten, bis der Preis zurückkehrt, um so einen Gewinn zu erzielen.

Das ist der Ursprung des Pairs Trading.

• Stabilität und Prüfverfahren

Streng genommen kann man die Gleichgewichtigkeit in zwei Arten unterteilen: streng stationär (strictly stationary) und schwach stationär (weak stationary). Die strenge Gleichgewichtigkeit bezieht sich darauf, dass eine Sequenz stets eine unveränderliche Verteilungsfunktion aufweist, während die schwache Gleichgewichtigkeit auf eine beschreibende Statistik mit einer unveränderlichen Konstante der Sequenz bezieht. Alle starken Gleichgewichtigkeitssequenzen erfüllen die Eigenschaft der schwachen Gleichgewichtigkeit, aber das Gegenteil gilt nicht. Was wir im Allgemeinen mit Gleichgewichtigkeit bezeichnen, ist schwache Gleichgewichtigkeit.

Ein Beispiel für eine Anwendung

Zunächst ist darauf hinzuweisen, dass eine Korrelation keine Korrelation ist. Wir konstruieren künstlich zwei Datensätze, um die Korrelation intuitiv zu betrachten. import numpy as np import pandas as pd import seaborn import statsmodels import matplotlib.pyplot as plt from statsmodels.tsa.stattools import coint

Konstruktionsdaten

Zuerst bauen wir zwei Datensätze mit einer Länge von 100 auf. Die erste Gruppe besteht aus 100 plus ein Abwärtstrendpunkt plus eine Standard-Normal-Verteilung. Die zweite Gruppe besteht aus 30 auf der Grundlage der ersten Gruppe, plus eine zusätzliche Standard-Normal-Verteilung.

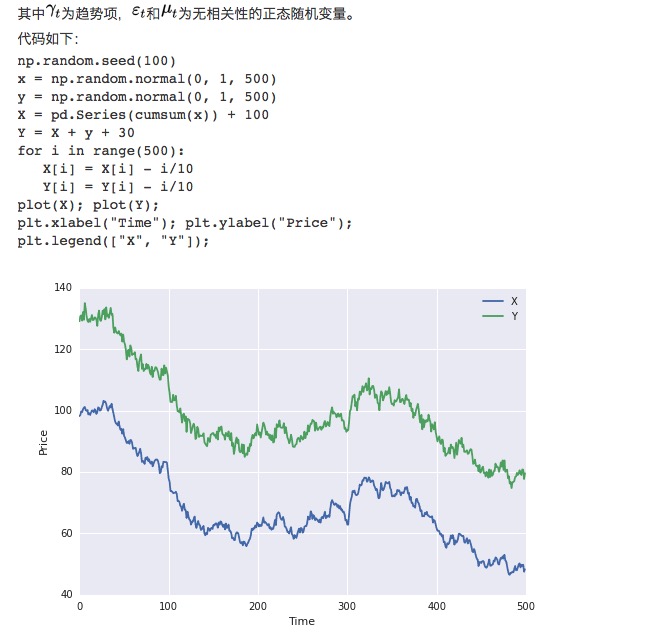
Offensichtlich sind die beiden Datensätze nicht gleichmäßig, da die Mittelwerte mit der Zeit variieren. Die beiden Datensätze sind jedoch in einer kohärenten Beziehung, da ihre Differenzreihen gleichmäßig sind:

plot(Y-X); plt.axhline((Y-X).mean(),color=“red”, linestyle=“–”); plt.xlabel(“Time”); plt.ylabel(“Price”); plt.legend([“Y-X”, “Mean”]);

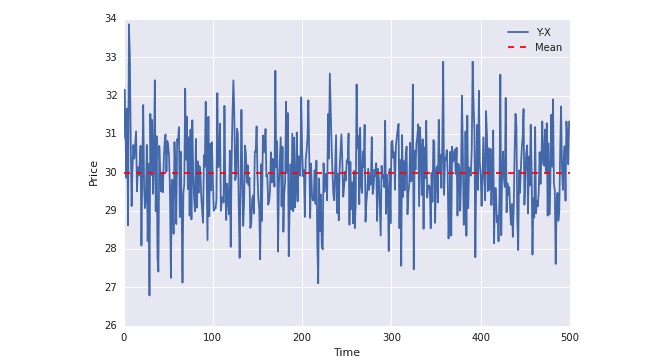
In der obigen Grafik kann man sehen, dass die blaue Linie immer um den Mittelwert schwankt. Der Mittelwert ändert sich nicht mit der Zeit.

• Zusammenfassung

Wenn man die Integration nur aus mathematischer Sicht erklärt, wird es komplizierter, was in einem späteren Quantitative-Unterricht zu berücksichtigen sein wird. Wir haben nur eine einfache Einführung auf der Ebene von Level 0 gemacht, um die Integration besser mit praktischen Anwendungen zu verbinden.

Ich habe mir das Bild von der Klassenaufnahme für die Quantifizierung von Fragen und Antworten geteilt.