Kurtosis und Schiefe

• #### Kurtosis und Skewness

Geschrieben von EasyTrader

Das ist eine Handelsstrategie, die von kurtosis und skewness angewendet wird. Wir handeln mehr, wenn die Daten tendenziell sind und die potenzielle Tendenz positiv ist. Wir handeln leer, wenn die Daten tendenziell sind und die potenzielle Tendenz negativ ist.

Wie können wir also Trends und die Stärke von Trends bestimmen?

Zunächst einmal die Definition einer normalen Verteilung.

Verteilung: Verteilung, bei der alle Werte in einer Variablen so häufig vorkommen, dass die Werte der Variablen in der Quer- und in der Vertikal-Achse dargestellt werden. Normale Verteilung: auch Gaussianische Verteilung genannt

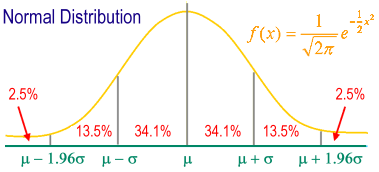
Standardnormale Verteilung: Eine Standardverteilung, in der der Mittelwert (mean) im Zentrum steht und die Standarddeviation (standard deviation) als die grundlegende Einheit der Achse der Kennziffer dargestellt wird. Symmetrische Grafik in der Form einer umgekehrten Glocke.

m ± 1s enthält 68,26% der gesamten Probengruppe.

m ± 2s enthält 95,44% der gesamten Probengruppe.

m ± 3s enthält 99,74% der gesamten Stichprobe.

95% der Fälle fallen zwischen m ± 1.96s.

99% der Individuen fallen zwischen m ± 2.58s.

In der Statistik misst die Spitze (Kurtosis) den Spitzenzustand der Wahrscheinlichkeitsverteilung einer realen Zufallsvariablen. Eine hohe Spitze bedeutet, dass die Differenz durch extreme Differenzen, die größer oder kleiner als der Durchschnitt sind, verursacht wird.

Kurtosis ist eine statistische Maßnahme, die den Grad der Schärfe der Verteilungsform eines Datensatzes beschreibt. Die Spitzen der normalen Verteilung sind 3, daher nennen wir Spitzen, die größer als 3 sind, um die Verteilung der Daten als normal zu beschreiben. Wir nennen Spitzen, die kleiner als 3 sind, flachspitze, um die Verteilung der Daten als positiv zu beschreiben.

Skewness beschreibt die Symmetrie der Verteilung der Daten, oder die Position des Modus der Zahl in den Daten. Eine Skewness von 0 ist eine perfekte Symmetrie. Diese Kennzahl wird auch mit einer normalen Verteilung verglichen: Eine Skewness größer als 0 zeigt, dass die Array rechts abweicht, als der lange Schwanz der rechten Seite und die äußersten Werte eher auf der rechten Seite angeordnet sind; im Gegensatz dazu ist eine Skewness der linken Seite, als der lange Schwanz der linken Seite und die äußersten Werte eher auf der linken Seite angeordnet sind. In den Finanzmärkten kann eine Skewness größer als 0 als eine Tendenz zur Neigung zur Sammlung von Daten interpretiert werden, während eine Skewness kleiner als 0 als eine Tendenz zur Neigung zur Sammlung von Daten interpretiert werden.

In der Wahrscheinlichkeitslehre und der Statistik misst die Ausrichtung die Asymmetrie der Wahrscheinlichkeitsverteilung einer realen Zufallsvariablen. Die Ausrichtung kann positiv, negativ oder gar nicht definiert sein. Quantitativ bedeutet eine negative Ausrichtung, dass die Spitze der Wahrscheinlichkeitsdichte-Funktion auf der linken Seite länger als auf der rechten ist, wobei die Mehrheit der Werte (einschließlich der Mittelzahl) auf der rechten Seite des Durchschnitts liegt.

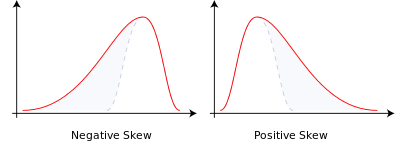
Es gibt zwei Arten von Verzerrungen:

• Negative oder linke Verzerrung: Die Linke hat einen längeren Schwanz und die verteilten Körper sind auf der rechten Seite konzentriert.
• Positiv- oder Rechtsparalytisch: Der rechts liegende Schwanz ist länger und der verteilte Körper ist auf der linken Seite konzentriert.
• Wenn die Verteilung symmetrisch ist, dann ist der Mittelwert = der Mittelwert und die Abweichung Null (zudem ist der Mittelwert = der Mittelwert = die Zahl).

• Der Grundsatz der Transaktionsregeln lautet: Wenn die Spitze kleiner als 0 ist (der Markt ist im Trendmarkt), ist die Verzerrung größer als N (der Trend ist aufwärts), und Sie tun mehr; Wenn die Spitze kleiner als 0 ist (der Markt ist im Trendmarkt), die Abweichung kleiner als M ist (der Trend ist rückläufig), wird der Shorting durchgeführt.

MATLAB-Quelle: Interessierte können sich für eine Testversion der Sprache JS anmelden.

input:ExitType(5) ;
input:NBarL(2),NBarS(2),TradeProfit(0.053),TradeStopLoss(0.023),ATRs_L(5.4),ATRs_S(10.9);
vars: IsBalanceDay(False),MP(0),PF(0),PL(0),HLRange(100);

inputs:Length(20),Trigger(3),UpSkew(3.4),DownSkew(2.2) ;
vars:KurtValue(0),SkewValue(0),BuyPoint(0),SellPoint(0);

MP = MarketPosition ;
if DAYofMonth(Date) > 14 and DAYofMonth(Date) < 22 and DAYofWeek(Date)= 3 then isBalanceDay = True else isBalanceDay =False ;

PF = AvgPrice*TradeProfit ;
PL = AvgPrice*TradeStopLoss ;

{计算峰度 }
KurtValue = Kurtosis(Close,Length) ;
{计算偏度}
SkewValue = Skew(Close,Length) ;

{ 峰度向下跌破 Trigger 线 ,建立买卖点 }
if KurtValue Cross under Trigger then Begin
BuyPoint = High 3;
SellPoint = Low-3;
end;

{ 偏度大于某数值后 ,趋势确认进场作多 }
if  SkewValue > -UpSkew 2 then Buy next bar at BuyPoint stop ;
{ 偏度小于某数值后 ,趋势确认进场作空 }
if  SkewValue < -DownSkew 2 then Sell next bar at SellPoint Stop ;
end;

if ExitType = 1 then SetStopLoss(PL * BigPointValue) ;

if ExitType = 2 then Begin
SetStopLoss(PL * BigPointValue) ;
setProfitTarget(PF * BigPointValue) ;
end;

if ExitType = 3 then Begin
if MP > 0 and BarsSinceEntry = NBarL then ExitLong next bar at Market ;
if MP < 0 and BarsSinceEntry = NBarS then ExitShort next bar at Market ;
end;

if ExitType = 4 then Begin
SetStopLoss(PL * BigPointValue) ;
setProfitTarget(PF * BigPointValue) ;
if MP > 0 and BarsSinceEntry = NBarL then {Sell } ExitLong next bar at Market ;
if MP < 0 and BarsSinceEntry = NBarS then {Buy} ExitShort next bar at Market ;
end;

if ExitType = 5 then Begin
{*******************************************************************
Description : ATR Trailing Stop Long Exit
Provided By : Omega Research, Inc. (c) Copyright 1999
********************************************************************}
{Inputs: ATRs_L(3);}
Variables: PosHigh(0), ATRVal_L(0);

ATRVal_L = AvgTrueRange(10) * ATRs_L;
If BarsSinceEntry = 0 Then PosHigh = High;
If MarketPosition = 1 Then Begin
If High > PosHigh Then PosHigh = High;
ExitLong ("ATR") Next Bar at PosHigh - ATRVal_L Stop;
End else ExitLong ("ATR eb") Next bar at High - ATRVal_L Stop;

{*******************************************************************
Description : ATR Trailing Stop Short Exit
Provided By : Omega Research, Inc. (c) Copyright 1999
******************************************************************}
{Inputs: ATRs_S(3);}
Variables: PosLow(0), ATRVal_S(0);

ATRVal_S = AvgTrueRange(10) * ATRs_S;
If BarsSinceEntry = 0 Then PosLow = Low;
If MarketPosition = -1 Then Begin
If Low < PosLow Then PosLow = Low;
ExitShort ("ATR_1") Next Bar at PosLow ATRVal_S Stop;
End else ExitShort ("ATR_1 eb") Next bar at Low ATRVal_S Stop;
end;

if IsBalanceDay then setExitonClose ;

Übertragung von Farutos Blog