Bayesianischer Klassifikator basierend auf dem KNN-Algorithmus

Theoretische Grundlagen für die Konzeption von Klassifikatoren für Klassifikationsentscheidungen:

Vergleichen Sie P ((ωi 173xxx) ⋅, wobeiωi der i-Klasse ist und x eine beobachtete und zu klassifizierende Datenmenge ist. P ((ωi 173xx) gibt an, wie hoch die Wahrscheinlichkeit ist, dass diese Datenmenge der i-Klasse angehört, wenn die Merkmale dieser Datenmenge bekannt sind, was auch die Nachprüfungswahrscheinlichkeit ist.

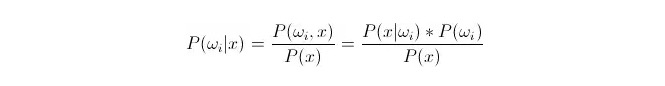
P (x) {\displaystyle P (x) } wird als Wahrscheinlichkeit der Ähnlichkeit oder der Klasseneignung bezeichnet. P (ω) {\displaystyle P (i) } wird als Vorherrschungswahrscheinlichkeit bezeichnet, da sie unabhängig vom Versuch ist und vor dem Versuch bekannt ist.

Bei der Klassifizierung ist die Kategorie zu wählen, in der die Nachprüfungswahrscheinlichkeit P ((ωiⴰⵙⴰⵙx) größer ist. Wenn P ((ωiⴰⵙx) unter jeder Kategorie klein ist, ist ωi variabel und x ist fest; so kann P ((x) entfernt und nicht berücksichtigt werden.

Und so kommt es darauf an, dass wir P (x) haben.*P ((ωi) Frage Die Vorauswahrscheinlichkeit P ((ωi) ist gut, wenn man nur den Anteil der Daten, die unter jeder Klassifizierung des statistischen Trainingszentrum erscheinen, berücksichtigt.

Die Wahrscheinlichkeit, dass P (x < i > i) ausgerechnet wird, ist unmöglich, da es sich um die Daten aus dem Testsatz handelt, die nicht direkt aus dem Trainingssatz abgeleitet werden können. Dann müssen wir die Verteilungsregeln der Trainingssatzdaten finden, um P (x < i > i) zu erhalten.

Im Folgenden werden die k-Nachbarschaftsalgorithmen (auf Englisch KNN) vorgestellt.

Wir wollen die Verteilung dieser Daten unter der Kategorie ωi anhand der Daten x1, x2…xn aus dem Trainingszentrum (wobei jedes der Daten m-dimensional ist). Angenommen, x ist ein beliebiger Punkt in m-dimensionalen Räumen, wie berechnet man P (x) undωi?

Wir wissen, dass man die Wahrscheinlichkeit mit einer proportionalen Annäherung berechnen kann, wenn die Datenmenge groß genug ist. Anhand dieses Prinzips kann man die nächsten k Stichprobenpunkte in der Umgebung des Punktes x finden, die der Kategorie i angehören. Berechnen Sie das Volumen V der kleinsten Supersphäre, die diese Stichprobenpunkte umschließt; und finden Sie heraus, wie viele der Stichprobendaten der Kategorie ωi angehören.

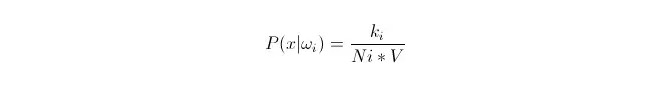
Wie wir sehen können, berechneten wir die Dichte der Klassengewohnheitswahrscheinlichkeit für den Punkt x.

Was ist mit P (ωi)? Nach der obigen Methode ist P ((ωi) = Ni/N 。 wobei N die Gesamtzahl der Proben 。 ist. Außerdem ist P (x) = k/N.*V), wobei k die Anzahl aller Stichprobenpunkte um den Supersphären ist; N die Gesamtzahl der Stichproben. Wenn wir das in die Formel einfügen, können wir leicht herausfinden:

P(ωi|x)=ki/k

In einer Supersphäre der Größe V umgeben sich k Proben, von denen einige der Kategorie i angehören. Auf diese Weise können wir bestimmen, welcher Typ von Proben am meisten umgeben ist und welcher Kategorie x angehören sollte. Dies ist der Klassifikator, der mit der k-nahen Algorithmus entwickelt wurde.