Überlegungen zu Hochfrequenzhandelsstrategien (2)
 1
1
 3416
3416
Der Artikel befasst sich hauptsächlich mit Hochfrequenzhandelsstrategien und konzentriert sich auf die Modellierung kumulativer Mengen und Preisschocks. In diesem Dokument wird ein vorläufiges Modell zur optimalen Auftragserteilung vorgeschlagen, indem die Auswirkungen einzelner Transaktionen, Preisschocks mit festen Intervallen und des Transaktionsvolumens auf die Preise analysiert werden. Dieses Modell versucht, die optimale Handelsposition basierend auf dem Verständnis von Volumen- und Preisschocks zu finden. Die Annahmen des Modells werden ausführlich erörtert und durch einen Vergleich der tatsächlichen und der vom Modell prognostizierten erwarteten Rendite wird eine vorläufige Einschätzung der optimalen Auftragserteilung vorgenommen.
Kumulative Volumenmodellierung
Im vorherigen Artikel wurde der Wahrscheinlichkeitsausdruck dafür abgeleitet, dass ein einzelnes Transaktionsvolumen einen bestimmten Wert überschreitet:
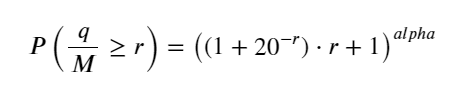
Wir sind auch an der Verteilung des Handelsvolumens über einen bestimmten Zeitraum interessiert, die intuitiv mit dem Volumen jeder einzelnen Transaktion und der Auftragshäufigkeit in Zusammenhang stehen sollte. Anschließend werden die Daten in festgelegten Zeitabständen verarbeitet. Stellen Sie die Verteilung wie oben dargestellt dar.
from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
trades = pd.read_csv('HOOKUSDT-aggTrades-2023-01-27.csv')
trades['date'] = pd.to_datetime(trades['transact_time'], unit='ms')
trades.index = trades['date']
buy_trades = trades[trades['is_buyer_maker']==False].copy()
buy_trades = buy_trades.groupby('transact_time').agg({
'agg_trade_id': 'last',
'price': 'last',
'quantity': 'sum',
'first_trade_id': 'first',
'last_trade_id': 'last',
'is_buyer_maker': 'last',
'date': 'last',
'transact_time':'last'
})
buy_trades['interval']=buy_trades['transact_time'] - buy_trades['transact_time'].shift()
buy_trades.index = buy_trades['date']
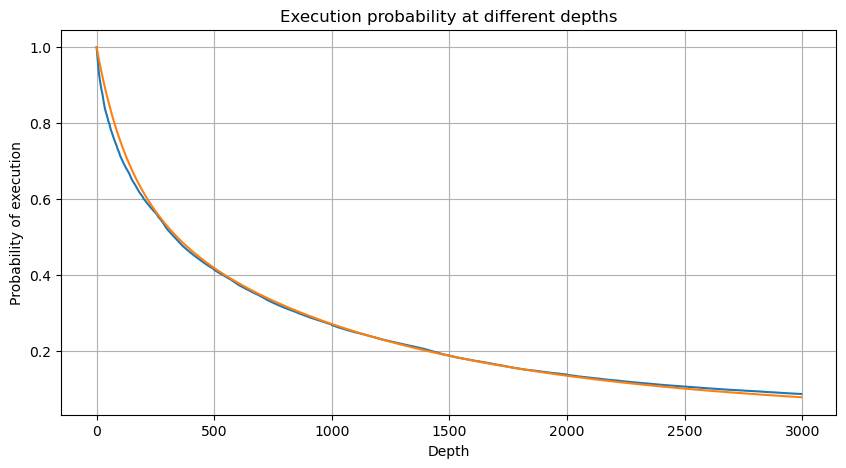
Führen Sie das Transaktionsvolumen alle 1s zusammen, entfernen Sie den Teil, in dem keine Transaktion stattgefunden hat, und verwenden Sie die obige Verteilung einzelner Transaktionen zur Anpassung. Es ist ersichtlich, dass das Ergebnis besser ist. Wenn alle Transaktionen innerhalb von 1s als einzelne Transaktionen betrachtet werden, wird dieses Problem Das Problem ist inzwischen gelöst. Wird der Zyklus jedoch verlängert (im Verhältnis zur Transaktionshäufigkeit), so stellt man fest, dass der Fehler zunimmt. Untersuchungen haben ergeben, dass dieser Fehler durch den vorherigen Korrekturterm der Pareto-Verteilung verursacht wird. Dies bedeutet, dass sich die Kombination mehrerer Transaktionen der Pareto-Verteilung annähert, wenn der Zyklus länger wird und mehr Einzeltransaktionen umfasst. In diesem Fall sollte der Korrekturterm entfernt werden.
df_resampled = buy_trades['quantity'].resample('1S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]
buy_trades
| agg_trade_id | price | quantity | first_trade_id | last_trade_id | is_buyer_maker | date | transact_time | interval | diff | |
|---|---|---|---|---|---|---|---|---|---|---|
| 2023-01-27 00:00:00.161 | 1138369 | 2.901 | 54.3 | 3806199 | 3806201 | False | 2023-01-27 00:00:00.161 | 1674777600161 | NaN | 0.001 |
| 2023-01-27 00:00:04.140 | 1138370 | 2.901 | 291.3 | 3806202 | 3806203 | False | 2023-01-27 00:00:04.140 | 1674777604140 | 3979.0 | 0.000 |
| 2023-01-27 00:00:04.339 | 1138373 | 2.902 | 55.1 | 3806205 | 3806207 | False | 2023-01-27 00:00:04.339 | 1674777604339 | 199.0 | 0.001 |
| 2023-01-27 00:00:04.772 | 1138374 | 2.902 | 1032.7 | 3806208 | 3806223 | False | 2023-01-27 00:00:04.772 | 1674777604772 | 433.0 | 0.000 |
| 2023-01-27 00:00:05.562 | 1138375 | 2.901 | 3.5 | 3806224 | 3806224 | False | 2023-01-27 00:00:05.562 | 1674777605562 | 790.0 | 0.000 |
| … | … | … | … | … | … | … | … | … | … | … |
| 2023-01-27 23:59:57.739 | 1544370 | 3.572 | 394.8 | 5074645 | 5074651 | False | 2023-01-27 23:59:57.739 | 1674863997739 | 1224.0 | 0.002 |
| 2023-01-27 23:59:57.902 | 1544372 | 3.573 | 177.6 | 5074652 | 5074655 | False | 2023-01-27 23:59:57.902 | 1674863997902 | 163.0 | 0.001 |
| 2023-01-27 23:59:58.107 | 1544373 | 3.573 | 139.8 | 5074656 | 5074656 | False | 2023-01-27 23:59:58.107 | 1674863998107 | 205.0 | 0.000 |
| 2023-01-27 23:59:58.302 | 1544374 | 3.573 | 60.5 | 5074657 | 5074657 | False | 2023-01-27 23:59:58.302 | 1674863998302 | 195.0 | 0.000 |
| 2023-01-27 23:59:59.894 | 1544376 | 3.571 | 12.1 | 5074662 | 5074664 | False | 2023-01-27 23:59:59.894 | 1674863999894 | 1592.0 | 0.000 |
#1s内的累计分布
depths = np.array(range(0, 3000, 5))
probabilities = np.array([np.mean(df_resampled['quantity'] > depth) for depth in depths])
mean = df_resampled['quantity'].mean()
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2.05)
probabilities_s = np.array([((1+20**(-depth/mean))*depth/mean+1)**(alpha) for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities)
plt.plot(depths, probabilities_s)
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.grid(True)
df_resampled = buy_trades['quantity'].resample('30S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]
depths = np.array(range(0, 12000, 20))
probabilities = np.array([np.mean(df_resampled['quantity'] > depth) for depth in depths])
mean = df_resampled['quantity'].mean()
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2.05)
probabilities_s = np.array([((1+20**(-depth/mean))*depth/mean+1)**(alpha) for depth in depths])
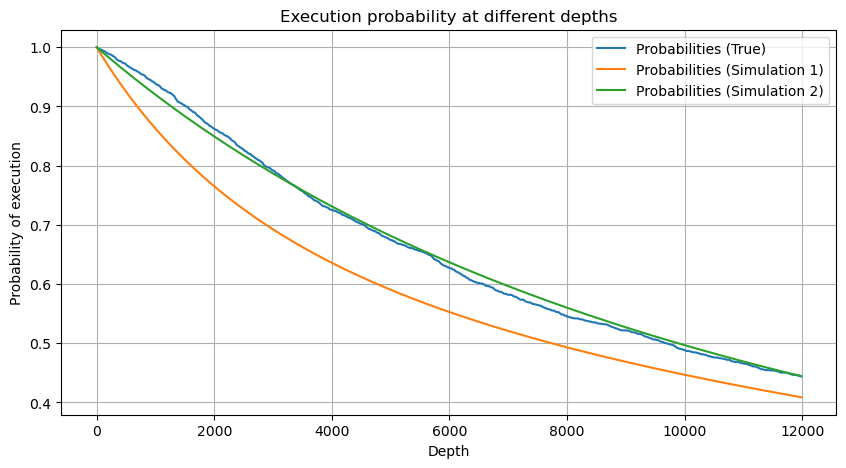
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2)
probabilities_s_2 = np.array([(depth/mean+1)**alpha for depth in depths]) # 无修正
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities,label='Probabilities (True)')
plt.plot(depths, probabilities_s, label='Probabilities (Simulation 1)')
plt.plot(depths, probabilities_s_2, label='Probabilities (Simulation 2)')
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.legend()
plt.grid(True)
Nun haben wir eine allgemeine Formel für die Verteilung des kumulierten Handelsvolumens zu verschiedenen Zeitpunkten zusammengefasst und die Verteilung einzelner Transaktionen verwendet, um diese anzupassen, ohne sie jedes Mal separat zählen zu müssen. Hier lassen wir den Vorgang aus und geben die Formel direkt an:
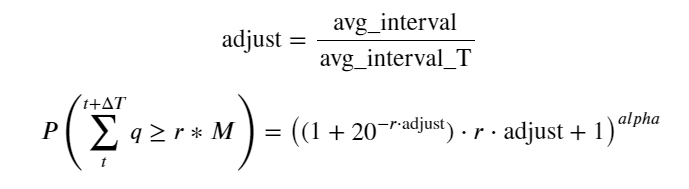
Unter diesen stellt avg_interval das durchschnittliche Intervall zwischen einzelnen Transaktionen dar und avg_interval_T stellt das durchschnittliche Intervall der Intervalle dar, die geschätzt werden müssen. Das ist etwas verwirrend. Wenn wir die Transaktionszeit von 1 Sekunde schätzen möchten, müssen wir das durchschnittliche Intervall zwischen Ereignissen berechnen, die Transaktionen innerhalb von 1 Sekunde enthalten. Wenn die Wahrscheinlichkeit des Eintreffens einer Bestellung der Poisson-Verteilung entspricht, sollte es möglich sein, sie hier direkt abzuschätzen. Die tatsächliche Abweichung ist jedoch groß, sodass wir sie hier nicht erläutern.
Beachten Sie, dass die Wahrscheinlichkeit, dass das Volumen innerhalb eines bestimmten Intervalls größer als ein bestimmter Wert ist, sich deutlich von der tatsächlichen Wahrscheinlichkeit der Transaktion an dieser Position in der Tiefe unterscheiden sollte, denn je länger die Wartezeit ist, desto größer ist die Möglichkeit des Auftragsbuchs Änderungen, und die Transaktion führt auch zu Änderungen der Tiefe, sodass sich die Transaktionswahrscheinlichkeit an derselben Tiefenposition in Echtzeit ändert, wenn die Daten aktualisiert werden.
df_resampled = buy_trades['quantity'].resample('2S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]
depths = np.array(range(0, 6500, 10))
probabilities = np.array([np.mean(df_resampled['quantity'] > depth) for depth in depths])
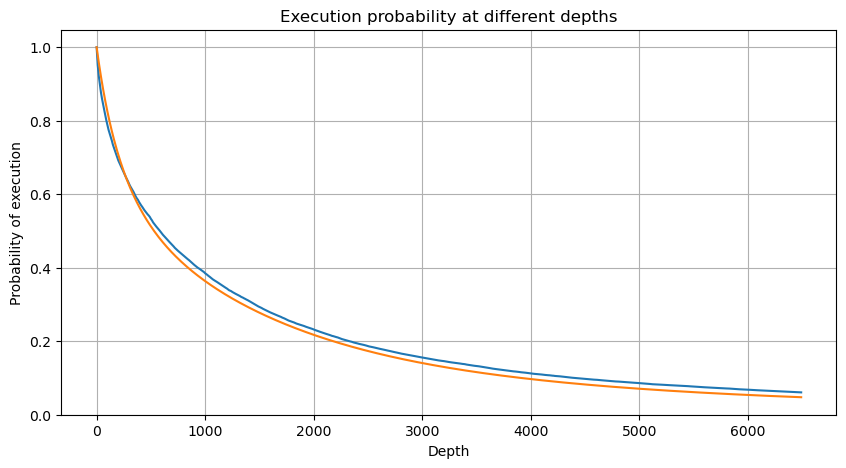
mean = buy_trades['quantity'].mean()
adjust = buy_trades['interval'].mean() / 2620
alpha = np.log(np.mean(buy_trades['quantity'] > mean))/0.7178397931503168
probabilities_s = np.array([((1+20**(-depth*adjust/mean))*depth*adjust/mean+1)**(alpha) for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities)
plt.plot(depths, probabilities_s)
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.grid(True)
Auswirkungen auf den Preis einer einzelnen Transaktion
Transaktionsdaten sind ein Schatz, und es können noch immer viele Daten daraus gewonnen werden. Wir sollten den Einfluss von Aufträgen auf die Preise genau beachten, da dieser Einfluss auf die Platzierung ausstehender Aufträge in der Strategie hat. Berechnen Sie auf ähnliche Weise basierend auf den aggregierten Daten von transact_time die Differenz zwischen dem letzten und dem ersten Preis. Wenn nur eine Bestellung vorliegt, beträgt die Differenz 0. Das Merkwürdige ist, dass es immer noch eine kleine Anzahl von Datenergebnissen mit negativen Ergebnissen gibt. Dies dürfte ein Problem mit der Reihenfolge der Datenanordnung sein, daher werde ich hier nicht näher darauf eingehen.
Die Ergebnisse zeigen, dass der Anteil ohne Auswirkung 77 % beträgt, der Anteil von 1 Tick 16,5 %, von 2 Ticks 3,7 %, von 3 Ticks 1,2 % und der Anteil von mehr als 4 Ticks weniger als 1 % beträgt. . Dies entspricht grundsätzlich den Eigenschaften der Exponentialfunktion, die Anpassung ist jedoch nicht genau.
Das Transaktionsvolumen, das den entsprechenden Preisunterschied verursacht hat, wurde gezählt und die durch einen zu großen Einfluss verursachte Verzerrung wurde entfernt. Es entspricht grundsätzlich der linearen Beziehung, und etwa jedes 1.000 Volumen verursacht eine Preisschwankung von 1 Tick. Man kann auch davon ausgehen, dass die durchschnittliche Anzahl ausstehender Aufträge bei jedem Preis etwa 1.000 beträgt.
diff_df = trades[trades['is_buyer_maker']==False].groupby('transact_time')['price'].agg(lambda x: abs(round(x.iloc[-1] - x.iloc[0],3)) if len(x) > 1 else 0)
buy_trades['diff'] = buy_trades['transact_time'].map(diff_df)
diff_counts = buy_trades['diff'].value_counts()
diff_counts[diff_counts>10]/diff_counts.sum()
0.000 0.769965
0.001 0.165527
0.002 0.037826
0.003 0.012546
0.004 0.005986
0.005 0.003173
0.006 0.001964
0.007 0.001036
0.008 0.000795
0.009 0.000474
0.010 0.000227
0.011 0.000187
0.012 0.000087
0.013 0.000080
Name: diff, dtype: float64
diff_group = buy_trades.groupby('diff').agg({
'quantity': 'mean',
'diff': 'last',
})
diff_group['quantity'][diff_group['diff']>0][diff_group['diff']<0.01].plot(figsize=(10,5),grid=True);
Preisschocks in regelmäßigen Abständen
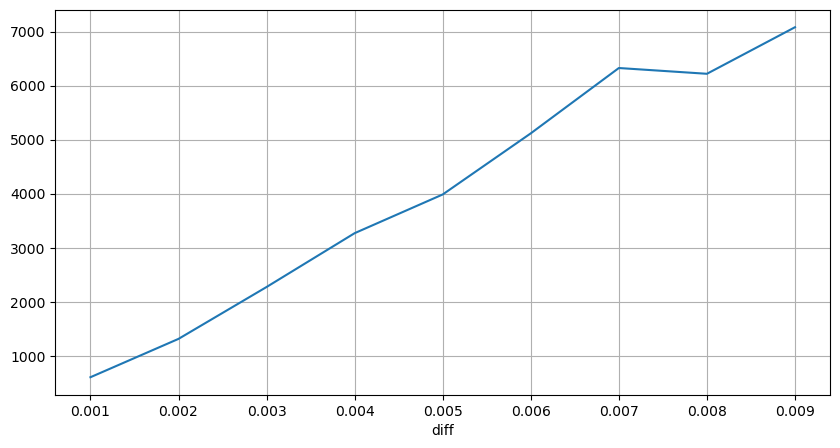
Zählen Sie die Preisauswirkungen innerhalb von 2 Sekunden. Der Unterschied besteht darin, dass es negative Werte geben wird. Da hier nur Kaufaufträge gezählt werden, ist die symmetrische Position natürlich einen Tick größer. Beobachten Sie weiterhin die Beziehung zwischen Handelsvolumen und Auswirkung und zählen Sie nur die Ergebnisse, die größer als 0 sind. Die Schlussfolgerung ähnelt der einer einzelnen Order, bei der es sich ebenfalls um eine annähernd lineare Beziehung handelt. Für jeden Tick sind etwa 2000 Volumen erforderlich.
df_resampled = buy_trades.resample('2S').agg({
'price': ['first', 'last', 'count'],
'quantity': 'sum'
})
df_resampled['price_diff'] = round(df_resampled[('price', 'last')] - df_resampled[('price', 'first')],3)
df_resampled['price_diff'] = df_resampled['price_diff'].fillna(0)
result_df_raw = pd.DataFrame({
'price_diff': df_resampled['price_diff'],
'quantity_sum': df_resampled[('quantity', 'sum')],
'data_count': df_resampled[('price', 'count')]
})
result_df = result_df_raw[result_df_raw['price_diff'] != 0]
result_df['price_diff'][abs(result_df['price_diff'])<0.016].value_counts().sort_index().plot.bar(figsize=(10,5));
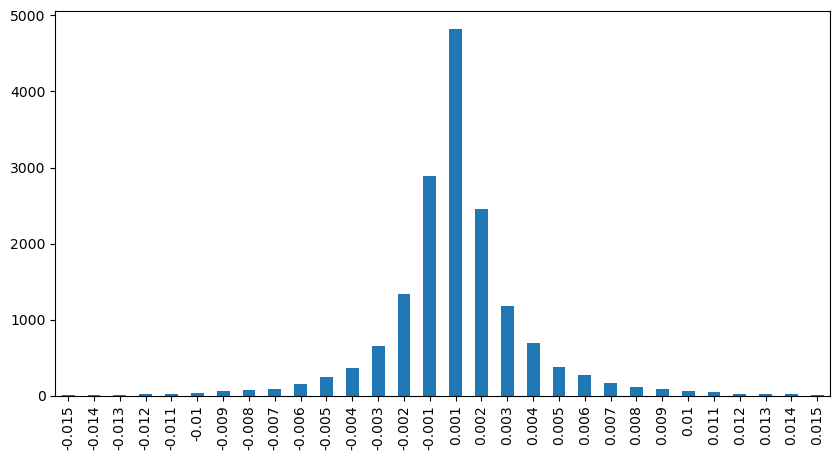
result_df['price_diff'].value_counts()[result_df['price_diff'].value_counts()>30]
0.001 7176
-0.001 3665
0.002 3069
-0.002 1536
0.003 1260
0.004 692
-0.003 608
0.005 391
-0.004 322
0.006 259
-0.005 192
0.007 146
-0.006 112
0.008 82
0.009 75
-0.007 75
-0.008 65
0.010 51
0.011 41
-0.010 31
Name: price_diff, dtype: int64
diff_group = result_df.groupby('price_diff').agg({ 'quantity_sum': 'mean'})
diff_group[(diff_group.index>0) & (diff_group.index<0.015)].plot(figsize=(10,5),grid=True);
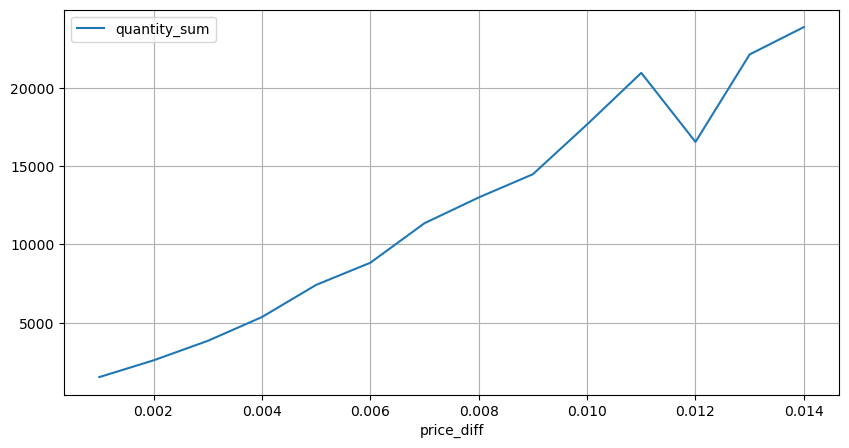
Preisauswirkungen des Volumens
Das für eine Tick-Änderung erforderliche Volumen wurde bereits früher berechnet, ist jedoch nicht genau, da es auf der Annahme basiert, dass die Auswirkung bereits eingetreten ist. Betrachten wir nun die Preisauswirkungen des Handelsvolumens.
Die Daten werden hier im Sekundentakt abgetastet, wobei 100 Mengen einen Schritt darstellen, und die Preisänderungen innerhalb dieses Mengenbereichs werden gezählt. Es wurden einige wertvolle Schlussfolgerungen gezogen:
- Wenn das Kaufvolumen unter 500 liegt, ist die erwartete Preisänderung nach unten, was zu erwarten ist, da auch Verkaufsaufträge vorliegen, die den Preis beeinflussen.
- Bei geringem Handelsvolumen folgt es einer linearen Beziehung, das heißt, je größer das Handelsvolumen, desto größer der Preisanstieg.
- Je größer das Volumen der Kaufaufträge, desto größer die Preisänderung, die häufig einen Preisdurchbruch darstellt. Nach dem Durchbruch kann der Preis zurückkehren. In Verbindung mit der Stichprobennahme in festen Intervallen sind die Daten instabil.
- Aufmerksamkeit sollte dem oberen Teil des Streudiagramms gewidmet werden, also dem Teil, in dem das Volumen der Preissteigerung entspricht.
- Nur für dieses Handelspaar wird eine grobe Version der Beziehung zwischen Volumen und Preisänderung angegeben:
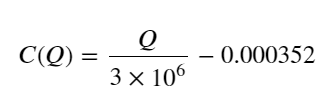
Dabei steht „C“ für die Preisänderung und „Q“ für das Kaufauftragsvolumen.
df_resampled = buy_trades.resample('1S').agg({
'price': ['first', 'last', 'count'],
'quantity': 'sum'
})
df_resampled['price_diff'] = round(df_resampled[('price', 'last')] - df_resampled[('price', 'first')],3)
df_resampled['price_diff'] = df_resampled['price_diff'].fillna(0)
result_df_raw = pd.DataFrame({
'price_diff': df_resampled['price_diff'],
'quantity_sum': df_resampled[('quantity', 'sum')],
'data_count': df_resampled[('price', 'count')]
})
result_df = result_df_raw[result_df_raw['price_diff'] != 0]
df = result_df.copy()
bins = np.arange(0, 30000, 100) #
labels = [f'{i}-{i+100-1}' for i in bins[:-1]]
df.loc[:, 'quantity_group'] = pd.cut(df['quantity_sum'], bins=bins, labels=labels)
grouped = df.groupby('quantity_group')['price_diff'].mean()
grouped_df = pd.DataFrame(grouped).reset_index()
grouped_df['quantity_group_center'] = grouped_df['quantity_group'].apply(lambda x: (float(x.split('-')[0]) + float(x.split('-')[1])) / 2)
plt.figure(figsize=(10,5))
plt.scatter(grouped_df['quantity_group_center'], grouped_df['price_diff'],s=10)
plt.plot(grouped_df['quantity_group_center'], np.array(grouped_df['quantity_group_center'].values)/2e6-0.000352,color='red')
plt.xlabel('quantity_group_center')
plt.ylabel('average price_diff')
plt.title('Scatter plot of average price_diff by quantity_group')
plt.grid(True)
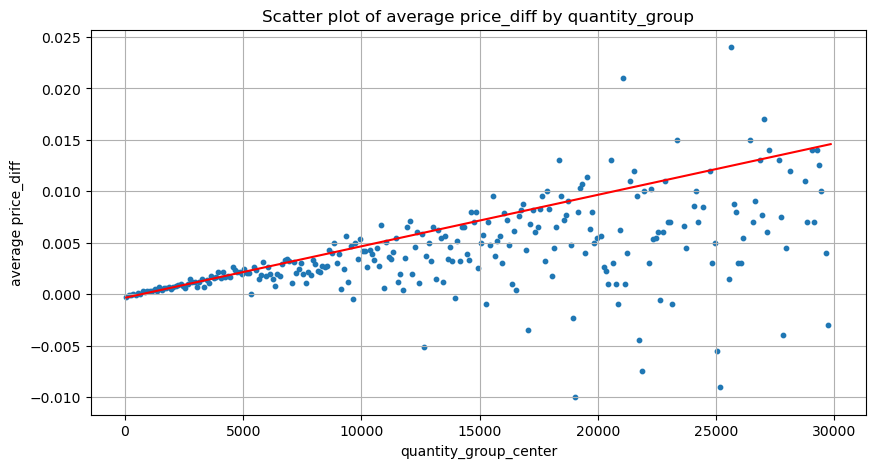
grouped_df.head(10)
| quantity_group | price_diff | quantity_group_center | |
|---|---|---|---|
| 0 | 0-199 | -0.000302 | 99.5 |
| 1 | 100-299 | -0.000124 | 199.5 |
| 2 | 200-399 | -0.000068 | 299.5 |
| 3 | 300-499 | -0.000017 | 399.5 |
| 4 | 400-599 | -0.000048 | 499.5 |
| 5 | 500-699 | 0.000098 | 599.5 |
| 6 | 600-799 | 0.000006 | 699.5 |
| 7 | 700-899 | 0.000261 | 799.5 |
| 8 | 800-999 | 0.000186 | 899.5 |
| 9 | 900-1099 | 0.000299 | 999.5 |
Anfängliche optimale Auftragsposition
Mit der Modellierung des Handelsvolumens und einem groben Modell des Handelsvolumens entsprechend dem Preiseinfluss lässt sich anscheinend die optimale Auftragsposition berechnen. Lassen Sie uns einige Annahmen treffen und eine unverantwortliche optimale Preisposition angeben.
- Gehen Sie davon aus, dass der Preis nach dem Schock auf seinen ursprünglichen Wert zurückkehrt (das ist natürlich unwahrscheinlich und erfordert eine erneute Analyse der Preisänderungen nach dem Schock).
- Nehmen wir an, dass die Verteilung des Handelsvolumens und der Auftragshäufigkeit während dieses Zeitraums den voreingestellten Anforderungen entspricht (auch dies ist ungenau, da zur Schätzung der Wert eines Tages verwendet wird und die Transaktionen eine offensichtliche Häufung aufweisen).
- Nehmen wir an, dass während der Simulationszeit nur ein Verkaufsauftrag erfolgt und die Position dann geschlossen wird.
- Angenommen, es gibt nach der Auftragsausführung weitere Kaufaufträge, die den Preis weiter nach oben treiben, insbesondere wenn das Volumen sehr gering ist. Dieser Effekt wird hier ignoriert und es wird einfach davon ausgegangen, dass er wieder auftritt.
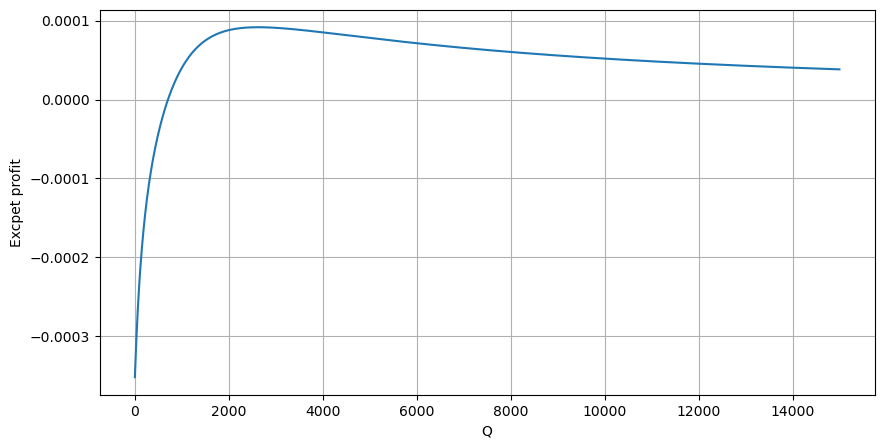
Schreiben Sie zunächst eine einfache erwartete Rendite auf, d. h. die Wahrscheinlichkeit, dass die kumulierte Kauforder innerhalb einer Sekunde größer als Q ist, multipliziert mit der erwarteten Rendite (d. h. dem Impact Price):
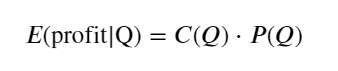
Die zu erwartende Rendite liegt laut Grafik bei rund 2500 maximal, was etwa dem 2,5-fachen des durchschnittlichen Handelsvolumens entspricht. Das heißt, die Verkaufsorder sollte bei 2500 platziert werden. Es muss noch einmal betont werden, dass die horizontale Achse das Handelsvolumen innerhalb von 1 Sekunde darstellt und nicht einfach mit der Tiefenposition gleichgesetzt werden kann. Und dies zu einem Zeitpunkt, an dem es noch an sehr wichtigen, detaillierten Daten mangelt und die Daten lediglich auf handelsbasierten Spekulationen basieren.
Zusammenfassen
Es zeigt sich, dass die Volumenverteilung in verschiedenen Zeitintervallen eine einfache Skalierung der Volumenverteilung einer einzelnen Transaktion ist. Wir haben auch ein einfaches Modell der erwarteten Rendite erstellt, das auf Preisschocks und Transaktionswahrscheinlichkeiten basiert. Die Ergebnisse dieses Modells entsprechen unseren Erwartungen. Wenn das Verkaufsauftragsvolumen gering ist, deutet dies auf einen Preisrückgang hin. Ein bestimmtes Volumen ist erforderlich, um haben Gewinnspannen, und je größer das Transaktionsvolumen, desto höher die Gewinnspanne. Je größer die Wahrscheinlichkeit, desto geringer ist sie. In der Mitte gibt es eine optimale Größe, die auch die Auftragsplatzierungsposition ist, nach der die Strategie sucht. Natürlich ist dieses Modell immer noch zu einfach. Im nächsten Artikel werde ich ausführlicher darauf eingehen.
#1s内的累计分布
df_resampled = buy_trades['quantity'].resample('1S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]
depths = np.array(range(0, 15000, 10))
mean = df_resampled['quantity'].mean()
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2.05)
probabilities_s = np.array([((1+20**(-depth/mean))*depth/mean+1)**(alpha) for depth in depths])
profit_s = np.array([depth/2e6-0.000352 for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities_s*profit_s)
plt.xlabel('Q')
plt.ylabel('Excpet profit')
plt.grid(True)