Der vorherige Artikel gab eine vorläufige Einführung in die Berechnungsmethoden verschiedener Mittelpreise und gab eine Wiederholung des Mittelpreises. Dieser Artikel befasst sich weiter mit diesem Thema.

Erforderliche Daten

Die Auftragsflussdaten und zehn Ebenen von Tiefendaten werden aus dem realen Handel gesammelt und die Aktualisierungsfrequenz beträgt 100 ms. Der reale Markt enthält lediglich die in Echtzeit aktualisierten Kauf- und Verkaufsdaten. Der Einfachheit halber wird er vorerst nicht verwendet. Da die Daten zu umfangreich sind, werden nur 100.000 Zeilen mit detaillierten Daten beibehalten und die Marktbedingungen für jede Ebene werden außerdem in separate Spalten unterteilt.

from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import ast
%matplotlib inline

tick_size = 0.0001

trades = pd.read_csv('YGGUSDT_aggTrade.csv',names=['type','event_time', 'agg_trade_id','symbol', 'price', 'quantity', 'first_trade_id', 'last_trade_id',
       'transact_time', 'is_buyer_maker'])

trades = trades.groupby(['transact_time','is_buyer_maker']).agg({
    'transact_time':'last',
    'agg_trade_id': 'last',
    'price': 'first',
    'quantity': 'sum',
    'first_trade_id': 'first',
    'last_trade_id': 'last',
    'is_buyer_maker': 'last',
})

trades.index = pd.to_datetime(trades['transact_time'], unit='ms')
trades.index.rename('time', inplace=True)
trades['interval'] = trades['transact_time'] - trades['transact_time'].shift()

depths = pd.read_csv('YGGUSDT_depth.csv',names=['type','event_time', 'transact_time','symbol', 'u1', 'u2', 'u3', 'bids','asks'])

depths = depths.iloc[:100000]

depths['bids'] = depths['bids'].apply(ast.literal_eval).copy()
depths['asks'] = depths['asks'].apply(ast.literal_eval).copy()

def expand_bid(bid_data):
    expanded = {}
    for j, (price, quantity) in enumerate(bid_data):
        expanded[f'bid_{j}_price'] = float(price)
        expanded[f'bid_{j}_quantity'] = float(quantity)
    return pd.Series(expanded)
def expand_ask(ask_data):
    expanded = {}
    for j, (price, quantity) in enumerate(ask_data):
        expanded[f'ask_{j}_price'] = float(price)
        expanded[f'ask_{j}_quantity'] = float(quantity)
    return pd.Series(expanded)
# 应用到每一行，得到新的df
expanded_df_bid = depths['bids'].apply(expand_bid)
expanded_df_ask = depths['asks'].apply(expand_ask)
# 在原有df上进行扩展
depths = pd.concat([depths, expanded_df_bid, expanded_df_ask], axis=1)

depths.index = pd.to_datetime(depths['transact_time'], unit='ms')
depths.index.rename('time', inplace=True);

trades = trades[trades['transact_time'] < depths['transact_time'].iloc[-1]]

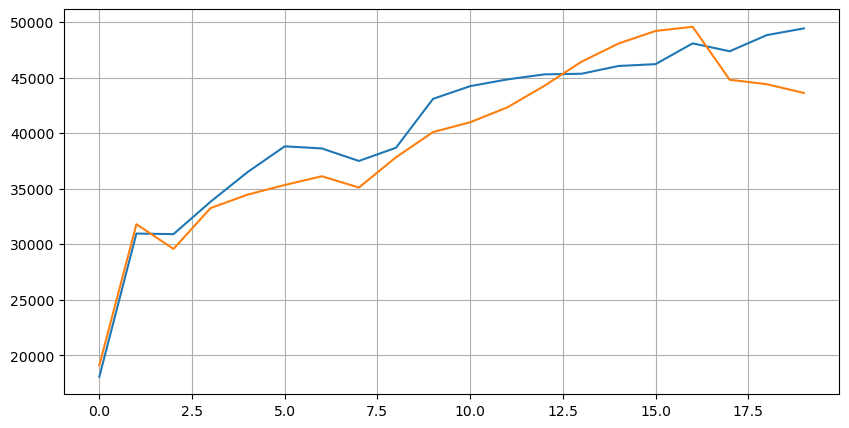
Schauen wir uns zunächst die Verteilung dieser 20 Marktbedingungen an. Sie entspricht den Erwartungen. Je weiter die Markteröffnung entfernt ist, desto mehr schwebende Aufträge gibt es, und die Kauf- und Verkaufsaufträge sind ungefähr symmetrisch.

bid_mean_list = []
ask_mean_list = []
for i in range(20):
    bid_mean_list.append(round(depths[f'bid_{i}_quantity'].mean(),0))
    ask_mean_list.append(round(depths[f'ask_{i}_quantity'].mean(),0))
plt.figure(figsize=(10, 5))
plt.plot(bid_mean_list);
plt.plot(ask_mean_list);
plt.grid(True)

Kombinieren Sie Tiefendaten und Transaktionsdaten, um die Bewertung der Prognosegenauigkeit zu erleichtern. Hier stellen wir sicher, dass die Transaktionsdaten alle später als die Tiefendaten sind. Ohne die Verzögerung zu berücksichtigen, berechnen wir direkt den mittleren quadratischen Fehler zwischen dem vorhergesagten Wert und dem tatsächlichen Transaktionspreis. Wird verwendet, um die Genauigkeit von Vorhersagen zu messen.

Den Ergebnissen zufolge ist der Fehler bei mid_price, dem Durchschnitt des Kauf-Verkaufs-Paares, am größten. Nach der Änderung von weight_mid_price wird der Fehler sofort viel kleiner und durch die Anpassung des gewichteten Mittelpreises wird er weiter verbessert. Nach der Veröffentlichung des gestrigen Artikels berichteten einige Leute, dass sie nur I^³⁄₂ verwendet hätten. Ich habe es hier überprüft und festgestellt, dass das Ergebnis besser war. Nach Überlegung des Grundes sollte es der Unterschied in der Häufigkeit der Ereignisse sein. Wenn I nahe bei -1 und 1 liegt, handelt es sich um ein Ereignis mit geringer Wahrscheinlichkeit. Um diese geringen Wahrscheinlichkeiten zu korrigieren, muss die Vorhersage von Ereignissen mit hoher Häufigkeit ist nicht so genau. Um mehr über hochfrequente Ereignisse zu erfahren, habe ich einige Anpassungen vorgenommen (dies sind rein experimentelle Parameter und für den tatsächlichen Handel nicht sehr nützlich):

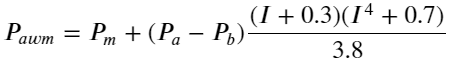
Das Ergebnis war etwas besser. Wie im vorherigen Artikel erwähnt, sollten Strategien mit mehr Daten vorhergesagt werden. Mit mehr Tiefe und Auftragserfüllungsdaten ist die Verbesserung, die durch die Verflechtung mit dem Marktpreis erzielt werden kann, bereits sehr schwach.

df = pd.merge_asof(trades, depths, on='transact_time', direction='backward')

df['spread'] = round(df['ask_0_price'] - df['bid_0_price'],4)
df['mid_price'] = (df['bid_0_price']+ df['ask_0_price']) / 2
df['I'] = (df['bid_0_quantity'] - df['ask_0_quantity']) / (df['bid_0_quantity'] + df['ask_0_quantity'])
df['weight_mid_price'] = df['mid_price'] + df['spread']*df['I']/2
df['adjust_mid_price'] = df['mid_price'] + df['spread']*(df['I'])*(df['I']**8+1)/4
df['adjust_mid_price_2'] = df['mid_price'] + df['spread']*df['I']*(df['I']**2+1)/4
df['adjust_mid_price_3'] = df['mid_price'] + df['spread']*df['I']**3/2
df['adjust_mid_price_4'] = df['mid_price'] + df['spread']*(df['I']+0.3)*(df['I']**4+0.7)/3.8

print('平均值     mid_price的误差：', ((df['price']-df['mid_price'])**2).sum())
print('挂单量加权 mid_price的误差：', ((df['price']-df['weight_mid_price'])**2).sum())
print('调整后的   mid_price的误差：', ((df['price']-df['adjust_mid_price'])**2).sum())
print('调整后的 mid_price_2的误差：', ((df['price']-df['adjust_mid_price_2'])**2).sum())
print('调整后的 mid_price_3的误差：', ((df['price']-df['adjust_mid_price_3'])**2).sum())
print('调整后的 mid_price_4的误差：', ((df['price']-df['adjust_mid_price_4'])**2).sum())

平均值     mid_price的误差： 0.0048751924999999845
挂单量加权 mid_price的误差： 0.0048373440193987035
调整后的   mid_price的误差： 0.004803654771638586
调整后的 mid_price_2的误差： 0.004808216498329721
调整后的 mid_price_3的误差： 0.004794984755260528
调整后的 mid_price_4的误差： 0.0047909595497071375

Berücksichtigen Sie die Tiefe des zweiten Gangs

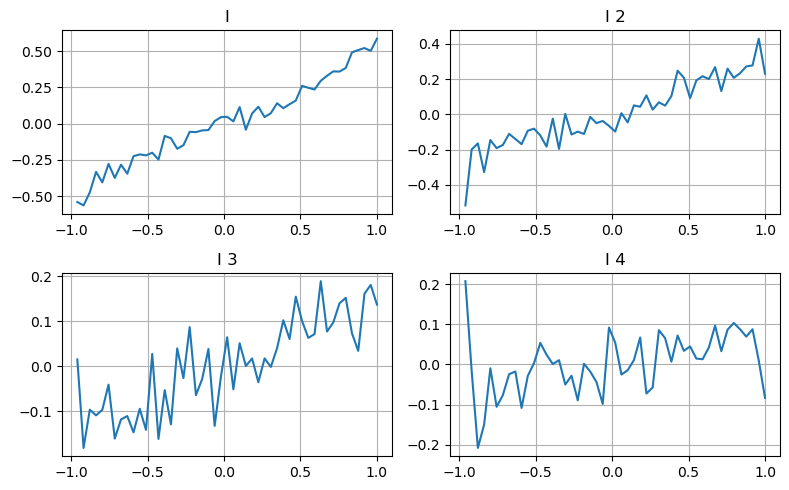
Hier verwenden wir die Idee des vorherigen Artikels, die verschiedenen Wertebereiche eines bestimmten Einflussparameters und die Änderungen des Transaktionspreises zu untersuchen, um den Beitrag dieses Parameters zum Mittelpreis zu messen. Wie im Tiefendiagramm der ersten Ebene gezeigt, ist es mit steigendem I wahrscheinlicher, dass sich der Preis der nächsten Transaktion positiv ändert, was bedeutet, dass I einen positiven Beitrag leistet.

Die zweite Partie wurde auf die gleiche Weise verarbeitet und es zeigte sich, dass der Effekt zwar etwas geringer war als bei der ersten Partie, aber immer noch nicht zu vernachlässigen war. Die dritte Tiefenebene leistet ebenfalls einen geringen Beitrag, die Monotonie ist jedoch viel schlimmer und größere Tiefen haben grundsätzlich keinen Referenzwert.

Den Ungleichgewichtsparametern der drei Ebenen werden entsprechend den unterschiedlichen Beitragsniveaus unterschiedliche Gewichte zugewiesen. Die tatsächliche Prüfung zeigt, dass die Vorhersagefehler bei unterschiedlichen Berechnungsmethoden weiter reduziert werden.

bins = np.linspace(-1, 1, 50)
df['change'] = (df['price'].pct_change().shift(-1))/tick_size
df['I_bins'] = pd.cut(df['I'], bins, labels=bins[1:])
df['I_2'] = (df['bid_1_quantity'] - df['ask_1_quantity']) / (df['bid_1_quantity'] + df['ask_1_quantity'])
df['I_2_bins'] = pd.cut(df['I_2'], bins, labels=bins[1:])
df['I_3'] = (df['bid_2_quantity'] - df['ask_2_quantity']) / (df['bid_2_quantity'] + df['ask_2_quantity'])
df['I_3_bins'] = pd.cut(df['I_3'], bins, labels=bins[1:])
df['I_4'] = (df['bid_3_quantity'] - df['ask_3_quantity']) / (df['bid_3_quantity'] + df['ask_3_quantity'])
df['I_4_bins'] = pd.cut(df['I_4'], bins, labels=bins[1:])
fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(8, 5))


axes[0][0].plot(df.groupby('I_bins')['change'].mean())
axes[0][0].set_title('I')
axes[0][0].grid(True)

axes[0][1].plot(df.groupby('I_2_bins')['change'].mean())
axes[0][1].set_title('I 2')
axes[0][1].grid(True)

axes[1][0].plot(df.groupby('I_3_bins')['change'].mean())
axes[1][0].set_title('I 3')
axes[1][0].grid(True)

axes[1][1].plot(df.groupby('I_4_bins')['change'].mean())
axes[1][1].set_title('I 4')
axes[1][1].grid(True)
plt.tight_layout();

df['adjust_mid_price_4'] = df['mid_price'] + df['spread']*(df['I']+0.3)*(df['I']**4+0.7)/3.8
df['adjust_mid_price_5'] = df['mid_price'] + df['spread']*(0.7*df['I']+0.3*df['I_2'])/2
df['adjust_mid_price_6'] = df['mid_price'] + df['spread']*(0.7*df['I']+0.3*df['I_2'])**3/2
df['adjust_mid_price_7'] = df['mid_price'] + df['spread']*(0.7*df['I']+0.3*df['I_2']+0.3)*((0.7*df['I']+0.3*df['I_2'])**4+0.7)/3.8
df['adjust_mid_price_8'] = df['mid_price'] + df['spread']*(0.7*df['I']+0.2*df['I_2']+0.1*df['I_3']+0.3)*((0.7*df['I']+0.3*df['I_2']+0.1*df['I_3'])**4+0.7)/3.8

print('调整后的 mid_price_4的误差：', ((df['price']-df['adjust_mid_price_4'])**2).sum())
print('调整后的 mid_price_5的误差：', ((df['price']-df['adjust_mid_price_5'])**2).sum())
print('调整后的 mid_price_6的误差：', ((df['price']-df['adjust_mid_price_6'])**2).sum())
print('调整后的 mid_price_7的误差：', ((df['price']-df['adjust_mid_price_7'])**2).sum())
print('调整后的 mid_price_8的误差：', ((df['price']-df['adjust_mid_price_8'])**2).sum())

调整后的 mid_price_4的误差： 0.0047909595497071375
调整后的 mid_price_5的误差： 0.0047884350488318714
调整后的 mid_price_6的误差： 0.0047778319053133735
调整后的 mid_price_7的误差： 0.004773578540592192
调整后的 mid_price_8的误差： 0.004771415189297518

Transaktionsdaten berücksichtigen

Die Transaktionsdaten spiegeln direkt den Grad der Long- und Short-Positionen wider. Schließlich handelt es sich hierbei um eine Option, bei der es um echtes Geld geht, und die Kosten für die Auftragserteilung sind viel geringer, und es gibt sogar Fälle von vorsätzlichem Auftragsbetrug. Daher sollte sich die Strategie bei der Vorhersage des Mittelpreises auf Transaktionsdaten konzentrieren.

Definieren Sie unter Berücksichtigung des Formulars das Ungleichgewicht der durchschnittlichen Eingangsmenge der Bestellung. VI, Vb und Vs stellen jeweils die durchschnittliche Menge an Kauf- und Verkaufsaufträgen pro Einheitenereignis dar.

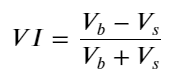
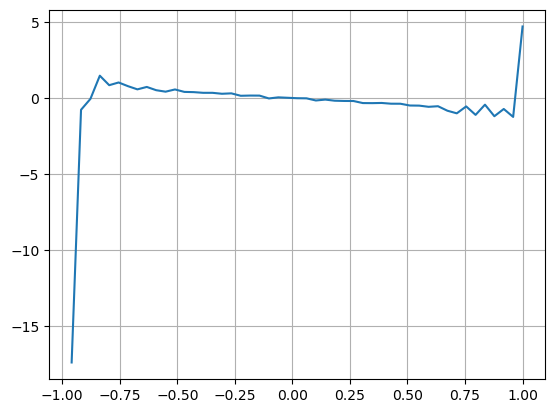
Die Ergebnisse zeigen, dass die Ankunftsmenge in einem kurzen Zeitraum am aussagekräftigsten ist, um Preisänderungen vorherzusagen. Wenn der VI zwischen (0,1-0,9) liegt, ist er negativ mit dem Preis korreliert, außerhalb des Bereichs ist er jedoch positiv mit dem Preis. Dies deutet darauf hin, dass der Markt, wenn er nicht extrem ist, hauptsächlich durch Schwankungen gekennzeichnet ist und die Preise zum Mittelwert zurückkehren. Wenn extreme Marktbedingungen auftreten, wie z. B. eine große Anzahl von Kaufaufträgen, die Verkaufsaufträge überwiegen, wird der Trend aus dem Trend herausgehen . Selbst wenn wir diese Situationen mit geringer Wahrscheinlichkeit ignorieren und einfach davon ausgehen, dass Trend und VI einer negativen linearen Beziehung genügen, verringert sich der Vorhersagefehler des Mittelpreises erheblich. Das a in der Formel stellt den Koeffizienten dar.

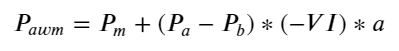
alpha=0.1

df['avg_buy_interval'] = None
df['avg_sell_interval'] = None
df.loc[df['is_buyer_maker'] == True, 'avg_buy_interval'] = df[df['is_buyer_maker'] == True]['transact_time'].diff().ewm(alpha=alpha).mean()
df.loc[df['is_buyer_maker'] == False, 'avg_sell_interval'] = df[df['is_buyer_maker'] == False]['transact_time'].diff().ewm(alpha=alpha).mean()

df['avg_buy_quantity'] = None
df['avg_sell_quantity'] = None
df.loc[df['is_buyer_maker'] == True, 'avg_buy_quantity'] = df[df['is_buyer_maker'] == True]['quantity'].ewm(alpha=alpha).mean()
df.loc[df['is_buyer_maker'] == False, 'avg_sell_quantity'] = df[df['is_buyer_maker'] == False]['quantity'].ewm(alpha=alpha).mean()

df['avg_buy_quantity'] = df['avg_buy_quantity'].fillna(method='ffill')
df['avg_sell_quantity'] = df['avg_sell_quantity'].fillna(method='ffill')
df['avg_buy_interval'] = df['avg_buy_interval'].fillna(method='ffill')
df['avg_sell_interval'] = df['avg_sell_interval'].fillna(method='ffill')

df['avg_buy_rate'] = 1000 / df['avg_buy_interval']
df['avg_sell_rate'] =1000 / df['avg_sell_interval']

df['avg_buy_volume'] = df['avg_buy_rate']*df['avg_buy_quantity']
df['avg_sell_volume'] = df['avg_sell_rate']*df['avg_sell_quantity']

df['I'] = (df['bid_0_quantity']- df['ask_0_quantity']) / (df['bid_0_quantity'] + df['ask_0_quantity'])
df['OI'] = (df['avg_buy_rate']-df['avg_sell_rate']) / (df['avg_buy_rate'] + df['avg_sell_rate'])
df['QI'] = (df['avg_buy_quantity']-df['avg_sell_quantity']) / (df['avg_buy_quantity'] + df['avg_sell_quantity'])
df['VI'] = (df['avg_buy_volume']-df['avg_sell_volume']) / (df['avg_buy_volume'] + df['avg_sell_volume'])

bins = np.linspace(-1, 1, 50)
df['VI_bins'] = pd.cut(df['VI'], bins, labels=bins[1:])
plt.plot(df.groupby('VI_bins')['change'].mean());
plt.grid(True)

df['adjust_mid_price'] = df['mid_price'] + df['spread']*df['I']/2
df['adjust_mid_price_9'] = df['mid_price'] + df['spread']*(-df['OI'])*2
df['adjust_mid_price_10'] = df['mid_price'] + df['spread']*(-df['VI'])*1.4

print('调整后的mid_price   的误差：', ((df['price']-df['adjust_mid_price'])**2).sum())
print('调整后的mid_price_9 的误差：', ((df['price']-df['adjust_mid_price_9'])**2).sum())
print('调整后的mid_price_10的误差：', ((df['price']-df['adjust_mid_price_10'])**2).sum())

调整后的mid_price   的误差： 0.0048373440193987035
调整后的mid_price_9 的误差： 0.004629586542840461
调整后的mid_price_10的误差： 0.004401790287167206

Umfassender Medianpreis

Da sowohl Pending Orders als auch Transaktionsdaten hilfreich für die Vorhersage des Mittelpreises sind, können diese beiden Parameter kombiniert werden. Die Gewichtungszuweisung ist hier willkürlich und berücksichtigt nicht die Randbedingungen. In extremen Fällen kann der vorhergesagte Mittelpreis nicht zwischen dem Kauf eines und dem Verkauf eines, aber solange der Fehler reduziert werden kann, spielen diese Details keine Rolle.

Schließlich sank der Vorhersagefehler von anfänglich 0,00487 auf 0,0043. Wir werden hier nicht ins Detail gehen. Über den mittleren Preis gibt es noch viel zu erforschen. Schließlich ist die Vorhersage des mittleren Preises die Vorhersage des Preises. Sie können es selbst ausprobieren .

#注意VI需要延后一个使用
df['price_change'] = np.log(df['price']/df['price'].rolling(40).mean())
df['CI'] = -1.5*df['VI'].shift()+0.7*(0.7*df['I']+0.2*df['I_2']+0.1*df['I_3'])**3 + 150*df['price_change'].shift(1)

df['adjust_mid_price_11'] = df['mid_price'] + df['spread']*(df['CI'])
print('调整后的mid_price_11的误差：', ((df['price']-df['adjust_mid_price_11'])**2).sum())

调整后的mid_price_11的误差： 0.00421125960463469

Zusammenfassen

In diesem Dokument werden Tiefendaten und Transaktionsdaten kombiniert, um die Berechnungsmethode des Mittelpreises weiter zu verbessern. Dieses Dokument bietet eine Methode zur Messung der Genauigkeit und verbessert die Genauigkeit der Vorhersage von Preisänderungen. Insgesamt sind die verschiedenen Parameter nicht sehr streng und dienen lediglich als Referenz. Mit einem genaueren Mittelpreis besteht der nächste Schritt darin, den Mittelpreis tatsächlich für Backtests anzuwenden. Dieser Teil hat auch viel Inhalt, daher werden wir die Aktualisierung für eine Weile einstellen.