In diesem Artikel schreiben wir eine Day-Trading-Strategie. Dabei kommt das klassische Handelskonzept der „Mean Reversion Trading Pairs“ zum Einsatz. In diesem Beispiel verwenden wir zwei börsengehandelte Fonds (ETFs), SPY und IWM, die an der New York Stock Exchange (NYSE) gehandelt werden und versuchen, die US-Aktienmarktindizes, den S&P 500 und den Russell 2000, darzustellen.“ .

Die Strategie erzeugt einen „Carry“, indem sie bei einem ETF Long-Positionen und bei einem anderen Short-Positionen einnimmt. Das Long-Short-Verhältnis kann auf viele Arten definiert werden, beispielsweise mithilfe statistischer Kointegrationszeitreihenmethoden. In diesem Szenario berechnen wir das Hedge-Verhältnis zwischen SPY und IWM mittels rollierender linearer Regression. Dadurch können wir einen „Spread“ zwischen SPY und IWM erstellen, der auf einen Z-Score normalisiert ist. Wenn der Z-Score einen bestimmten Schwellenwert überschreitet, wird ein Handelssignal generiert, weil wir davon ausgehen, dass dieser „Spread“ zum Mittelwert zurückkehren wird.

Die Begründung für diese Strategie liegt darin, dass sowohl SPY als auch IWM ungefähr dasselbe Marktszenario darstellen, nämlich die Aktienkursentwicklung einer Gruppe großer und kleiner US-Unternehmen. Die Prämisse ist, dass, wenn man die Theorie der “Mittelwertumkehr” der Preise akzeptiert, diese immer umkehren werden, weil “Ereignisse” den S&P500 und den Russell 2000 in einem sehr kurzen Zeitraum separat beeinflussen können, aber die “Zinsdifferenz” zwischen Sie werden immer zum normalen Mittelwert zurückkehren und die langfristigen Preisreihen der beiden werden immer kointegriert sein.

Strategie

Die Strategie wird wie folgt umgesetzt:

Daten – Erhalten Sie 1-minütige Candlestick-Charts von SPY und IWM von April 2007 bis Februar 2014.

Verarbeitung - Richten Sie die Daten richtig aus und löschen Sie die Balken, die zueinander fehlen. (Wenn eine Seite fehlt, werden beide Seiten gelöscht)

Spread – Das Hedge-Verhältnis zwischen zwei ETFs wird mithilfe einer rollierenden linearen Regression berechnet. Definiert als Beta-Regressionskoeffizient unter Verwendung eines Lookback-Fensters, das um 1 Balken nach vorne verschoben wird, und der Regressionskoeffizient wird neu berechnet. Daher wird das Sicherungsverhältnis βi, bi K-Linie verwendet, um die K-Linie zu verfolgen, indem der Kreuzungspunkt von bi-1-k zu bi-1 berechnet wird.

Z-Score – Der Wert des Standard-Spreads wird auf die übliche Weise berechnet. Dies bedeutet, dass der Mittelwert der Streuung (Stichprobe) abgezogen und durch die Standardabweichung der Streuung (Stichprobe) dividiert wird. Der Grund hierfür besteht darin, den Schwellenwertparameter leichter verständlich zu machen, da der Z-Score eine dimensionslose Größe ist. Ich habe absichtlich einen „Lookahead-Bias“ in die Berechnungen eingeführt, um zu zeigen, wie subtil dieser sein kann. Probieren Sie es aus!

Handel – Long-Signale werden generiert, wenn der negative Z-Score-Wert unter einen vorbestimmten (oder nachträglich optimierten) Schwellenwert fällt, während Short-Signale umgekehrt generiert werden. Wenn der absolute Wert des Z-Scores unter einen zusätzlichen Schwellenwert fällt, wird ein Signal zum Schließen der Position generiert. Für diese Strategie habe ich (etwas willkürlich) |z| = 2 als Eintrittsschwelle und |z| = 1 als Austrittsschwelle gewählt. Unter der Annahme, dass die Rückkehr zum Mittelwert bei der Spanne eine Rolle spielt, wird das Obige hoffentlich diese Arbitragebeziehung erfassen und einen schönen Gewinn erzielen.

Der vielleicht beste Weg, eine Strategie wirklich zu verstehen, besteht darin, sie tatsächlich umzusetzen. Der folgende Abschnitt beschreibt detailliert den vollständigen Python-Code (einzelne Datei), der zur Implementierung dieser Mean-Reversion-Strategie verwendet wurde. Ich habe ausführliche Codekommentare hinzugefügt, damit Sie es besser verstehen.

Python-Implementierung

Wie bei allen Python/Pandas-Tutorials muss Ihre Python-Umgebung wie in diesem Tutorial beschrieben eingerichtet werden. Sobald die Einrichtung abgeschlossen ist, besteht die erste Aufgabe darin, die erforderlichen Python-Bibliotheken zu importieren. Dies ist für die Verwendung von Matplotlib und Pandas erforderlich.

Die spezifischen Bibliotheksversionen, die ich verwende, sind wie folgt:

Python - 2.7.3 NumPy - 1.8.0 pandas - 0.12.0 matplotlib - 1.1.0

Lassen Sie uns fortfahren und diese Bibliotheken importieren:

# mr_spy_iwm.py

import matplotlib.pyplot as plt
import numpy as np
import os, os.path
import pandas as pd

Die folgende Funktion create_pairs_dataframe importiert zwei CSV-Dateien, die die Intraday-Candlesticks von zwei Symbolen enthalten. In unserem Fall wären dies SPY und IWM. Anschließend wird ein separates „Datenrahmenpaar“ erstellt, das die Indizes beider Originaldateien verwendet. Ihre Zeitstempel können aufgrund verpasster Transaktionen und Fehler variieren. Dies ist einer der Hauptvorteile der Verwendung einer Datenanalysebibliothek wie Pandas. Wir handhaben „Boilerplate“-Code auf sehr effiziente Weise.

# mr_spy_iwm.py
def create_pairs_dataframe(datadir, symbols):
    """Creates a pandas DataFrame containing the closing price
    of a pair of symbols based on CSV files containing a datetime
    stamp and OHLCV data."""
 
    # Open the individual CSV files and read into pandas DataFrames
    print "Importing CSV data..."
    sym1 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[0]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])
    sym2 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[1]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])
 
    # Create a pandas DataFrame with the close prices of each symbol
    # correctly aligned and dropping missing entries
    print "Constructing dual matrix for %s and %s..." % symbols    
    pairs = pd.DataFrame(index=sym1.index)
    pairs['%s_close' % symbols[0].lower()] = sym1['close']
    pairs['%s_close' % symbols[1].lower()] = sym2['close']
    pairs = pairs.dropna()
    return pairs

Der nächste Schritt besteht darin, eine rollierende lineare Regression zwischen SPY und IWM durchzuführen. In diesem Szenario ist IWM der Prädiktor („x“) und SPY die Antwort („y“). Ich habe ein Standard-Lookback-Fenster von 100 Kerzen festgelegt. Wie oben erwähnt, sind dies die Parameter der Strategie. Damit eine Strategie als robust angesehen werden kann, würden wir im Idealfall gerne einen Renditebericht sehen, der über den Rückblickzeitraum (oder eine andere Leistungskennzahl) konvex ist. Daher werden wir in einem späteren Stadium des Codes eine Sensitivitätsanalyse durchführen, indem wir den Rückblickzeitraum innerhalb des Umfangs variieren.

Nachdem Sie die gleitenden Betakoeffizienten im linearen Regressionsmodell für SPY-IWM berechnet haben, fügen Sie sie dem DataFrame-Paar hinzu und entfernen Sie die leeren Zeilen. Dadurch wird der erste Satz Kerzen erstellt, der dem gekürzten Maß der Rückblicklänge entspricht. Wir haben dann einen Spread zwischen den beiden ETFs erstellt, eine Einheit SPY und eine Einheit -βi von IWM. Dies ist offensichtlich kein realistisches Szenario, da wir nur eine kleine Menge IWM einsetzen, was in einer praktischen Implementierung nicht möglich ist.

Schließlich erstellen wir den Z-Score der Spanne, der durch Subtraktion des Mittelwerts der Spanne und Normalisierung mit der Standardabweichung der Spanne berechnet wird. Es ist wichtig zu beachten, dass hier eine ziemlich subtile „Vorausschau-Voreingenommenheit“ am Werk ist. Ich habe es absichtlich im Code gelassen, weil ich hervorheben wollte, wie leicht solche Fehler bei der Recherche passieren können. Berechnen Sie den Mittelwert und die Standardabweichung der gesamten gestreuten Zeitreihe. Wenn dies die wahre historische Genauigkeit widerspiegeln soll, können diese Informationen nicht abgerufen werden, da sie implizit Informationen aus der Zukunft verwenden. Daher sollten wir zur Berechnung des Z-Scores den gleitenden Mittelwert und die Standardabweichung verwenden.

# mr_spy_iwm.py
 
def calculate_spread_zscore(pairs, symbols, lookback=100):
    """Creates a hedge ratio between the two symbols by calculating
    a rolling linear regression with a defined lookback period. This
    is then used to create a z-score of the 'spread' between the two
    symbols based on a linear combination of the two."""
     
    # Use the pandas Ordinary Least Squares method to fit a rolling
    # linear regression between the two closing price time series
    print "Fitting the rolling Linear Regression..."
    model = pd.ols(y=pairs['%s_close' % symbols[0].lower()], 
                   x=pairs['%s_close' % symbols[1].lower()],
                   window=lookback)
 
    # Construct the hedge ratio and eliminate the first 
    # lookback-length empty/NaN period
    pairs['hedge_ratio'] = model.beta['x']
    pairs = pairs.dropna()
 
    # Create the spread and then a z-score of the spread
    print "Creating the spread/zscore columns..."
    pairs['spread'] = pairs['spy_close'] - pairs['hedge_ratio']*pairs['iwm_close']
    pairs['zscore'] = (pairs['spread'] - np.mean(pairs['spread']))/np.std(pairs['spread'])
    return pairs

Erstellen Sie in create_long_short_market_signals Handelssignale. Diese werden berechnet, indem der Z-Score-Wert gemessen wird, der einen Schwellenwert überschreitet. Wenn der absolute Wert des Z-Scores kleiner oder gleich einem anderen (kleineren) Schwellenwert ist, wird ein Signal zum Schließen der Position gegeben.

Um dies zu erreichen, muss für jede K-Linie festgelegt werden, ob die Handelsstrategie „Eröffnen“ oder „Schließen“ ist. Long_market und short_market sind zwei Variablen, die zur Verfolgung von Long- und Short-Positionen definiert sind. Leider ist der Rechenaufwand langsam, da die iterative Programmierung viel einfacher ist als ein vektorisierter Ansatz. Obwohl ein 1-Minuten-Candlestick-Chart ca. 700.000 Datenpunkte pro CSV-Datei erfordert, ist die Berechnung auf meinem alten Desktop immer noch relativ schnell!

Um über einen Pandas-DataFrame zu iterieren (eine zugegebenermaßen ungewöhnliche Operation), muss die Methode iterrows verwendet werden, die einen iterierbaren Generator bereitstellt:

# mr_spy_iwm.py
 
def create_long_short_market_signals(pairs, symbols, 
                                     z_entry_threshold=2.0, 
                                     z_exit_threshold=1.0):
    """Create the entry/exit signals based on the exceeding of 
    z_enter_threshold for entering a position and falling below
    z_exit_threshold for exiting a position."""
 
    # Calculate when to be long, short and when to exit
    pairs['longs'] = (pairs['zscore'] <= -z_entry_threshold)*1.0
    pairs['shorts'] = (pairs['zscore'] >= z_entry_threshold)*1.0
    pairs['exits'] = (np.abs(pairs['zscore']) <= z_exit_threshold)*1.0
 
    # These signals are needed because we need to propagate a
    # position forward, i.e. we need to stay long if the zscore
    # threshold is less than z_entry_threshold by still greater
    # than z_exit_threshold, and vice versa for shorts.
    pairs['long_market'] = 0.0
    pairs['short_market'] = 0.0
 
    # These variables track whether to be long or short while
    # iterating through the bars
    long_market = 0
    short_market = 0
 
    # Calculates when to actually be "in" the market, i.e. to have a
    # long or short position, as well as when not to be.
    # Since this is using iterrows to loop over a dataframe, it will
    # be significantly less efficient than a vectorised operation,
    # i.e. slow!
    print "Calculating when to be in the market (long and short)..."
    for i, b in enumerate(pairs.iterrows()):
        # Calculate longs
        if b[1]['longs'] == 1.0:
            long_market = 1            
        # Calculate shorts
        if b[1]['shorts'] == 1.0:
            short_market = 1
        # Calculate exists
        if b[1]['exits'] == 1.0:
            long_market = 0
            short_market = 0
        # This directly assigns a 1 or 0 to the long_market/short_market
        # columns, such that the strategy knows when to actually stay in!
        pairs.ix[i]['long_market'] = long_market
        pairs.ix[i]['short_market'] = short_market
    return pairs

In dieser Phase aktualisieren wir die Paare, sodass sie die tatsächlichen Long- und Short-Signale enthalten. So können wir feststellen, ob wir eine Position eröffnen müssen. Jetzt müssen wir ein Portfolio erstellen, um den Marktwert der Positionen zu verfolgen. Die erste Aufgabe besteht darin, eine Positionsspalte zu erstellen, die lange und kurze Signale kombiniert. Dies enthält eine Liste von Elementen von (1,0,-1), wobei 1 eine Long-Position darstellt, 0 keine Position darstellt (die geschlossen werden sollte) und -1 eine Short-Position darstellt. Die Spalten „sym1“ und „sym2“ stellen den Marktwert der SPY- und IWM-Positionen am Ende jeder Kerze dar.

Sobald die ETF-Marktwerte erstellt sind, summieren wir sie, um den Gesamtmarktwert am Ende jeder Kerze zu ermitteln. Es wird dann über die pct_change-Methode dieses Objekts in einen Rückgabewert umgewandelt. Nachfolgende Codezeilen bereinigen fehlerhafte Einträge (NaN- und inf-Elemente) und berechnen schließlich die vollständige Eigenkapitalkurve.

# mr_spy_iwm.py
 
def create_portfolio_returns(pairs, symbols):
    """Creates a portfolio pandas DataFrame which keeps track of
    the account equity and ultimately generates an equity curve.
    This can be used to generate drawdown and risk/reward ratios."""
     
    # Convenience variables for symbols
    sym1 = symbols[0].lower()
    sym2 = symbols[1].lower()
 
    # Construct the portfolio object with positions information
    # Note that minuses to keep track of shorts!
    print "Constructing a portfolio..."
    portfolio = pd.DataFrame(index=pairs.index)
    portfolio['positions'] = pairs['long_market'] - pairs['short_market']
    portfolio[sym1] = -1.0 * pairs['%s_close' % sym1] * portfolio['positions']
    portfolio[sym2] = pairs['%s_close' % sym2] * portfolio['positions']
    portfolio['total'] = portfolio[sym1] + portfolio[sym2]
 
    # Construct a percentage returns stream and eliminate all 
    # of the NaN and -inf/+inf cells
    print "Constructing the equity curve..."
    portfolio['returns'] = portfolio['total'].pct_change()
    portfolio['returns'].fillna(0.0, inplace=True)
    portfolio['returns'].replace([np.inf, -np.inf], 0.0, inplace=True)
    portfolio['returns'].replace(-1.0, 0.0, inplace=True)
 
    # Calculate the full equity curve
    portfolio['returns'] = (portfolio['returns'] + 1.0).cumprod()
    return portfolio

Die Hauptfunktion verbindet alles. Die Intraday-CSV-Dateien befinden sich im Datadir-Pfad. Denken Sie daran, den folgenden Code so zu ändern, dass er auf Ihr spezifisches Verzeichnis verweist.

Um zu bestimmen, wie empfindlich die Strategie auf den Rückblickzeitraum reagiert, muss eine Reihe von Rückblick-Leistungskennzahlen berechnet werden. Als Leistungskennzahl und Rückblickbereich habe ich den endgültigen Gesamtrenditeprozentsatz des Portfolios ausgewählt.[50.200] mit einer Erhöhung von 10. Sie können im folgenden Code sehen, dass die vorherige Funktion über diesen Bereich in eine For-Schleife eingeschlossen ist und die anderen Schwellenwerte gleich bleiben. Die letzte Aufgabe besteht darin, mit Matplotlib ein Liniendiagramm von Rückblicken gegenüber Renditen zu erstellen:

# mr_spy_iwm.py
 
if __name__ == "__main__":
    datadir = '/your/path/to/data/'  # Change this to reflect your data path!
    symbols = ('SPY', 'IWM')
 
    lookbacks = range(50, 210, 10)
    returns = []
 
    # Adjust lookback period from 50 to 200 in increments
    # of 10 in order to produce sensitivities
    for lb in lookbacks: 
        print "Calculating lookback=%s..." % lb
        pairs = create_pairs_dataframe(datadir, symbols)
        pairs = calculate_spread_zscore(pairs, symbols, lookback=lb)
        pairs = create_long_short_market_signals(pairs, symbols, 
                                                z_entry_threshold=2.0, 
                                                z_exit_threshold=1.0)
 
        portfolio = create_portfolio_returns(pairs, symbols)
        returns.append(portfolio.ix[-1]['returns'])
 
    print "Plot the lookback-performance scatterchart..."
    plt.plot(lookbacks, returns, '-o')
    plt.show()

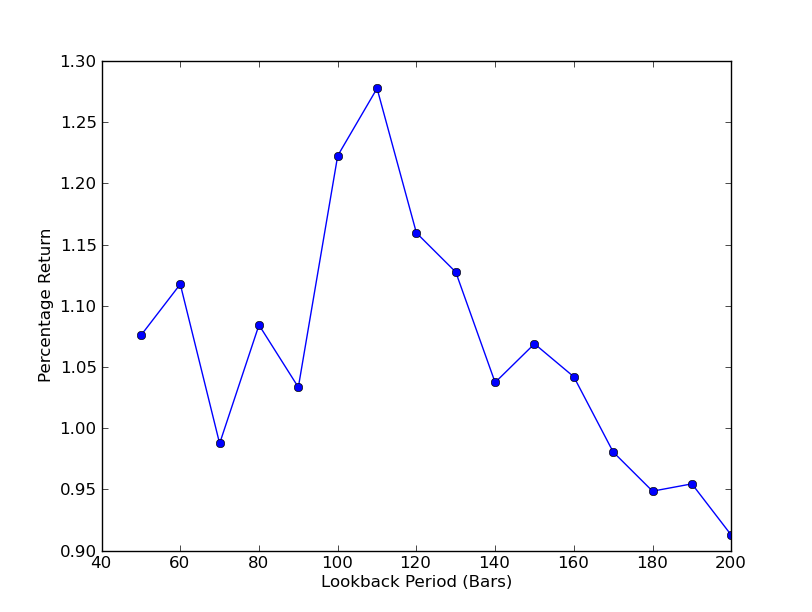
Jetzt können Sie eine Grafik der Rückblicke und Renditen sehen. Beachten Sie, dass es ein „globales“ Maximum für Lookbacks gibt, das 110 Balken entspricht. Wenn es Situationen gibt, in denen Rückblicke nichts mit Renditen zu tun haben, dann liegt das daran:

SPY-IWM Lineare Regression Hedge Ratio Lookback Period Sensitivitätsanalyse

Kein Backtesting-Artikel wäre ohne eine nach oben verlaufende Gewinnkurve vollständig! Wenn Sie also die kumulierten Gewinnrenditen im Zeitverlauf darstellen möchten, können Sie den folgenden Code verwenden. Es wird das endgültige Portfolio dargestellt, das aus der Lookback-Parameterstudie generiert wurde. Daher ist es notwendig, den Rückblick entsprechend dem Diagramm auszuwählen, das Sie visualisieren möchten. Dieses Diagramm stellt zum besseren Vergleich auch die Renditen von SPY im gleichen Zeitraum dar:

# mr_spy_iwm.py
 
    # This is still within the main function
    print "Plotting the performance charts..."
    fig = plt.figure()
    fig.patch.set_facecolor('white')
 
    ax1 = fig.add_subplot(211,  ylabel='%s growth (%%)' % symbols[0])
    (pairs['%s_close' % symbols[0].lower()].pct_change()+1.0).cumprod().plot(ax=ax1, color='r', lw=2.)
 
    ax2 = fig.add_subplot(212, ylabel='Portfolio value growth (%%)')
    portfolio['returns'].plot(ax=ax2, lw=2.)
 
    fig.show()

Das nachstehende Eigenkapitalkurvendiagramm hat einen Rückblickzeitraum von 100 Tagen:

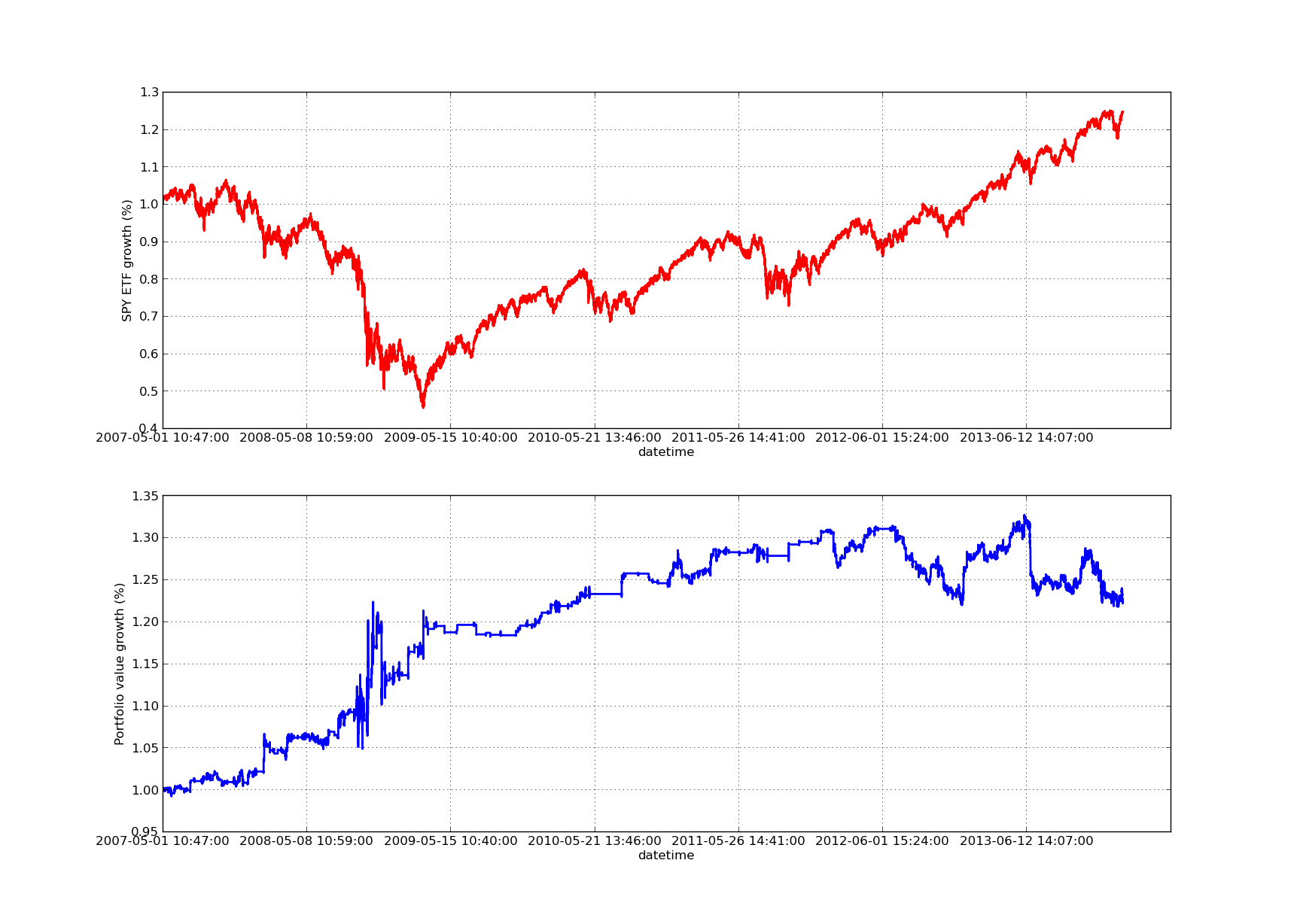
SPY-IWM Lineare Regression Hedge Ratio Lookback Period Sensitivitätsanalyse

Beachten Sie, dass der SPY-Rückgang während der Finanzkrise 2009 ziemlich groß war. Auch die Strategie durchlebt in dieser Phase eine turbulente Phase. Beachten Sie auch, dass sich die Performance im letzten Jahr verschlechtert hat, da der SPY in diesem Zeitraum einen starken Trend aufwies, der dem S&P 500 ähnelt.

Beachten Sie, dass wir bei der Berechnung der Z-Score-Streuung immer noch den „Lookahead-Bias“ berücksichtigen müssen. Darüber hinaus werden alle diese Berechnungen ohne Transaktionskosten durchgeführt. Wenn diese Faktoren berücksichtigt werden, ist die Leistung dieser Strategie zwangsläufig schlecht. Sowohl die Gebühren als auch die Slippage sind derzeit unbestimmt. Darüber hinaus werden bei dieser Strategie Teilanteile des ETFs gehandelt, was ebenfalls höchst unrealistisch ist.

In einem zukünftigen Artikel werden wir einen komplexeren ereignisgesteuerten Backtester erstellen, der alle oben genannten Punkte berücksichtigt und uns mehr Vertrauen in unsere Eigenkapitalkurve und Leistungsindikatoren gibt.