Pairs Trading ist ein hervorragendes Beispiel für die Entwicklung einer Handelsstrategie auf Grundlage mathematischer Analysen. In diesem Artikel zeigen wir, wie Sie Daten nutzen können, um eine Pairs-Trading-Strategie zu erstellen und zu automatisieren.

Grundprinzipien

Angenommen, Sie haben ein Anlagepaar X und Y, denen eine gewisse Korrelation zugrunde liegt, z. B. dass beide Unternehmen dasselbe Produkt herstellen, wie etwa Pepsi und Coca-Cola. Sie möchten, dass das Preisverhältnis oder die Basis (auch Spread genannt) zwischen den beiden im Laufe der Zeit konstant bleibt. Der Spread zwischen den beiden Paaren kann jedoch von Zeit zu Zeit aufgrund vorübergehender Änderungen von Angebot und Nachfrage abweichen, wie z. B. aufgrund großer Kauf-/Verkaufsaufträge für ein Anlageziel, einer Reaktion auf wichtige Neuigkeiten über eines der Unternehmen usw. In diesem Fall bewegt sich eine Investition nach oben und die andere nach unten im Verhältnis zueinander. Wenn Sie davon ausgehen, dass sich diese Divergenz mit der Zeit normalisiert, können Sie eine Handelsmöglichkeit (oder Arbitragemöglichkeit) erkennen. Solche Arbitragemöglichkeiten gibt es überall auf dem Markt für digitale Währungen oder auf dem inländischen Rohstoff-Terminmarkt, beispielsweise in der Beziehung zwischen BTC und sicheren Anlagen oder in der Beziehung zwischen Sojabohnenmehl, Sojabohnenöl und Sojabohnensorten in Terminkontrakten.

Wenn es einen vorübergehenden Preisunterschied gibt, wird der Handel die überdurchschnittliche Investition (die Investition, die gestiegen ist) verkaufen und die unterdurchschnittliche Investition (die Investition, die gefallen ist) kaufen. Sie können sicher sein, dass es einen Unterschied zwischen den beiden Investitionen gibt. Die Der Spread wird sich letztendlich darin niederschlagen, dass die überdurchschnittliche Anlage zurückfällt oder die unterdurchschnittliche Anlage wieder steigt oder beides. Ihr Handel wird in allen diesen Szenarien Gewinn bringen. Wenn die Investitionen gemeinsam steigen oder fallen, ohne dass sich die Differenz zwischen ihnen ändert, werden Sie weder Geld verdienen noch verlieren.

Daher ist der Paarhandel eine marktneutrale Handelsstrategie, die es Händlern ermöglicht, von nahezu jeder Marktlage zu profitieren: Aufwärtstrend, Abwärtstrend oder Seitwärtsbewegung.

Erklären Sie das Konzept: zwei hypothetische Anlageziele

• Aufbau unserer Forschungsumgebung auf der Inventor Quantitative Platform

Um reibungslos arbeiten zu können, müssen wir zunächst unsere Forschungsumgebung aufbauen. In diesem Artikel verwenden wir die Inventor Quantitative Platform (FMZ.COM), um die Forschungsumgebung aufzubauen, hauptsächlich, damit wir die praktische und schnelle API nutzen können Schnittstelle und Kapselung dieser Plattform später. Komplettes Docker-System.

Im offiziellen Namen der Inventor Quantitative Platform wird dieses Docker-System als Hostsystem bezeichnet.

Weitere Informationen zum Bereitstellen von Hosts und Robotern finden Sie in meinem vorherigen Artikel: https://www.fmz.com/bbs-topic/4140

Leser, die ihren eigenen Cloud-Computing-Server-Bereitstellungshost erwerben möchten, können diesen Artikel lesen: https://www.fmz.com/bbs-topic/2848

Nach der erfolgreichen Bereitstellung des Cloud-Computing-Dienstes und des Hostsystems installieren wir das leistungsstärkste Python-Tool: Anaconda

Um alle für diesen Artikel relevanten Programmumgebungen (abhängige Bibliotheken, Versionsverwaltung etc.) zu realisieren, bietet sich am einfachsten die Verwendung von Anaconda an. Es handelt sich um ein gepacktes Python-Data-Science-Ökosystem und einen Abhängigkeitsmanager.

Informationen zur Installationsmethode von Anaconda finden Sie im offiziellen Handbuch von Anaconda: https://www.anaconda.com/distribution/

In diesem Artikel werden auch Numpy und Pandas verwendet, zwei sehr beliebte und wichtige Bibliotheken für wissenschaftliche Berechnungen mit Python.

Für die oben genannten grundlegenden Arbeiten können Sie auch meinen vorherigen Artikel lesen, in dem die Einrichtung der Anaconda-Umgebung und der beiden Bibliotheken Numpy und Pandas beschrieben wird. Weitere Einzelheiten finden Sie unter: https://www.fmz.com/digest- Thema/4169

Als nächstes verwenden wir Code, um „zwei hypothetische Investitionsziele“ zu implementieren.

import numpy as np
import pandas as pd

import statsmodels
from statsmodels.tsa.stattools import coint
# just set the seed for the random number generator
np.random.seed(107)

import matplotlib.pyplot as plt

Ja, wir werden auch matplotlib verwenden, eine sehr bekannte Diagrammbibliothek in Python.

Lassen Sie uns ein hypothetisches Anlagevermögen X generieren und die Darstellung seiner täglichen Renditen mithilfe einer Normalverteilung simulieren. Wir führen dann eine kumulative Summe durch, um den täglichen X-Wert zu erhalten.

# Generate daily returns
Xreturns = np.random.normal(0, 1, 100) 
# sum them and shift all the prices up
X = pd.Series(np.cumsum(
    Xreturns), name='X') 
    + 50
X.plot(figsize=(15,7))
plt.show()

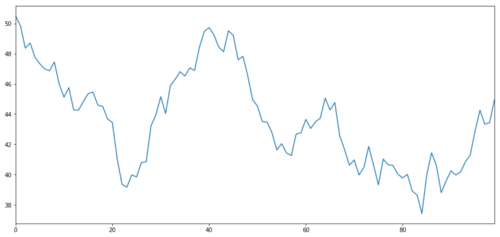
Anlageziel X, simulieren und ermitteln Sie dessen tägliche Rendite durch Normalverteilung

Jetzt generieren wir Y, das stark mit X korreliert, sodass sich der Preis von Y sehr ähnlich zu den Änderungen in X bewegen sollte. Wir modellieren dies, indem wir X nehmen, es nach oben verschieben und etwas zufälliges Rauschen aus einer Normalverteilung hinzufügen.

noise = np.random.normal(0, 1, 100)
Y = X + 5 + noise
Y.name = 'Y'
pd.concat([X, Y], axis=1).plot(figsize=(15,7))
plt.show()

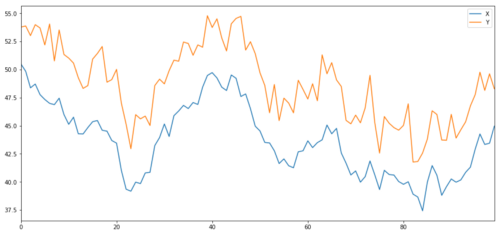
Kointegration der Anlageziele X und Y

Kointegration

Kointegration ist der Korrelation sehr ähnlich, was bedeutet, dass das Verhältnis zwischen zwei Datenreihen um den Mittelwert herum schwankt. Die beiden Reihen Y und X ergeben folgendes Bild:

Y = ⍺ X + e

wobei ⍺ ein konstantes Verhältnis und e das Rauschen ist.

Bei einem Handelspaar zwischen zwei Zeitreihen muss der erwartete Wert des Verhältnisses im Zeitverlauf zum Mittelwert konvergieren, d. h. sie sollten kointegriert sein. Die oben erstellten Zeitreihen sind kointegriert. Wir zeichnen jetzt den Maßstab zwischen den beiden, damit wir sehen können, wie es aussehen wird.

(Y/X).plot(figsize=(15,7)) 
plt.axhline((Y/X).mean(), color='red', linestyle='--') 
plt.xlabel('Time')
plt.legend(['Price Ratio', 'Mean'])
plt.show()

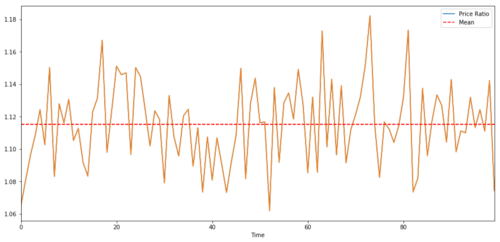
Das Verhältnis und der Durchschnitt der Preise zweier kointegrierter Investitionen

Kointegrationstest

Eine bequeme Möglichkeit, dies zu testen, ist die Verwendung von statsmodels.tsa.stattools. Wir sollten einen sehr niedrigen p-Wert sehen, da wir künstlich zwei Datenreihen erstellt haben, die so kointegriert wie möglich sind.

# compute the p-value of the cointegration test
# will inform us as to whether the ratio between the 2 timeseries is stationary
# around its mean
score, pvalue, _ = coint(X,Y)
print pvalue

Das Ergebnis lautet: 1,81864477307e-17

Hinweis: Korrelation und Kointegration

Obwohl Korrelation und Kointegration in der Theorie ähnlich sind, sind sie nicht dasselbe. Sehen wir uns Beispiele für Datenreihen an, die korreliert, aber nicht kointegriert sind und umgekehrt. Lassen Sie uns zunächst die Korrelation der gerade erstellten Reihe überprüfen.

X.corr(Y)

Das Ergebnis ist: 0,951

Dieser Wert ist erwartungsgemäß sehr hoch. Aber was ist mit zwei Reihen, die korreliert, aber nicht kointegriert sind? Ein einfaches Beispiel sind zwei Datenreihen, die auseinandergehen.

ret1 = np.random.normal(1, 1, 100)
ret2 = np.random.normal(2, 1, 100)

s1 = pd.Series( np.cumsum(ret1), name='X')
s2 = pd.Series( np.cumsum(ret2), name='Y')

pd.concat([s1, s2], axis=1 ).plot(figsize=(15,7))
plt.show()
print 'Correlation: ' + str(X_diverging.corr(Y_diverging))
score, pvalue, _ = coint(X_diverging,Y_diverging)
print 'Cointegration test p-value: ' + str(pvalue)

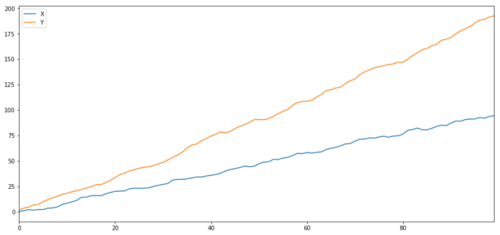
Zwei verwandte Serien (nicht kointegriert)

Korrelationskoeffizient: 0,998 Kointegrationstest p-Wert: 0,258

Einfache Beispiele für Kointegration ohne Korrelation sind eine normalverteilte Reihe und eine Rechteckwelle.

Y2 = pd.Series(np.random.normal(0, 1, 800), name='Y2') + 20
Y3 = Y2.copy()

Y3[0:100] = 30
Y3[100:200] = 10
Y3[200:300] = 30
Y3[300:400] = 10
Y3[400:500] = 30
Y3[500:600] = 10
Y3[600:700] = 30
Y3[700:800] = 10
Y2.plot(figsize=(15,7))
Y3.plot()
plt.ylim([0, 40])
plt.show()
# correlation is nearly zero
print 'Correlation: ' + str(Y2.corr(Y3))
score, pvalue, _ = coint(Y2,Y3)
print 'Cointegration test p-value: ' + str(pvalue)

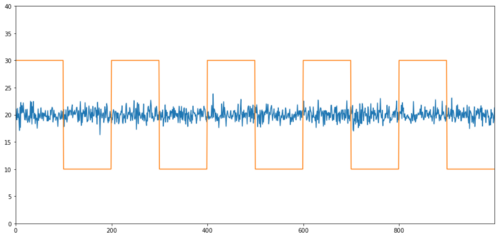
Korrelation: 0,007546 Kointegrationstest p-Wert: 0,0

Die Korrelation ist sehr gering, aber der p-Wert zeigt eine perfekte Kointegration!

Wie funktioniert Paarhandel?

Da sich zwei kointegrierte Zeitreihen (wie etwa X und Y oben) aufeinander zu und voneinander weg bewegen, kommt es manchmal zu Situationen, in denen es eine hohe und eine niedrige Basis gibt. Wir führen Paarhandel durch, indem wir eine Anlage kaufen und eine andere verkaufen. Auf diese Weise verdienen wir weder Geld noch verlieren wir Geld, wenn die beiden Anlageziele gleichzeitig fallen oder steigen. Das heißt, wir sind marktneutral.

Wenn wir zu X und Y in Y = ⍺ X + e oben zurückkehren, verdienen wir Geld, indem wir das Verhältnis (Y/X) um seinen Mittelwert ⍺ bewegen. Dazu stellen wir fest, dass wenn X Wenn der Wert von ⍺ zu hoch oder zu niedrig, der Wert von ⍺ ist zu hoch oder zu niedrig:

• Langes Verhältnis: Dies ist der Fall, wenn das Verhältnis ⍺ klein ist und wir erwarten, dass es größer wird. Im obigen Beispiel eröffnen wir eine Position, indem wir Long Y und Short X gehen.

• Short Ratio: Dies ist der Fall, wenn das Verhältnis ⍺ groß ist und wir erwarten, dass es kleiner wird. Im obigen Beispiel eröffnen wir eine Position, indem wir Y shorten und X long gehen.

Beachten Sie, dass wir immer eine „abgesicherte Position“ haben: Wenn die zugrunde liegende Long-Position an Wert verliert, verdient die Short-Position Geld und umgekehrt. Wir sind also immun gegen allgemeine Marktbewegungen.

Wenn sich die Vermögenswerte X und Y relativ zueinander bewegen, verdienen oder verlieren wir Geld.

Verwenden Sie Daten, um Transaktionen mit ähnlichem Verhalten zu finden

Am besten beginnen Sie hierzu mit den Trades, bei denen Sie eine Kointegration vermuten, und führen statistische Tests durch. Wenn Sie einen statistischen Test für alle Handelspaare durchführen, werden SieVerzerrung durch MehrfachvergleicheOpfer von.

Verzerrung durch Mehrfachvergleichebezieht sich auf die Situation, in der die Wahrscheinlichkeit der fälschlichen Generierung eines signifikanten p-Werts beim Ausführen vieler Tests steigt, da wir eine große Anzahl von Tests durchführen müssen. Wenn wir diesen Test 100 Mal mit zufälligen Daten ausführen, sollten wir 5 p-Werte unter 0,05 sehen. Wenn Sie n Instrumente auf Kointegration vergleichen, führen Sie n(n-1)/2 Vergleiche durch und sehen viele falsche p-Werte, die mit zunehmender Größe Ihrer Teststichprobe zunehmen. Und immer größer werden. Um dies zu vermeiden, wählen Sie einige Handelspaare aus, bei denen Sie Grund zu der Annahme haben, dass eine Kointegration wahrscheinlich ist, und testen Sie diese dann einzeln. Dadurch wird dieVerzerrung durch Mehrfachvergleiche。

Versuchen wir also, einige Instrumente zu finden, die Kointegration aufweisen. Nehmen wir einen Korb von US-amerikanischen Technologieaktien mit großer Marktkapitalisierung im S&P 500. Diese Instrumente sind in ähnlichen Marktsegmenten tätig und weisen Kointegration auf. Preis. Wir scannen die Liste der Handelsinstrumente und testen alle Paare auf Kointegration.

Die zurückgegebene Kointegrationstestergebnismatrix, die p-Wertmatrix und alle paarweisen Übereinstimmungen mit einem p-Wert von weniger als 0,05 sind enthalten.Da diese Methode anfällig für Verzerrungen durch Mehrfachvergleiche ist, muss in der Praxis eine zweite Validierung durchgeführt werden. Der Einfachheit halber ignorieren wir dies in den Beispielen dieses Artikels.

def find_cointegrated_pairs(data):
    n = data.shape[1]
    score_matrix = np.zeros((n, n))
    pvalue_matrix = np.ones((n, n))
    keys = data.keys()
    pairs = []
    for i in range(n):
        for j in range(i+1, n):
            S1 = data[keys[i]]
            S2 = data[keys[j]]
            result = coint(S1, S2)
            score = result[0]
            pvalue = result[1]
            score_matrix[i, j] = score
            pvalue_matrix[i, j] = pvalue
            if pvalue < 0.02:
                pairs.append((keys[i], keys[j]))
    return score_matrix, pvalue_matrix, pairs

Hinweis: Wir haben den Markt-Benchmark (SPX) in unsere Daten aufgenommen - der Markt treibt den Fluss vieler Instrumente an und oft findet man zwei Instrumente, die kointegriert zu sein scheinen; in Wirklichkeit sind sie aber nicht miteinander kointegriert, sondern Kointegration mit der Markt. Dies nennt man Störvariable. Es ist wichtig, die Marktbeteiligung bei jeder Beziehung, die Sie finden, zu untersuchen.

from backtester.dataSource.yahoo_data_source import YahooStockDataSource
from datetime import datetime
startDateStr = '2007/12/01'
endDateStr = '2017/12/01'
cachedFolderName = 'yahooData/'
dataSetId = 'testPairsTrading'
instrumentIds = ['SPY','AAPL','ADBE','SYMC','EBAY','MSFT','QCOM',
                 'HPQ','JNPR','AMD','IBM']
ds = YahooStockDataSource(cachedFolderName=cachedFolderName,
                            dataSetId=dataSetId,
                            instrumentIds=instrumentIds,
                            startDateStr=startDateStr,
                            endDateStr=endDateStr,
                            event='history')
data = ds.getBookDataByFeature()['Adj Close']
data.head(3)

Versuchen wir nun, mit unserer Methode kointegrierte Handelspaare zu finden.

# Heatmap to show the p-values of the cointegration test
# between each pair of stocks
scores, pvalues, pairs = find_cointegrated_pairs(data)
import seaborn
m = [0,0.2,0.4,0.6,0.8,1]
seaborn.heatmap(pvalues, xticklabels=instrumentIds, 
                yticklabels=instrumentIds, cmap=’RdYlGn_r’, 
                mask = (pvalues >= 0.98))
plt.show()
print pairs

[('ADBE', 'MSFT')]

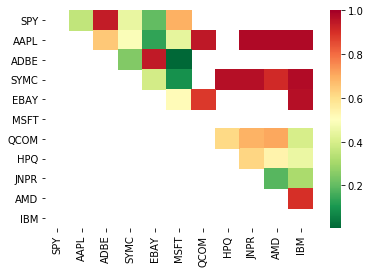
Es sieht so aus, als ob „ADBE“ und „MSFT“ kointegriert sind. Werfen wir einen Blick auf den Preis, um sicherzustellen, dass es wirklich Sinn macht.

S1 = data['ADBE']
S2 = data['MSFT']
score, pvalue, _ = coint(S1, S2)
print(pvalue)
ratios = S1 / S2
ratios.plot()
plt.axhline(ratios.mean())
plt.legend([' Ratio'])
plt.show()

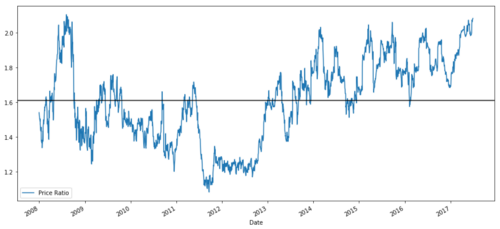
Diagramm des Preisverhältnisses zwischen MSFT und ADBE von 2008 bis 2017

Dieses Verhältnis sieht tatsächlich wie ein stabiler Durchschnitt aus. Absolute Verhältnisse sind statistisch nicht sehr nützlich. Es ist hilfreicher, unser Signal zu normalisieren, indem wir es als Z-Score betrachten. Der Z-Score wird wie folgt definiert:

Z Score (Value) = (Value — Mean) / Standard Deviation

warnen

In der Praxis versuchen wir normalerweise, eine gewisse Erweiterung auf die Daten anzuwenden, aber nur, wenn die Daten normal verteilt sind. Da jedoch viele Finanzdaten nicht normal verteilt sind, müssen wir sehr vorsichtig sein und bei der Erstellung von Statistiken nicht einfach von Normalität oder einer bestimmten Verteilung ausgehen. Die wahre Verteilung der Verhältnisse kann dicke Enden aufweisen und Daten, die zu Extremen tendieren, können unser Modell verwirren und zu großen Verlusten führen.

def zscore(series):
    return (series - series.mean()) / np.std(series)

zscore(ratios).plot()
plt.axhline(zscore(ratios).mean())
plt.axhline(1.0, color=’red’)
plt.axhline(-1.0, color=’green’)
plt.show()

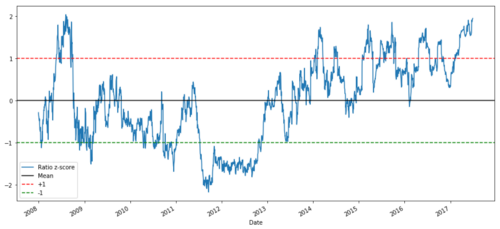
Z-Preisverhältnis zwischen MSFT und ADBE von 2008 bis 2017

Jetzt ist es einfacher zu erkennen, wie sich das Verhältnis um den Mittelwert bewegt, aber manchmal neigt es zu großen Abweichungen vom Mittelwert, die wir ausnutzen können.

Nachdem wir nun die Grundlagen einer Paarhandelsstrategie besprochen und Kointegrationsziele auf Grundlage der Preishistorie ermittelt haben, versuchen wir, ein Handelssignal zu entwickeln. Lassen Sie uns zunächst die Schritte zur Entwicklung von Handelssignalen mithilfe von Datentechniken durchgehen:

• Zuverlässige Daten sammeln und Daten bereinigen

• Erstellen Sie Funktionen aus Daten, um Handelssignale/-logik zu identifizieren

• Merkmale können gleitende Durchschnitte oder Preisdaten, Korrelationen oder Verhältnisse komplexerer Signale sein – kombinieren Sie diese, um neue Merkmale zu erstellen

• Nutzen Sie diese Funktionen, um Handelssignale zu generieren, d.h. welche Signale Kauf-, Verkaufs- oder Short-Positionen sind

Glücklicherweise haben wir die Inventor Quantitative Platform (fmz.com), die die oben genannten vier Aspekte für uns erfüllt. Dies ist ein großer Segen für Strategieentwickler. Wir können unsere Energie und Zeit auf Strategielogik, Design und Funktionserweiterung verwenden.

Auf der Inventor Quantitative Platform gibt es vorgefertigte Schnittstellen zu verschiedenen gängigen Börsen. Wir müssen diese API-Schnittstellen nur aufrufen. Der Rest der zugrunde liegenden Implementierungslogik wurde von einem professionellen Team verfeinert.

Der logischen Vollständigkeit halber und zur Erläuterung der Prinzipien werden wir diese zugrunde liegende Logik ausführlich darstellen. Im tatsächlichen Betrieb können die Leser jedoch direkt die API-Schnittstelle von Inventor Quant aufrufen, um die oben genannten vier Aspekte zu vervollständigen.

Lasst uns anfangen:

Schritt 1: Problem beschreiben

Hier versuchen wir, ein Signal zu erstellen, das uns sagt, ob das Verhältnis im nächsten Moment ein Kauf oder ein Verkauf sein wird, was unsere Prädiktorvariable Y ist:

Y = Ratio is buy (1) or sell (-1)

Y(t)= Sign(Ratio(t+1) — Ratio(t))

Beachten Sie, dass wir nicht den tatsächlichen Preis des Basiswerts oder sogar den tatsächlichen Wert des Verhältnisses vorhersagen müssen (obwohl wir das können), sondern als Nächstes nur die Richtung des Verhältnisses vorhersagen müssen.

Schritt 2: Sammeln Sie zuverlässige und genaue Daten

Inventor Quant ist dein Freund! Sie geben einfach die Instrumente an, mit denen Sie handeln möchten, und die Datenquelle, die Sie verwenden möchten. Anschließend werden die erforderlichen Daten extrahiert und für Dividenden- und Instrumentenaufteilungen bereinigt. Unsere Daten hier sind also bereits sehr sauber.

Wir haben die folgenden Daten von Yahoo Finance für Handelstage der letzten 10 Jahre verwendet (ungefähr 2.500 Datenpunkte): Eröffnung, Schluss, Hoch, Tief und Volumen

Schritt 3: Aufteilen der Daten

Vergessen Sie nicht diesen sehr wichtigen Schritt zum Testen der Genauigkeit Ihres Modells. Wir verwenden die folgende Aufteilung der Daten für Training/Validierung/Test

• Training 7 years ~ 70%

• Test ~ 3 years 30%

ratios = data['ADBE'] / data['MSFT']
print(len(ratios))
train = ratios[:1762]
test = ratios[1762:]

Idealerweise würden wir auch einen Validierungssatz erstellen, aber das tun wir vorerst nicht.

Schritt 4: Feature Engineering

Welche Funktionen könnten damit verbunden sein? Wir möchten die Richtung der Verhältnisänderung vorhersagen. Wir haben gesehen, dass unsere beiden Instrumente kointegriert sind, sodass dieses Verhältnis dazu neigt, sich zu verschieben und zum Mittelwert zurückzukehren. Es scheint, dass unsere Funktion eine Art Maß für den Mittelwert des Verhältnisses sein sollte, und die Differenz zwischen dem aktuellen Wert und dem Mittelwert kann unser Handelssignal generieren.

Wir nutzen folgende Funktionen:

• 60-Tage-Gleitendes-Durchschnittsverhältnis: Ein Maß für den gleitenden Durchschnitt

• 5-Tage-Gleitendes-Durchschnittsverhältnis: Ein Maß für den aktuellen Wert des Durchschnitts

• 60-Tage-Standardabweichung

• Z-Score: (5-Tage-MA – 60-Tage-MA) / 60-Tage-SD

ratios_mavg5 = train.rolling(window=5,
                               center=False).mean()
ratios_mavg60 = train.rolling(window=60,
                               center=False).mean()
std_60 = train.rolling(window=60,
                        center=False).std()
zscore_60_5 = (ratios_mavg5 - ratios_mavg60)/std_60
plt.figure(figsize=(15,7))
plt.plot(train.index, train.values)
plt.plot(ratios_mavg5.index, ratios_mavg5.values)
plt.plot(ratios_mavg60.index, ratios_mavg60.values)
plt.legend(['Ratio','5d Ratio MA', '60d Ratio MA'])
plt.ylabel('Ratio')
plt.show()

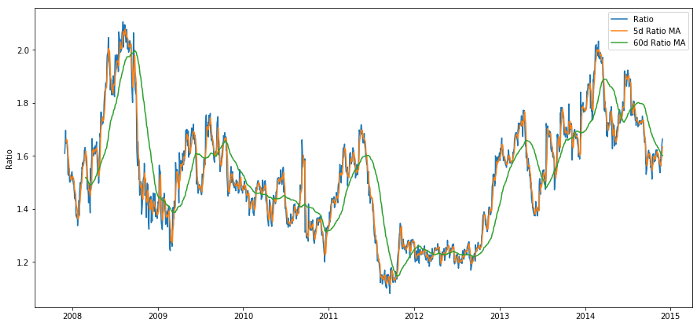
Preisverhältnis von 60d und 5d MA

plt.figure(figsize=(15,7))
zscore_60_5.plot()
plt.axhline(0, color='black')
plt.axhline(1.0, color='red', linestyle='--')
plt.axhline(-1.0, color='green', linestyle='--')
plt.legend(['Rolling Ratio z-Score', 'Mean', '+1', '-1'])
plt.show()

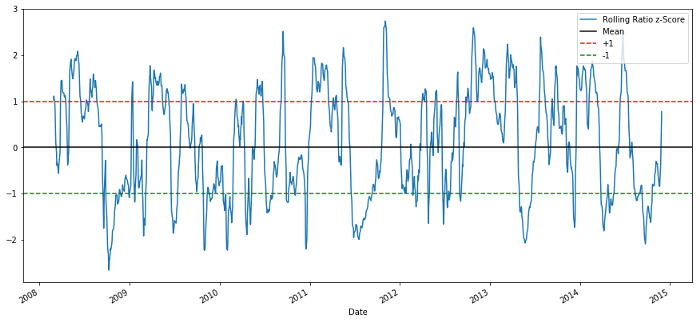
60-5 Z-Score-Preisverhältnis

Der Z-Score des gleitenden Mittelwerts bringt die zum Mittelwert zurückkehrende Natur des Verhältnisses deutlich zum Ausdruck!

Schritt 5: Modellauswahl

Beginnen wir mit einem sehr einfachen Modell. Wenn wir uns das Z-Score-Diagramm ansehen, können wir erkennen, dass immer dann ein Rückgang auftritt, wenn der Z-Score zu hoch oder zu niedrig ist. Verwenden wir +1/-1 als Schwellenwerte, um zu hoch und zu niedrig zu definieren. Anschließend können wir das folgende Modell zur Generierung von Handelssignalen verwenden:

• Wenn z unter -1,0 liegt, ist das Verhältnis kaufen (1), da wir erwarten, dass z auf 0 zurückkehrt, sodass das Verhältnis steigt

• Wenn z über 1,0 liegt, ist das Verhältnis verkaufen (-1), weil wir erwarten, dass z auf 0 zurückkehrt und somit das Verhältnis sinkt

Schritt 6: Training, Validierung und Optimierung

Sehen wir uns abschließend die tatsächliche Auswirkung unseres Modells auf reale Daten an. Schauen wir uns an, wie sich dieses Signal in realen Verhältnissen verhält

# Plot the ratios and buy and sell signals from z score
plt.figure(figsize=(15,7))
train[60:].plot()
buy = train.copy()
sell = train.copy()
buy[zscore_60_5>-1] = 0
sell[zscore_60_5<1] = 0
buy[60:].plot(color=’g’, linestyle=’None’, marker=’^’)
sell[60:].plot(color=’r’, linestyle=’None’, marker=’^’)
x1,x2,y1,y2 = plt.axis()
plt.axis((x1,x2,ratios.min(),ratios.max()))
plt.legend([‘Ratio’, ‘Buy Signal’, ‘Sell Signal’])
plt.show()

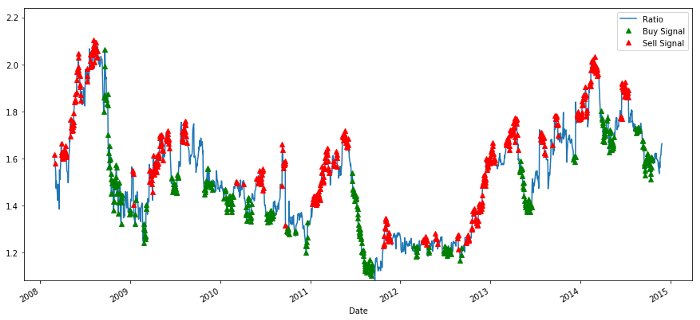
Kauf- und Verkaufspreis-Verhältnissignale

Dieses Signal erscheint sinnvoll. Wir scheinen das Verhältnis zu verkaufen, wenn es hoch ist oder steigt (rote Punkte), und es zurückzukaufen, wenn es niedrig ist (grüne Punkte) und fällt. Was bedeutet dies für den konkreten Gegenstand unserer Transaktionen? mal sehen

# Plot the prices and buy and sell signals from z score
plt.figure(figsize=(18,9))
S1 = data['ADBE'].iloc[:1762]
S2 = data['MSFT'].iloc[:1762]
S1[60:].plot(color='b')
S2[60:].plot(color='c')
buyR = 0*S1.copy()
sellR = 0*S1.copy()
# When buying the ratio, buy S1 and sell S2
buyR[buy!=0] = S1[buy!=0]
sellR[buy!=0] = S2[buy!=0]
# When selling the ratio, sell S1 and buy S2 
buyR[sell!=0] = S2[sell!=0]
sellR[sell!=0] = S1[sell!=0]
buyR[60:].plot(color='g', linestyle='None', marker='^')
sellR[60:].plot(color='r', linestyle='None', marker='^')
x1,x2,y1,y2 = plt.axis()
plt.axis((x1,x2,min(S1.min(),S2.min()),max(S1.max(),S2.max())))
plt.legend(['ADBE','MSFT', 'Buy Signal', 'Sell Signal'])
plt.show()

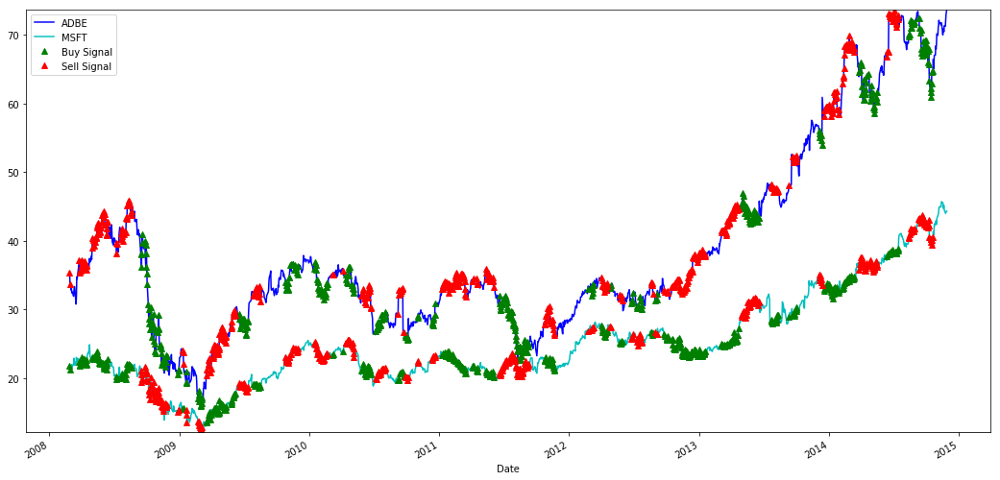
Signale zum Kaufen und Verkaufen von MSFT- und ADBE-Aktien

Beachten Sie, dass wir manchmal auf der „kurzen Seite“, manchmal auf der „langen Seite“ und manchmal auf beiden Seiten Geld verdienen.

Wir sind mit dem Signal der Trainingsdaten zufrieden. Mal sehen, welchen Gewinn dieses Signal generieren kann. Wir können einen einfachen Backtester erstellen, der 1 Verhältnis kauft (kauft 1 ADBE-Aktie und verkauft Verhältnis x MSFT-Aktie), wenn das Verhältnis niedrig ist, und 1 Verhältnis verkauft (verkauft 1 ADBE-Aktie und ruft Verhältnis x MSFT-Aktie auf) und berechnet die PnL-Trades für diese Verhältnisse.

# Trade using a simple strategy
def trade(S1, S2, window1, window2):
    
    # If window length is 0, algorithm doesn't make sense, so exit
    if (window1 == 0) or (window2 == 0):
        return 0
    
    # Compute rolling mean and rolling standard deviation
    ratios = S1/S2
    ma1 = ratios.rolling(window=window1,
                               center=False).mean()
    ma2 = ratios.rolling(window=window2,
                               center=False).mean()
    std = ratios.rolling(window=window2,
                        center=False).std()
    zscore = (ma1 - ma2)/std
    
    # Simulate trading
    # Start with no money and no positions
    money = 0
    countS1 = 0
    countS2 = 0
    for i in range(len(ratios)):
        # Sell short if the z-score is > 1
        if zscore[i] > 1:
            money += S1[i] - S2[i] * ratios[i]
            countS1 -= 1
            countS2 += ratios[i]
            print('Selling Ratio %s %s %s %s'%(money, ratios[i], countS1,countS2))
        # Buy long if the z-score is < 1
        elif zscore[i] < -1:
            money -= S1[i] - S2[i] * ratios[i]
            countS1 += 1
            countS2 -= ratios[i]
            print('Buying Ratio %s %s %s %s'%(money,ratios[i], countS1,countS2))
        # Clear positions if the z-score between -.5 and .5
        elif abs(zscore[i]) < 0.75:
            money += S1[i] * countS1 + S2[i] * countS2
            countS1 = 0
            countS2 = 0
            print('Exit pos %s %s %s %s'%(money,ratios[i], countS1,countS2))
            
            
    return money
trade(data['ADBE'].iloc[:1763], data['MSFT'].iloc[:1763], 60, 5)

Das Ergebnis ist: 1783.375

Diese Strategie scheint also profitabel zu sein! Jetzt können wir weitere Optimierungen vornehmen, indem wir das Zeitfenster für den gleitenden Durchschnitt ändern, die Schwellenwerte für Kauf-/Verkaufs- und Schließpositionen usw. ändern und die Leistungsverbesserungen anhand der Validierungsdaten überprüfen.

Wir können auch komplexere Modelle wie logistische Regression, SVM usw. für 1/-1-Vorhersagen ausprobieren.

Lassen Sie uns nun dieses Modell weiterentwickeln. Das führt uns zu

Schritt 7: Backtest der Testdaten

Hier möchte ich die Inventor Quantitative Platform erwähnen. Sie verwendet eine leistungsstarke QPS/TPS-Backtesting-Engine, um die historische Umgebung wirklichkeitsgetreu zu reproduzieren, gängige quantitative Backtesting-Fallen zu eliminieren und die Mängel der Strategie umgehend zu entdecken, um so bessere reale -Zeitaufwand. Bieten Sie Hilfe an.

Um das Prinzip zu erklären, wird in diesem Artikel die zugrundeliegende Logik dargestellt. In der praktischen Anwendung wird den Lesern empfohlen, die Inventor Quantitative Platform zu verwenden. Neben der Zeitersparnis ist es wichtig, die Fehlertoleranzrate zu verbessern.

Backtesting ist einfach. Wir können die obige Funktion verwenden, um den PnL der Testdaten anzuzeigen.

trade(data[‘ADBE’].iloc[1762:], data[‘MSFT’].iloc[1762:], 60, 5)

Das Ergebnis ist: 5262.868

Dieses Modell ist sehr gut gelungen! Es wurde unser erstes einfaches Paarhandelsmodell.

Vermeiden Sie Überanpassung

Bevor ich zum Schluss komme, möchte ich speziell über Überanpassung sprechen. Overfitting ist die gefährlichste Falle bei Handelsstrategien. Ein Overfitting-Algorithmus kann beim Backtesting zwar sehr gute Ergebnisse liefern, bei neuen, unbekannten Daten jedoch versagen. Dies bedeutet, dass er keine wirklichen Trends in den Daten aufdeckt und keine wirkliche Vorhersagekraft besitzt. Nehmen wir ein einfaches Beispiel.

In unserem Modell verwenden wir gleitende Parameterschätzungen und hoffen, die Länge des Zeitfensters zu optimieren. Wir könnten uns dazu entschließen, einfach alle Möglichkeiten und angemessenen Zeitfensterlängen zu durchlaufen und die Zeitdauer auszuwählen, auf deren Grundlage unser Modell die beste Leistung erbringt. Unten schreiben wir eine einfache Schleife, um die Zeitfensterlängen basierend auf dem PNL der Trainingsdaten zu bewerten und die beste Schleife zu finden.

# Find the window length 0-254 
# that gives the highest returns using this strategy
length_scores = [trade(data['ADBE'].iloc[:1762], 
                data['MSFT'].iloc[:1762], l, 5) 
                for l in range(255)]
best_length = np.argmax(length_scores)
print ('Best window length:', best_length)

('Best window length:', 40)

Jetzt überprüfen wir die Leistung des Modells anhand der Testdaten und sehen, dass diese Zeitfensterlänge alles andere als optimal ist! Dies liegt daran, dass unsere ursprüngliche Auswahl die Beispieldaten deutlich überanpasst.

# Find the returns for test data
# using what we think is the best window length
length_scores2 = [trade(data['ADBE'].iloc[1762:], 
                  data['MSFT'].iloc[1762:],l,5) 
                  for l in range(255)]
print (best_length, 'day window:', length_scores2[best_length])
# Find the best window length based on this dataset, 
# and the returns using this window length
best_length2 = np.argmax(length_scores2)
print (best_length2, 'day window:', length_scores2[best_length2])

(40, 'day window:', 1252233.1395)
(15, 'day window:', 1449116.4522)

Natürlich führt das, was für unsere Beispieldaten gut funktioniert, nicht unbedingt auch in der Zukunft zu guten Ergebnissen. Nur zum Testen zeichnen wir die aus den beiden Datensätzen berechneten Längenwerte auf

plt.figure(figsize=(15,7))
plt.plot(length_scores)
plt.plot(length_scores2)
plt.xlabel('Window length')
plt.ylabel('Score')
plt.legend(['Training', 'Test'])
plt.show()

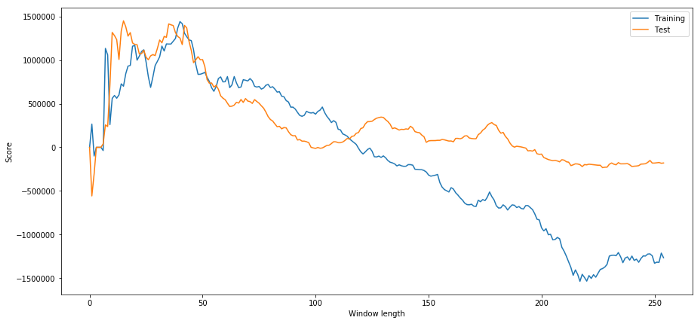
Wir können sehen, dass alles zwischen 20 und 50 eine gute Wahl für das Zeitfenster ist.

Um eine Überanpassung zu vermeiden, können wir bei der Wahl der Zeitfensterlänge ökonomische Überlegungen oder die Eigenschaften des Algorithmus nutzen. Wir können auch einen Kalman-Filter verwenden, bei dem wir keine Länge angeben müssen. Diese Methode wird später in einem anderen Artikel behandelt.

Nächster Schritt

In diesem Artikel stellen wir einige einfache Einführungsmethoden vor, um den Prozess der Entwicklung einer Handelsstrategie zu demonstrieren. In der Praxis sollten ausgefeiltere Statistiken verwendet werden. Sie können die folgenden Optionen in Betracht ziehen:

• Hurst-Exponent

• Die Halbwertszeit der Mittelwertumkehr, abgeleitet aus dem Ornstein-Uhlenbeck-Prozess

• Kalman-Filter