[TOC]

Rahmen des Faktormodells

Es gibt zahlreiche Forschungsberichte zum Multifaktormodell des Aktienmarktes mit umfassender Theorie und Praxis. Der Markt für digitale Währungen ist für die Faktorforschung ausreichend, unabhängig von der Anzahl der Währungen, dem Gesamtmarktwert, dem Transaktionsvolumen, dem Derivatemarkt usw. Dieser Artikel richtet sich hauptsächlich an Anfänger quantitativer Strategien und beinhaltet keine komplexen mathematischen Prinzipien und statistischen Analysen. Ausgehend vom Terminmarkt als Datenquelle wird ein einfacher Rahmen für die Faktorforschung erstellt, der die Auswertung der Faktorindikatoren erleichtern soll.

Ein Faktor kann als Indikator betrachtet und als Ausdruck geschrieben werden. Faktoren ändern sich kontinuierlich und spiegeln zukünftige Renditeinformationen wider. Normalerweise stellen Faktoren eine Anlagelogik dar.

Der Schlusskursfaktor beispielsweise basiert auf der Annahme, dass Aktienkurse zukünftige Renditen vorhersagen können. Je höher der Aktienkurs, desto höher die zukünftigen Renditen (oder desto niedriger die Renditen). Der Aufbau eines Portfolios auf der Grundlage dieses Faktors ist eigentlich eine Investition Modell/Strategie der regelmäßigen Positionsrotation zum Kauf hochpreisiger Aktien. . Im Allgemeinen werden Faktoren, die dauerhaft Überrenditen generieren können, oft als Alpha bezeichnet. So wurde beispielsweise von der Wissenschaft und der Investment-Community bestätigt, dass Marktkapitalisierungsfaktoren und Momentumfaktoren wirksame Faktoren sind.

Ob Aktienmarkt oder digitaler Währungsmarkt, es handelt sich um ein komplexes System. Kein Faktor kann zukünftige Renditen vollständig vorhersagen, aber es besteht dennoch ein gewisses Maß an Vorhersehbarkeit. Das effektive Alpha (Investitionsmodell) wird mit der Zeit unwirksam, je mehr Geld investiert wird. Dieser Prozess wird jedoch andere Modelle auf dem Markt hervorbringen und neue Alphas entstehen lassen. Der Marktkapitalisierungsfaktor war einst eine sehr effektive Strategie auf dem A-Aktienmarkt. Kaufen Sie einfach 10 Aktien mit der niedrigsten Marktkapitalisierung und passen Sie sie einmal täglich an. Der zehnjährige Backtest von 2007 wird mehr als das 400-fache der Rendite einbringen, weit den Gesamtmarkt übertreffend. . Allerdings spiegelte sich im Jahr 2017 am Blue-Chip-Aktienmarkt die Ineffektivität des Small-Market-Cap-Faktors wider, während stattdessen der Value-Faktor an Popularität gewann. Daher ist ein ständiges Abwägen und Experimentieren zwischen der Überprüfung und der Verwendung von Alpha erforderlich.

Die gesuchten Faktoren bilden die Grundlage für die Entwicklung von Strategien. Durch die Kombination mehrerer unabhängiger, wirksamer Faktoren können bessere Strategien entwickelt werden.

import requests
from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import requests, zipfile, io
%matplotlib inline

Datenquelle

Bis jetzt haben die stündlichen K-Line-Daten der Binance USDT Perpetual Futures von Anfang 2022 bis heute 150 Währungen überschritten. Wie bereits erwähnt, handelt es sich beim Faktormodell um ein Währungsauswahlmodell, das auf alle Währungen und nicht nur auf eine bestimmte Währung abzielt. Zu den K-Line-Daten zählen Daten wie hohe Eröffnungs- und niedrige Schlusskurse, Handelsvolumen, Anzahl der Transaktionen, aktives Kaufvolumen usw. Diese Daten sind sicherlich nicht die Quelle aller Faktoren, wie etwa des US-Aktienindex, der Zinserhöhungserwartungen , Rentabilität, On-Chain-Daten, Aufmerksamkeit in sozialen Medien usw. Weniger bekannte Datenquellen können möglicherweise ebenfalls ein effektives Alpha aufzeigen, grundlegende Volumen- und Preisdaten sind jedoch ebenfalls ausreichend.

## 当前交易对
Info = requests.get('https://fapi.binance.com/fapi/v1/exchangeInfo')
symbols = [s['symbol'] for s in Info.json()['symbols']]
symbols = list(filter(lambda x: x[-4:] == 'USDT', [s.split('_')[0] for s in symbols]))
print(symbols)

Out:

['BTCUSDT', 'ETHUSDT', 'BCHUSDT', 'XRPUSDT', 'EOSUSDT', 'LTCUSDT', 'TRXUSDT', 'ETCUSDT', 'LINKUSDT',
'XLMUSDT', 'ADAUSDT', 'XMRUSDT', 'DASHUSDT', 'ZECUSDT', 'XTZUSDT', 'BNBUSDT', 'ATOMUSDT', 'ONTUSDT',
'IOTAUSDT', 'BATUSDT', 'VETUSDT', 'NEOUSDT', 'QTUMUSDT', 'IOSTUSDT', 'THETAUSDT', 'ALGOUSDT', 'ZILUSDT',
'KNCUSDT', 'ZRXUSDT', 'COMPUSDT', 'OMGUSDT', 'DOGEUSDT', 'SXPUSDT', 'KAVAUSDT', 'BANDUSDT', 'RLCUSDT',
'WAVESUSDT', 'MKRUSDT', 'SNXUSDT', 'DOTUSDT', 'DEFIUSDT', 'YFIUSDT', 'BALUSDT', 'CRVUSDT', 'TRBUSDT',
'RUNEUSDT', 'SUSHIUSDT', 'SRMUSDT', 'EGLDUSDT', 'SOLUSDT', 'ICXUSDT', 'STORJUSDT', 'BLZUSDT', 'UNIUSDT',
'AVAXUSDT', 'FTMUSDT', 'HNTUSDT', 'ENJUSDT', 'FLMUSDT', 'TOMOUSDT', 'RENUSDT', 'KSMUSDT', 'NEARUSDT',
'AAVEUSDT', 'FILUSDT', 'RSRUSDT', 'LRCUSDT', 'MATICUSDT', 'OCEANUSDT', 'CVCUSDT', 'BELUSDT', 'CTKUSDT',
'AXSUSDT', 'ALPHAUSDT', 'ZENUSDT', 'SKLUSDT', 'GRTUSDT', '1INCHUSDT', 'CHZUSDT', 'SANDUSDT', 'ANKRUSDT',
'BTSUSDT', 'LITUSDT', 'UNFIUSDT', 'REEFUSDT', 'RVNUSDT', 'SFPUSDT', 'XEMUSDT', 'BTCSTUSDT', 'COTIUSDT',
'CHRUSDT', 'MANAUSDT', 'ALICEUSDT', 'HBARUSDT', 'ONEUSDT', 'LINAUSDT', 'STMXUSDT', 'DENTUSDT', 'CELRUSDT',
'HOTUSDT', 'MTLUSDT', 'OGNUSDT', 'NKNUSDT', 'SCUSDT', 'DGBUSDT', '1000SHIBUSDT', 'ICPUSDT', 'BAKEUSDT',
'GTCUSDT', 'BTCDOMUSDT', 'TLMUSDT', 'IOTXUSDT', 'AUDIOUSDT', 'RAYUSDT', 'C98USDT', 'MASKUSDT', 'ATAUSDT',
'DYDXUSDT', '1000XECUSDT', 'GALAUSDT', 'CELOUSDT', 'ARUSDT', 'KLAYUSDT', 'ARPAUSDT', 'CTSIUSDT', 'LPTUSDT',
'ENSUSDT', 'PEOPLEUSDT', 'ANTUSDT', 'ROSEUSDT', 'DUSKUSDT', 'FLOWUSDT', 'IMXUSDT', 'API3USDT', 'GMTUSDT',
'APEUSDT', 'BNXUSDT', 'WOOUSDT', 'FTTUSDT', 'JASMYUSDT', 'DARUSDT', 'GALUSDT', 'OPUSDT', 'BTCUSDT',
'ETHUSDT', 'INJUSDT', 'STGUSDT', 'FOOTBALLUSDT', 'SPELLUSDT', '1000LUNCUSDT', 'LUNA2USDT', 'LDOUSDT',
'CVXUSDT']

---

print(len(symbols))

Out:

153

---

#获取任意周期K线的函数
def GetKlines(symbol='BTCUSDT',start='2020-8-10',end='2021-8-10',period='1h',base='fapi',v = 'v1'):
    Klines = []
    start_time = int(time.mktime(datetime.strptime(start, "%Y-%m-%d").timetuple()))*1000 + 8*60*60*1000
    end_time =  min(int(time.mktime(datetime.strptime(end, "%Y-%m-%d").timetuple()))*1000 + 8*60*60*1000,time.time()*1000)
    intervel_map = {'m':60*1000,'h':60*60*1000,'d':24*60*60*1000}
    while start_time < end_time:
        mid_time = start_time+1000*int(period[:-1])*intervel_map[period[-1]]
        url = 'https://'+base+'.binance.com/'+base+'/'+v+'/klines?symbol=%s&interval=%s&startTime=%s&endTime=%s&limit=1000'%(symbol,period,start_time,mid_time)
        res = requests.get(url)
        res_list = res.json()
        if type(res_list) == list and len(res_list) > 0:
            start_time = res_list[-1][0]+int(period[:-1])*intervel_map[period[-1]]
            Klines += res_list
        if type(res_list) == list and len(res_list) == 0:
            start_time = start_time+1000*int(period[:-1])*intervel_map[period[-1]]
        if mid_time >= end_time:
            break
    df = pd.DataFrame(Klines,columns=['time','open','high','low','close','amount','end_time','volume','count','buy_amount','buy_volume','null']).astype('float')
    df.index = pd.to_datetime(df.time,unit='ms')
    return df

start_date = '2022-1-1'
end_date = '2022-09-14'
period = '1h'
df_dict = {}
for symbol in symbols:
    df_s = GetKlines(symbol=symbol,start=start_date,end=end_date,period=period,base='fapi',v='v1')
    if not df_s.empty:
        df_dict[symbol] = df_s

symbols = list(df_dict.keys())
print(df_s.columns)

Out:

Index(['time', 'open', 'high', 'low', 'close', 'amount', 'end_time', 'volume',
       'count', 'buy_amount', 'buy_volume', 'null'],
      dtype='object')

---

Wir extrahieren zunächst die interessierenden Daten aus den K-Linien-Daten: Schlusskurs, Eröffnungskurs, Handelsvolumen, Anzahl der Transaktionen und aktive Kaufquote und verwenden diese Daten als Grundlage für die Verarbeitung der erforderlichen Faktoren.

df_close = pd.DataFrame(index=pd.date_range(start=start_date, end=end_date, freq=period),columns=df_dict.keys())
df_open = pd.DataFrame(index=pd.date_range(start=start_date, end=end_date, freq=period),columns=df_dict.keys())
df_volume = pd.DataFrame(index=pd.date_range(start=start_date, end=end_date, freq=period),columns=df_dict.keys())
df_buy_ratio = pd.DataFrame(index=pd.date_range(start=start_date, end=end_date, freq=period),columns=df_dict.keys())
df_count = pd.DataFrame(index=pd.date_range(start=start_date, end=end_date, freq=period),columns=df_dict.keys())
for symbol in df_dict.keys():
    df_s = df_dict[symbol]
    df_close[symbol] = df_s.close
    df_open[symbol] = df_s.open
    df_volume[symbol] = df_s.volume
    df_count[symbol] = df_s['count']
    df_buy_ratio[symbol] = df_s.buy_amount/df_s.amount
df_close = df_close.dropna(how='all')
df_open = df_open.dropna(how='all')
df_volume = df_volume.dropna(how='all')
df_count = df_count.dropna(how='all')
df_buy_ratio = df_buy_ratio.dropna(how='all')

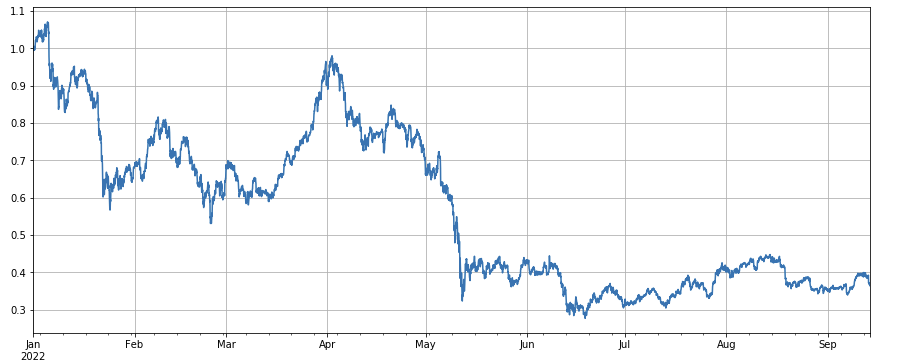
Betrachtet man die Entwicklung des Marktindex, so kann man sagen, dass er ziemlich düster ist. Er verzeichnete seit Jahresbeginn einen Rückgang von 60 %.

df_norm = df_close/df_close.fillna(method='bfill').iloc[0] #归一化
df_norm.mean(axis=1).plot(figsize=(15,6),grid=True);
#最终指数收益图

Bestimmung der Faktorvalidität

• Regressionsmethode Als abhängige Variable wird die Rendite der nächsten Periode verwendet, als unabhängige Variable der zu testende Faktor und der durch die Regression ermittelte Koeffizient ist die Rendite des Faktors. Nach dem Erstellen der Regressionsgleichung beziehen wir uns normalerweise auf den absoluten Mittelwert des Koeffizienten t-Werts, den Anteil der absoluten Wertfolge des Koeffizienten t-Werts größer als 2, die annualisierte Faktorrendite, die annualisierte Faktorrenditevolatilität, das Sharpe-Verhältnis von die Faktorrendite und andere Parameter. Faktoreffektivität und Volatilität. Sie können mehrere Faktoren gleichzeitig regressieren. Weitere Informationen finden Sie in der Barra-Dokumentation.

• IC, IR und andere Indikatoren Der sogenannte IC ist der Korrelationskoeffizient zwischen dem Faktor und der Rendite der nächsten Periode. Heutzutage wird im Allgemeinen RANK_IC verwendet, also der Korrelationskoeffizient zwischen der Faktorrangfolge und der Aktienrendite der nächsten Periode. IR ist im Allgemeinen der Mittelwert der IC-Sequenz/die Standardabweichung der IC-Sequenz.

• Hierarchische Regression In diesem Artikel wird diese Methode verwendet. Dabei werden die zu testenden Faktoren sortiert, die Währungen für das Gruppen-Backtesting in N Gruppen unterteilt und zum Anpassen der Positionen ein fester Zeitraum verwendet. Im Idealfall weisen die Renditen von N Währungsgruppen eine gute Monotonie auf, d. h. sie steigen oder fallen monoton, und die Renditelücke zwischen den einzelnen Gruppen ist groß. Solche Faktoren spiegeln sich in einer besseren Unterscheidung wider. Wenn die erste Gruppe die höchste Rendite und die letzte Gruppe die niedrigste Rendite hat, dann gehen Sie in der ersten Gruppe long und in der letzten Gruppe short. Die endgültige Rendite ist ein Referenzindikator für die Sharpe-Ratio.

Tatsächlicher Backtesting-Vorgang

Nach den Faktoren werden die ausgewählten Währungen in 3 Gruppen unterteilt, je nach Sortierung von klein nach groß. Jede Währungsgruppe macht etwa ¹⁄₃ aus. Wenn ein Faktor wirksam ist, gilt: Je kleiner der Anteil jeder Gruppe, desto höher ist der Rendite, aber es bedeutet auch, dass die jeder Währung zugewiesenen Mittel relativ groß sind. Wenn die Long- und Short-Positionen jeweils 1x gehebelt sind und die erste und letzte Gruppe jeweils 10 Währungen sind, dann machen sie jeweils 10 % aus. Wenn eine Währung, die Bei Short-Positionen beträgt die Korrektur 20 %, wenn sich der Investitionsbetrag verdoppelt. Wenn die Anzahl der Gruppen 50 beträgt, beträgt die Korrektur 4 %. Durch die Diversifizierung von Währungen kann das Risiko schwarzer Schwäne verringert werden. Gehen Sie bei der ersten Gruppe (mit dem kleinsten Faktorwert) long und bei der dritten Gruppe short. Wenn die Rendite umso höher ist, je größer der Faktor ist, können Sie die Long- und Short-Positionen umkehren oder den Faktor einfach negativ oder invers machen.

Die Vorhersagekraft eines Faktors lässt sich üblicherweise grob anhand der endgültigen Backtestrendite und der Sharpe-Ratio beurteilen. Darüber hinaus muss auch darauf Bezug genommen werden, ob der Faktorausdruck einfach ist, unempfindlich gegenüber der Größe der Gruppierung, unempfindlich gegenüber dem Positionsanpassungsintervall, unempfindlich gegenüber dem Anfangszeitpunkt des Backtests usw.

In Bezug auf die Häufigkeit der Positionsanpassung hat der Aktienmarkt oft einen Zyklus von 5 Tagen, 10 Tagen und einem Monat, aber für den digitalen Währungsmarkt ist ein solcher Zyklus zweifellos zu lang, und die Marktbedingungen auf dem realen Markt werden überwacht in in Echtzeit, daher ist es schwierig, einen bestimmten Zyklus einzuhalten. Es besteht keine Notwendigkeit, die Positionen erneut anzupassen, daher passen wir im realen Handel die Positionen in Echtzeit oder in kurzen Zeiträumen an.

Was das Schließen einer Position betrifft, können Sie die Position gemäß der herkömmlichen Methode schließen, wenn sie bei der nächsten Sortierung nicht in der Gruppe ist. Bei einer Positionsanpassung in Echtzeit können sich jedoch einige Währungen an der Trennlinie befinden und Positionen können hin und her geschlossen werden. Daher verfolgt diese Strategie den Ansatz, auf Gruppierungsänderungen zu warten und Positionen zu schließen, wenn es notwendig ist, Positionen in die entgegengesetzte Richtung zu öffnen. Wenn Sie beispielsweise in der ersten Gruppe long gehen, wenn die Währung in der Long-Position in die Dritte Gruppe: Sie können die Position schließen und einen Short gehen. Wenn Sie Positionen in einem festgelegten Zeitraum schließen, beispielsweise täglich oder alle 8 Stunden, können Sie die Positionen auch schließen, ohne zu einer Gruppe zu gehören. Sie können mehr versuchen.

#回测引擎
class Exchange:
    
    def __init__(self, trade_symbols, fee=0.0004, initial_balance=10000):
        self.initial_balance = initial_balance #初始的资产
        self.fee = fee
        self.trade_symbols = trade_symbols
        self.account = {'USDT':{'realised_profit':0, 'unrealised_profit':0, 'total':initial_balance, 'fee':0, 'leverage':0, 'hold':0}}
        for symbol in trade_symbols:
            self.account[symbol] = {'amount':0, 'hold_price':0, 'value':0, 'price':0, 'realised_profit':0,'unrealised_profit':0,'fee':0}
            
    def Trade(self, symbol, direction, price, amount):
        
        cover_amount = 0 if direction*self.account[symbol]['amount'] >=0 else min(abs(self.account[symbol]['amount']), amount)
        open_amount = amount - cover_amount
        self.account['USDT']['realised_profit'] -= price*amount*self.fee #扣除手续费
        self.account['USDT']['fee'] += price*amount*self.fee
        self.account[symbol]['fee'] += price*amount*self.fee

        if cover_amount > 0: #先平仓
            self.account['USDT']['realised_profit'] += -direction*(price - self.account[symbol]['hold_price'])*cover_amount  #利润
            self.account[symbol]['realised_profit'] += -direction*(price - self.account[symbol]['hold_price'])*cover_amount
            
            self.account[symbol]['amount'] -= -direction*cover_amount
            self.account[symbol]['hold_price'] = 0 if self.account[symbol]['amount'] == 0 else self.account[symbol]['hold_price']
            
        if open_amount > 0:
            total_cost = self.account[symbol]['hold_price']*direction*self.account[symbol]['amount'] + price*open_amount
            total_amount = direction*self.account[symbol]['amount']+open_amount
            
            self.account[symbol]['hold_price'] = total_cost/total_amount
            self.account[symbol]['amount'] += direction*open_amount
                    
    
    def Buy(self, symbol, price, amount):
        self.Trade(symbol, 1, price, amount)
        
    def Sell(self, symbol, price, amount):
        self.Trade(symbol, -1, price, amount)
        
    def Update(self, close_price): #对资产进行更新
        self.account['USDT']['unrealised_profit'] = 0
        self.account['USDT']['hold'] = 0
        for symbol in self.trade_symbols:
            if not np.isnan(close_price[symbol]):
                self.account[symbol]['unrealised_profit'] = (close_price[symbol] - self.account[symbol]['hold_price'])*self.account[symbol]['amount']
                self.account[symbol]['price'] = close_price[symbol]
                self.account[symbol]['value'] = abs(self.account[symbol]['amount'])*close_price[symbol]
                self.account['USDT']['hold'] += self.account[symbol]['value']
                self.account['USDT']['unrealised_profit'] += self.account[symbol]['unrealised_profit']
        self.account['USDT']['total'] = round(self.account['USDT']['realised_profit'] + self.initial_balance + self.account['USDT']['unrealised_profit'],6)
        self.account['USDT']['leverage'] = round(self.account['USDT']['hold']/self.account['USDT']['total'],3)

#测试因子的函数
def Test(factor, symbols, period=1, N=40, value=300):
    e = Exchange(symbols, fee=0.0002, initial_balance=10000)
    res_list = []
    index_list = []
    factor = factor.dropna(how='all')
    for idx, row in factor.iterrows():
        if idx.hour % period == 0:
            buy_symbols =  row.sort_values().dropna()[0:N].index
            sell_symbols = row.sort_values().dropna()[-N:].index
            prices = df_close.loc[idx,]
            index_list.append(idx)
            for symbol in symbols:
                if symbol in buy_symbols and e.account[symbol]['amount'] <= 0:
                    e.Buy(symbol,prices[symbol],value/prices[symbol]-e.account[symbol]['amount'])
                if symbol in sell_symbols and e.account[symbol]['amount'] >= 0:
                    e.Sell(symbol,prices[symbol], value/prices[symbol]+e.account[symbol]['amount'])
            e.Update(prices)
            res_list.append([e.account['USDT']['total'],e.account['USDT']['hold']])
    return pd.DataFrame(data=res_list, columns=['total','hold'],index = index_list)

Einfacher Faktorentest

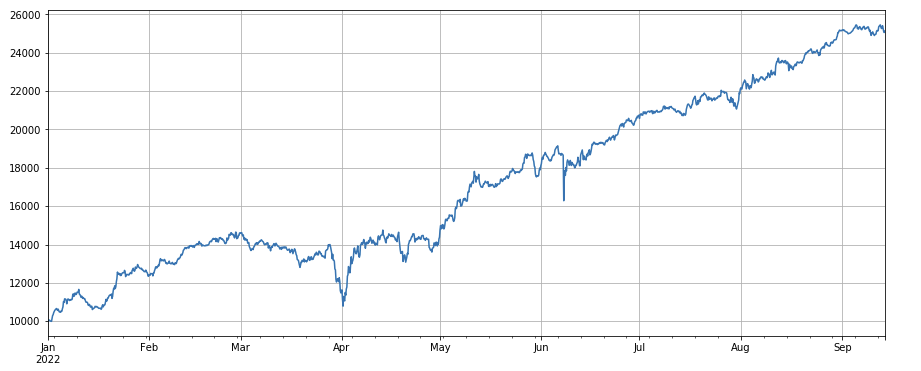
Volumenfaktor: Einfache Long-Positionen bei Münzen mit geringem Volumen und Short-Positionen bei Münzen mit hohem Volumen funktionieren sehr gut, was zeigt, dass beliebte Münzen eher fallen.

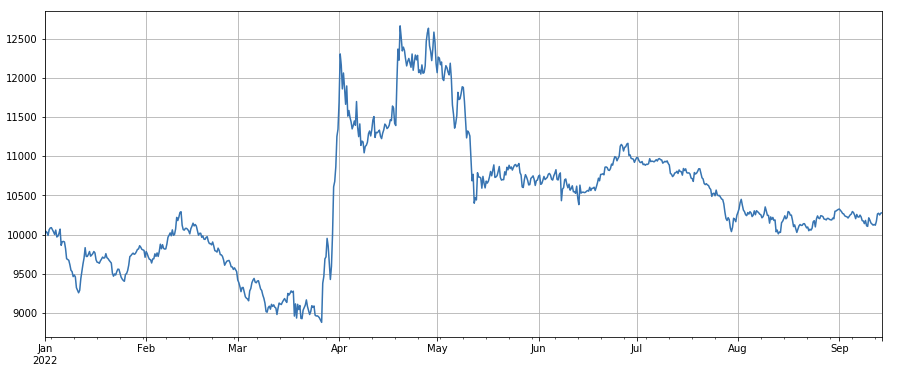
Transaktionspreisfaktor: Long-Position in niedrigpreisigen Währungen, Short-Position in hochpreisigen Währungen, der Effekt ist durchschnittlich.

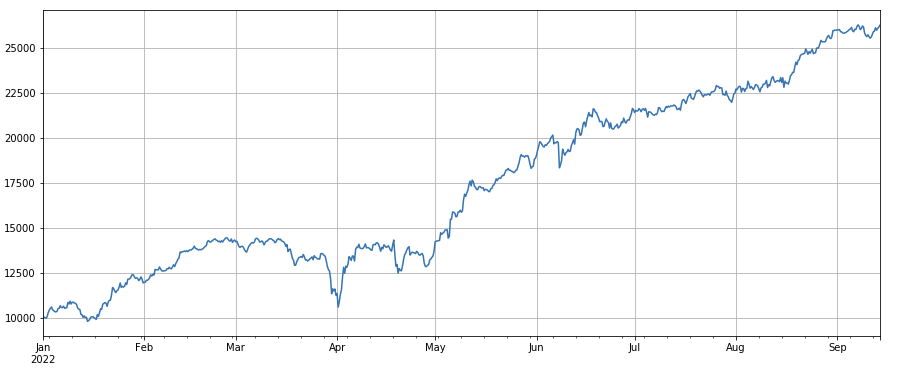
Faktor Anzahl der Transaktionen: Die Performance ist dem Volumen sehr ähnlich. Es ist offensichtlich, dass die Korrelation zwischen dem Volumenfaktor und dem Faktor Anzahl der Transaktionen sehr hoch ist. Tatsächlich beträgt die durchschnittliche Korrelation zwischen verschiedenen Währungen 0,97, was zeigt, dass diese beiden Faktoren sehr ähnlich sind. Dieser Faktor muss berücksichtigt werden .

3h Momentum-Faktor: (df_close - df_close.shift(3))/df_close.shift(3). Das heißt, der 3-Stunden-Anstieg des Faktors. Die Backtest-Ergebnisse zeigen, dass der 3-Stunden-Anstieg eine offensichtliche Regressionseigenschaft hat, d. h., der Anstieg wird in der nächsten Periode wahrscheinlicher fallen. Die Gesamtperformance ist gut, es gibt jedoch auch längere Phasen des Rückzugs und der Schwankungen.

24-Stunden-Momentum-Faktor: Die Ergebnisse des 24-Stunden-Neuausgleichszyklus sind ziemlich gut, mit Renditen ähnlich dem 3-Stunden-Momentum und einem geringeren Drawdown.

Umsatzänderungsfaktor: df_volume.rolling(24).mean() / df_volume.rolling(96).mean(), das ist das Verhältnis des Umsatzes des letzten Tages zum Umsatz der letzten drei Tage. Die Position wird alle 8 Stunden angepasst. Die Backtest-Ergebnisse sind relativ gut und das Retracement relativ niedrig, was zeigt, dass Aktien mit aktivem Handelsvolumen eher fallen.

Änderungsfaktor der Transaktionsnummer: df_count.rolling(24).mean() / df_count.rolling(96).mean(), das ist das Verhältnis der Anzahl der Transaktionen des letzten Tages zur Anzahl der Transaktionen der letzten drei Tage . Die Position wird alle 8 Stunden angepasst. . Die Backtest-Ergebnisse sind relativ gut und das Retracement relativ niedrig, was zeigt, dass der Markt mit zunehmender Anzahl von Transaktionen dazu neigt, aktiver zu fallen.

Faktor für die Wertänderung einzelner Transaktionen: -(df_volume.rolling(24).mean()/df_count.rolling(24).mean())/(df_volume.rolling(24).mean()/df_count.rolling(96).mean()) , das ist das Verhältnis des Transaktionswerts des letzten Tages zum Transaktionswert der letzten drei Tage, und die Position wird alle 8 Stunden angepasst. Auch dieser Faktor korreliert stark mit dem Volumenfaktor.

Faktor zur Änderung des aktiven Transaktionsverhältnisses: df_buy_ratio.rolling(24).mean()/df_buy_ratio.rolling(96).mean(), d. h. das Verhältnis des aktiven Kaufvolumens zum gesamten Transaktionsvolumen am letzten Tag vor der Transaktion Wert in den letzten drei Tagen, passen Sie die Position alle 8 Stunden an. Dieser Faktor weist eine gute Leistung auf und hat wenig Korrelation mit dem Volumenfaktor.

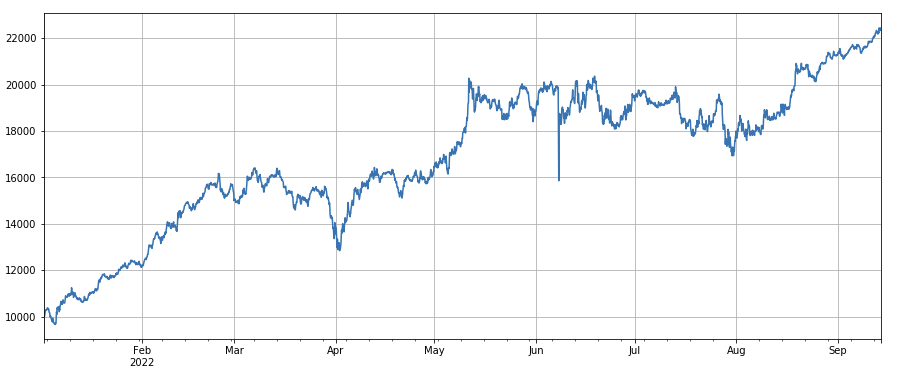
Volatilitätsfaktor: (df_close/df_open).rolling(24).std(), der einen bestimmten Effekt bei Long-Positionen in Währungen mit geringer Volatilität hat.

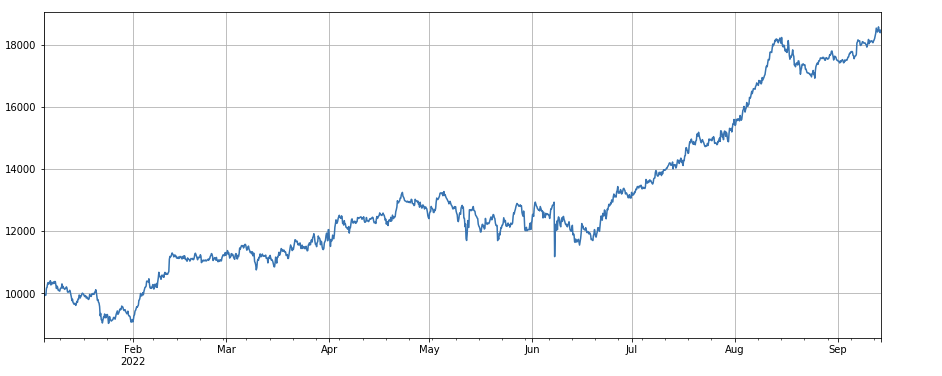
Korrelationsfaktor zwischen Handelsvolumen und Schlusskurs: df_close.rolling(96).corr(df_volume), der Korrelationsfaktor zwischen Schlusskurs und Handelsvolumen in den letzten 4 Tagen, die Gesamtperformance ist gut.

Hier sind nur einige der Faktoren aufgeführt, die auf Menge und Preis basieren. Tatsächlich kann die Kombination von Faktorformeln sehr komplex sein und hat möglicherweise keine offensichtliche Logik. Sie können auf die bekannte ALPHA101-Faktorkonstruktionsmethode verweisen: https://github.com/STHSF/alpha101.

#成交量
factor_volume = df_volume
factor_volume_res = Test(factor_volume, symbols, period=4)
factor_volume_res.total.plot(figsize=(15,6),grid=True);

#成交价
factor_close = df_close
factor_close_res = Test(factor_close, symbols, period=8)
factor_close_res.total.plot(figsize=(15,6),grid=True);

#成交笔数
factor_count = df_count
factor_count_res = Test(factor_count, symbols, period=8)
factor_count_res.total.plot(figsize=(15,6),grid=True);

print(df_count.corrwith(df_volume).mean())

0.9671246744996017

#3小时动量因子
factor_1 =  (df_close - df_close.shift(3))/df_close.shift(3)
factor_1_res = Test(factor_1,symbols,period=1)
factor_1_res.total.plot(figsize=(15,6),grid=True);

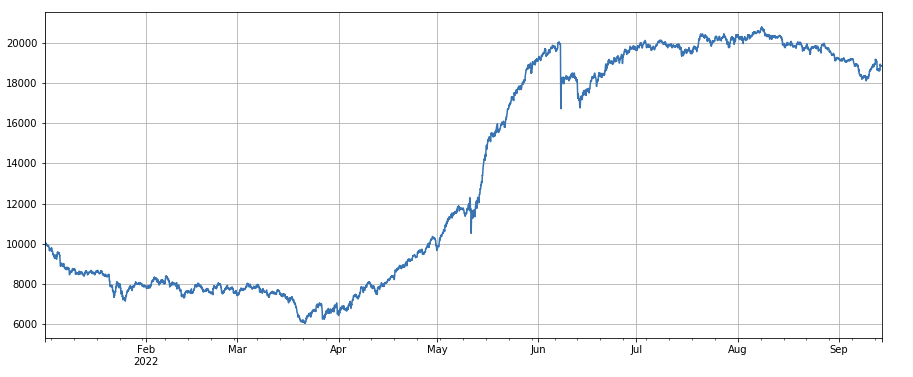
#24小时动量因子
factor_2 =  (df_close - df_close.shift(24))/df_close.shift(24)
factor_2_res = Test(factor_2,symbols,period=24)
tamenxuanfactor_2_res.total.plot(figsize=(15,6),grid=True);

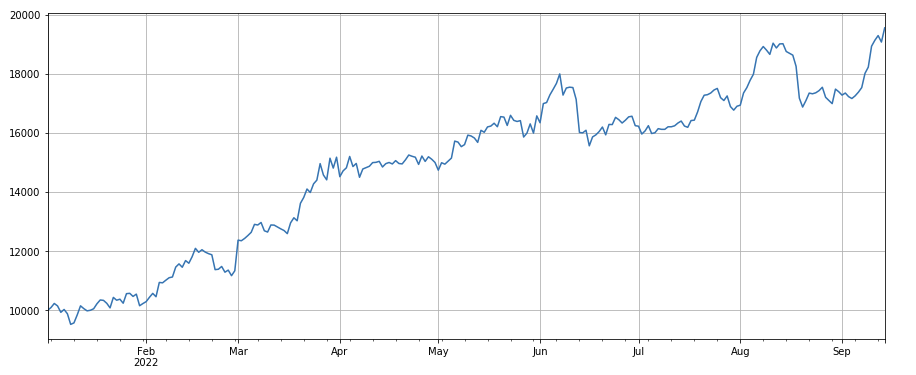
#成交量因子
factor_3 = df_volume.rolling(24).mean()/df_volume.rolling(96).mean()
factor_3_res = Test(factor_3, symbols, period=8)
factor_3_res.total.plot(figsize=(15,6),grid=True);

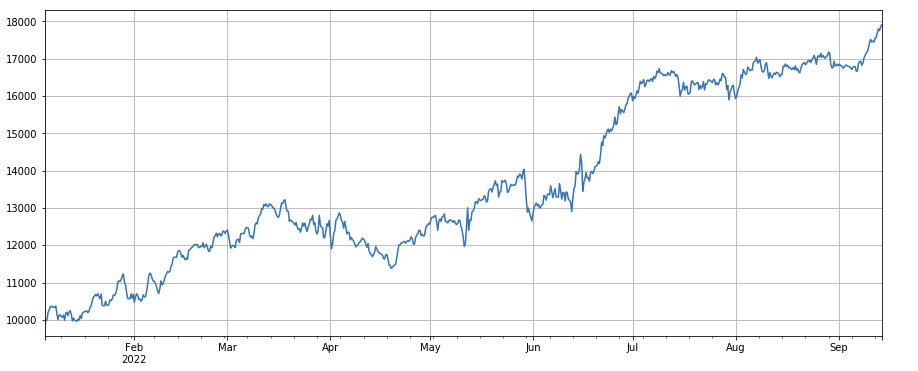
#成交笔数因子
factor_4 = df_count.rolling(24).mean()/df_count.rolling(96).mean()
factor_4_res = Test(factor_4, symbols, period=8)
factor_4_res.total.plot(figsize=(15,6),grid=True);

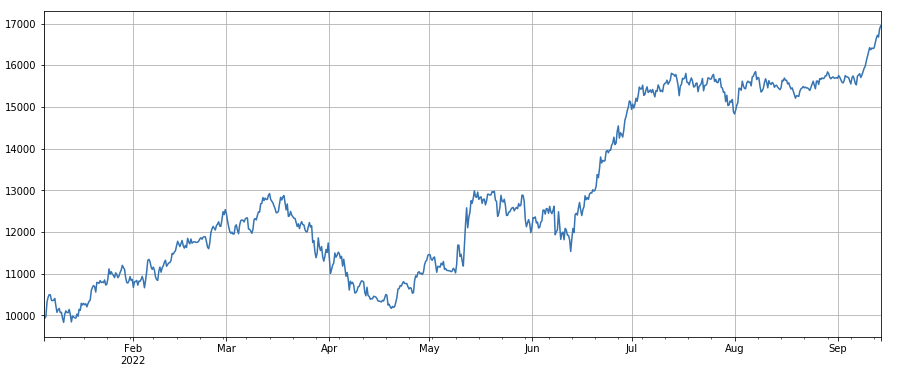
#因子相关性
print(factor_4.corrwith(factor_3).mean())

0.9707239580854841

#单笔成交价值因子
factor_5 = -(df_volume.rolling(24).mean()/df_count.rolling(24).mean())/(df_volume.rolling(24).mean()/df_count.rolling(96).mean())
factor_5_res = Test(factor_5, symbols, period=8)
factor_5_res.total.plot(figsize=(15,6),grid=True);

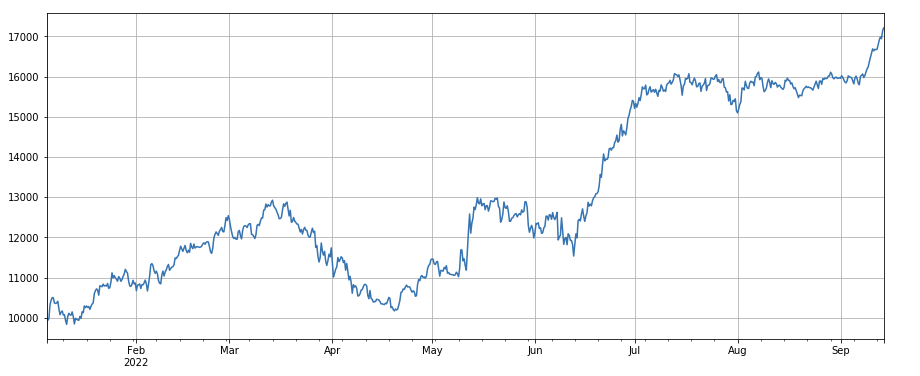
print(factor_4.corrwith(factor_5).mean())

0.861206620552479

#主动成交比例因子
factor_6 = df_buy_ratio.rolling(24).mean()/df_buy_ratio.rolling(96).mean()
factor_6_res = Test(factor_6, symbols, period=4)
factor_6_res.total.plot(figsize=(15,6),grid=True);

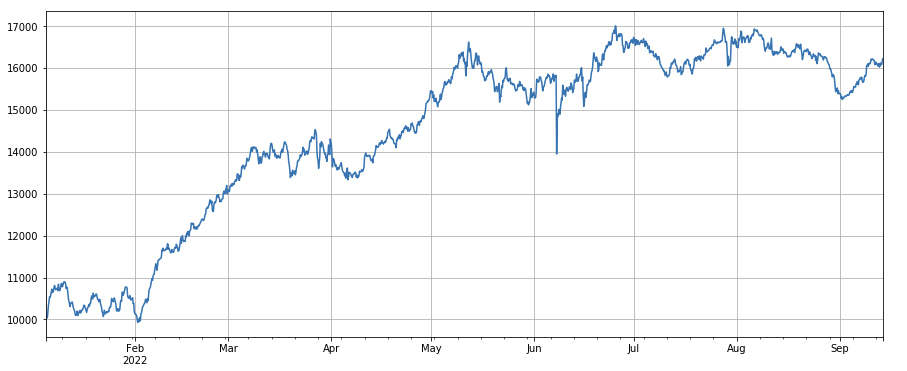
print(factor_3.corrwith(factor_6).mean())

0.1534572192503726

#波动率因子
factor_7 = (df_close/df_open).rolling(24).std()
factor_7_res = Test(factor_7, symbols, period=2)
factor_7_res.total.plot(figsize=(15,6),grid=True);

#成交量和收盘价相关性因子
factor_8 = df_close.rolling(96).corr(df_volume)
factor_8_res = Test(factor_8, symbols, period=4)
factor_8_res.total.plot(figsize=(15,6),grid=True);

Multifaktorsynthese

Das kontinuierliche Entdecken neuer wirksamer Faktoren ist sicherlich der wichtigste Teil des Strategieentwicklungsprozesses, doch ohne eine gute Methode zur Faktorsynthese kann ein einzelner hervorragender Alpha-Faktor seine volle Wirkung nicht entfalten. Zu den gängigen Methoden der Multifaktorsynthese gehören:

Methode der gleichen Gewichtung: Alle zu synthetisierenden Faktoren werden mit gleichen Gewichten addiert, um neue synthetisierte Faktoren zu erhalten.

Gewichtete Methode der historischen Faktorrenditen: Alle zu synthetisierenden Faktoren werden gemäß dem arithmetischen Mittel der historischen Faktorrenditen im aktuellsten Zeitraum als Gewichte addiert, um neue synthetisierte Faktoren zu erhalten. Bei dieser Methode wird den Faktoren, die gute Ergebnisse erzielen, ein höheres Gewicht beigemessen.

Maximierende IC_IR-Gewichtungsmethode: Der durchschnittliche IC-Wert des zusammengesetzten Faktors über einen historischen Zeitraum wird als Schätzung des IC-Werts des zusammengesetzten Faktors im nächsten Zeitraum verwendet, und die Kovarianzmatrix des historischen IC-Werts wird als Schätzung verwendet der Volatilität des zusammengesetzten Faktors im nächsten Zeitraum. Er entspricht dem erwarteten Wert von IC geteilt durch die Standardabweichung von IC, und die optimale Gewichtslösung zur Maximierung des zusammengesetzten Faktors IC_IR kann ermittelt werden.

Methode der Hauptkomponentenanalyse (PCA): PCA ist eine häufig verwendete Methode zur Reduzierung der Datendimensionalität. Die Korrelation zwischen Faktoren kann relativ hoch sein, und die Hauptkomponenten nach der Dimensionsreduzierung werden als synthetisierte Faktoren verwendet.

In diesem Artikel wird manuell auf die Faktorvaliditätsgewichtung Bezug genommen. Die oben beschriebene Methode kann sich beziehen auf:ae933a8c-5a94-4d92-8f33-d92b70c36119.pdf

Während beim Testen eines einzelnen Faktors die Reihenfolge festgelegt ist, erfordert die Multifaktorsynthese die Zusammenführung völlig unterschiedlicher Daten, sodass alle Faktoren standardisiert und im Allgemeinen Extremwerte und fehlende Werte entfernt werden müssen. Hier verwenden wir df_volume\factor_1\factor_7\factor_6\factor_8 für die Synthese.

#标准化函数，去除缺失值和极值，并且进行标准化处理
def norm_factor(factor):
    factor = factor.dropna(how='all')
    factor_clip = factor.apply(lambda x:x.clip(x.quantile(0.2), x.quantile(0.8)),axis=1)
    factor_norm = factor_clip.add(-factor_clip.mean(axis=1),axis ='index').div(factor_clip.std(axis=1),axis ='index')
    return factor_norm


df_volume_norm = norm_factor(df_volume)
factor_1_norm = norm_factor(factor_1)
factor_6_norm = norm_factor(factor_6)
factor_7_norm = norm_factor(factor_7)
factor_8_norm = norm_factor(factor_8)

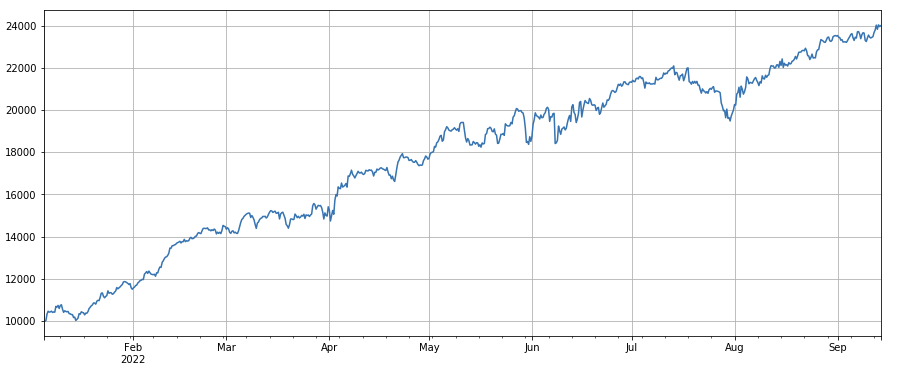
factor_total = 0.6*df_volume_norm + 0.4*factor_1_norm + 0.2*factor_6_norm + 0.3*factor_7_norm + 0.4*factor_8_norm
factor_total_res = Test(factor_total, symbols, period=8)
factor_total_res.total.plot(figsize=(15,6),grid=True);

Zusammenfassen

Dieser Artikel stellt die Einzelfaktor-Testmethode vor und testet die gemeinsamen Einzelfaktoren. Außerdem wird zunächst die Methode der Multifaktor-Synthese vorgestellt. Der Inhalt der Multifaktor-Forschung ist jedoch sehr umfangreich, und jeder im Artikel erwähnte Punkt kann erweitert werden. ausführlich. Es ist ein praktikabler Ansatz, solche Strategieforschung in die Entdeckung von Alpha-Faktoren umzuwandeln. Die Verwendung der Faktormethode kann die Überprüfung von Handelsideen erheblich beschleunigen, und es steht viel Referenzmaterial zur Verfügung.

Echte Adresse: https://www.fmz.com/robot/486605