Quantitative Strategie basierend auf dem Achsenabschnitt der linearen Regression

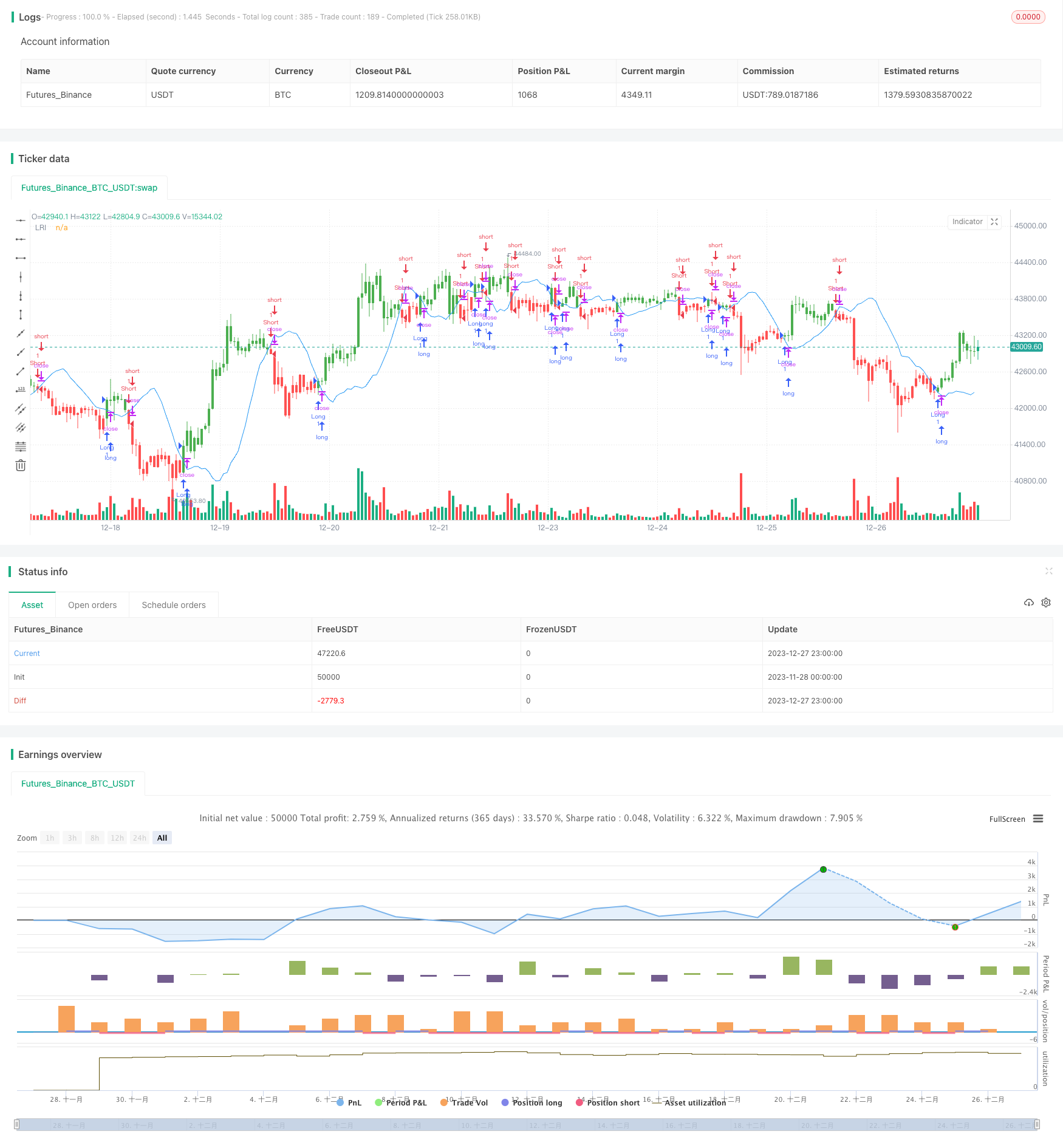
Überblick

Diese Strategie verwendet die Technik der linearen Regression, um die linearen Regressionsstopps zu berechnen und als Kauf- und Verkaufssignal zu verwenden, um eine quantitative Handelsstrategie zu erstellen. Die Strategie analysiert die Zeitreihen der Aktienpreise, stellt eine lineare Regressions-Trendlinie her und verwendet die linearen Regressionsstopps, um zu bestimmen, ob der Preis überschätzt oder unterbewertet ist, um einen Signalhandel zu erzeugen.

Strategieprinzip

Der lineare Regression-Blocking-Punkt ist der vorhergesagte Wert für den Y-Wert, wenn der Zeitreihenwert X 0 ist. Die Strategie setzt das Parameter Length vor, um den Schlusskurs als Quellsequenz zu verwenden, um den linearen Regression-Blocking-Punkt für den letzten Tag von Length zu berechnen.

Die Berechnungsformel lautet:

xX = Length *(Length - 1)* 0.5  
xDivisor = xX *xX - Length* Length *(Length - 1) *(2 * Length - 1) / 6
xXY = Σ(i *收盘价[i]),i从0到Length-1  
xSlope = (Length *xXY - xX* Σ(收盘价, Length))/ xDivisor
xLRI = (Σ(收盘价, Length) - xSlope * xX) / Length

Durch eine solche Berechnung kann man den Linear-Return-Interruptor xLRI des letzten Length-Tages erhalten. Die Strategie beurteilt die Preisentwicklung und erzeugt ein Handelssignal.

Strategische Vorteile

Diese Strategie hat folgende Vorteile:

1. Mit linearer Regression kann der Preis vorhergesagt und Trends ermittelt werden.
2. Weniger Parameter, einfaches Modell, leicht zu verstehen und umzusetzen.
3. Anpassbarer Parameter Length adaptive Flexibilität bei der Anpassung der Strategie.

Risiken und Lösungen

Die Strategie birgt auch Risiken:

1. Die lineare Regression-Anpassung ist lediglich eine statistische Anpassung, die auf historischen Daten basiert, und hat nur eine begrenzte Vorhersage über zukünftige Preisentwicklungen.
2. Die Ergebnisse der linearen Regressionsanpassung können widerrufen werden, wenn sich die Fundamentaldaten des Unternehmens stark verändern.
3. Die falsche Einstellung des Parameters “Length” kann zu einer Überpassung führen.

Gegenmaßnahmen:

1. Die Parameter “Length” werden entsprechend verkürzt, um eine Überpassung zu verhindern.
2. Das Unternehmen muss sich auf grundlegende Veränderungen konzentrieren, und wenn nötig, muss es seine Positionen schließen.
3. Die Anpassung der Parameter “Length” wird dynamisch an die Marktlage angepasst.

Richtung der Strategieoptimierung

Diese Strategie kann auch in folgenden Bereichen optimiert werden:

1. Erhöhung der Stop-Loss-Mechanismen, um einzelne Verluste zu kontrollieren.
2. In Kombination mit anderen Indikatoren, um eine kombinierte Strategie zu entwickeln und die Stabilität zu verbessern.
3. Die Parameter werden in den Optimierungsmodulen hinzugefügt, damit sich die Parameter von Length dynamisch ändern können.
4. Die Einführung eines Positionskontrollmoduls verhindert eine Überhöhung des Handels.

Zusammenfassen

Die Strategie basiert auf einem einfachen Quantifizierungs-Trading-Strategien basierend auf linearen Regressionsstopps. Insgesamt hat die Strategie einen gewissen wirtschaftlichen Wert, aber es gibt auch einige Risiken, die zu beachten sind. Durch kontinuierliche Optimierung wird erwartet, dass die Stabilität und Ertragsfähigkeit der Strategie weiter verbessert wird.