Adaptive gleitende Durchschnittsstrategie für Gaußsche Kanäle
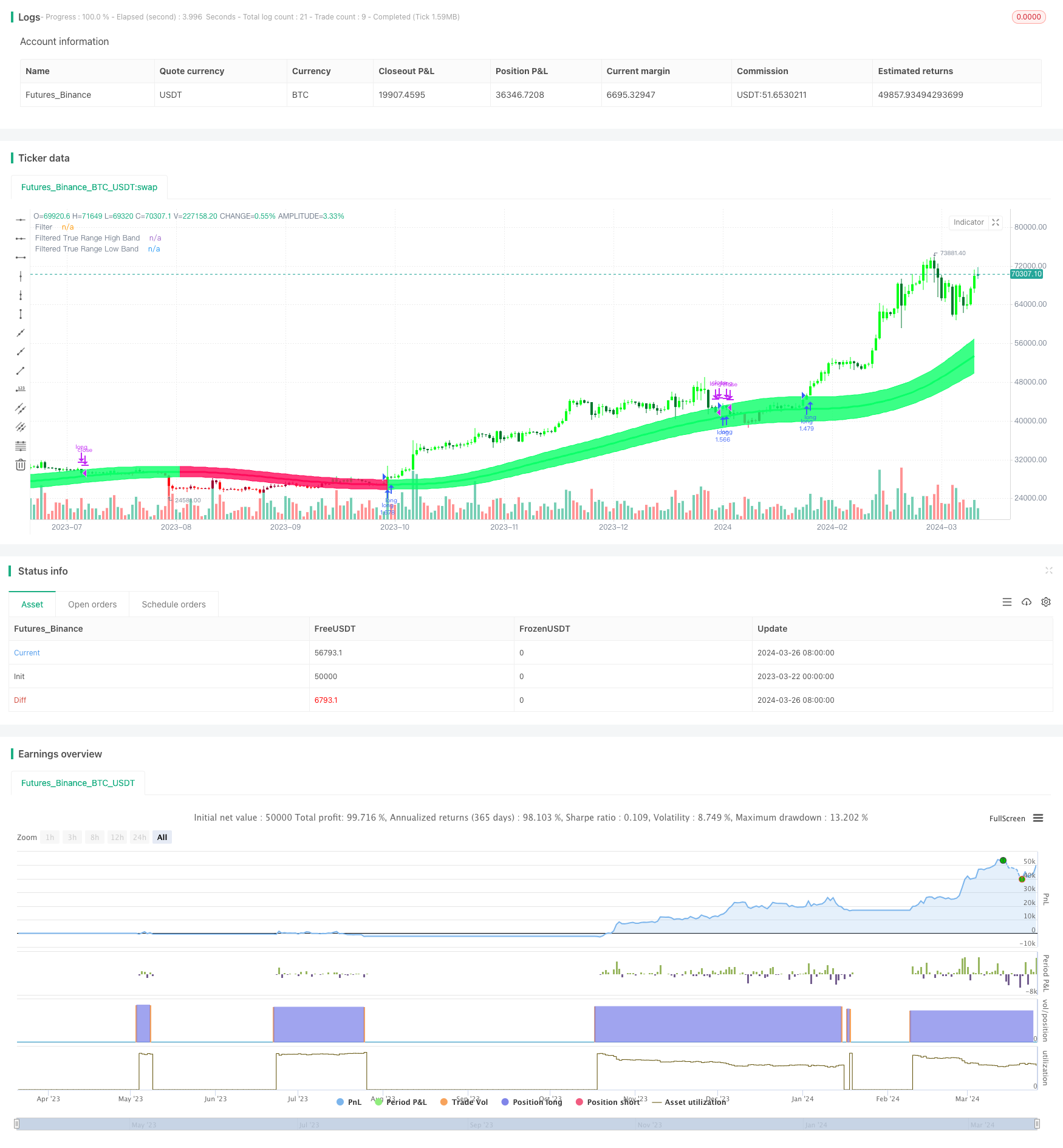
Überblick
Die Gauss-Kanal-Adaptive-Equilibrium-Strategie ist eine quantitative Handelsstrategie, die die Gauss-Schwanztechnik und die Adaptive-Parameter-Einstellungen nutzt. Die Strategie basiert auf der Gauss-Schwanz-Theorie von John Ehlers und erzeugt durch die Berechnung von mehrfachen Index-Moving Averages auf Preisdaten ein glattes und anpassungsfähiges Handelssignal.
Strategieprinzip
Das Prinzip der Anpassung der Gauss-Kanal-Einheitlichkeit lautet wie folgt:
- Berechnen Sie die Gauss-Wellenwerte des Preises. Berechnen Sie die Beta- und Alpha-Parameter nach dem vom Benutzer festgelegten Stichprobenzyklus und der Anzahl der Polarpunkte, und dann stufenweise Gauss-Wellen der Preisdaten, um eine glatte Preisfolge zu erhalten.
- Berechnen Sie den Gauss-Wellenwert der realen Schwankungsbreite. Die gleiche Gauss-Wellenbehandlung der realen Schwankungsbreite des Preises erfolgt, um eine glatte Schwankungsbreitenfolge zu erhalten.
- Bau eines Gauss-Kanals. Mit dem Preis nach der Gauss-Strahlung ist die mittlere Bahn, die oberste Bahn, die durch die mittlere Bahn addiert wird, die Multiplikation der tatsächlichen Schwankungsbreite mit der vom Benutzer eingestellten Multiplikation, die unterste Bahn, die durch die mittlere Bahn abgezogen wird, um einen dynamischen Kanal zu bilden.
- Erzeugt ein Handelssignal. Wenn der Preis nach oben durch die Kanalstraße geht, erzeugt er ein Kaufsignal. Wenn der Preis nach unten durch die Kanalstraße geht, erzeugt er ein Verkaufsignal.
- Einführung eines Zeitrahmenparameters. Der Benutzer kann die Start- und Endzeit der Strategie festlegen, in der die Strategie nach dem Handelssignal agiert.
Analyse der Stärken
Die Anpassung an die Gleichgewichtsstrategie des Goss-Kanals hat folgende Vorteile:
- Die Strategie verwendet dynamisch angepasste Parameter, die sich an verschiedene Marktbedingungen und Handelsarten anpassen können, ohne dass häufige manuelle Debugging erforderlich ist.
- Durch die Erstellung von Preiskanälen kann die Strategie die Markttrends besser erfassen und verfolgen und so falsche Signale in den schwindelerregenden Märkten effektiv vermeiden.
- Gute Glattigkeit. Die Verwendung von Goschenwellen-Technik zur mehrfachen Glatterung der Preisdaten entfernt den größten Teil des Marktrausches und macht die Handelssignale zuverlässiger.
- Hohe Flexibilität. Der Benutzer kann die Strategieparameter wie die Stichprobenperiode, die Polarität und die Schwankungsmenge anpassen, um die Strategie zu optimieren.
- Die Einführung von Zeitrahmenparametern ermöglicht die Ausführung von Strategien in einem bestimmten Zeitrahmen und erleichtert die Anwendung in der Praxis und die Rückmessung.
Risikoanalyse
Obwohl die Anpassungsstrategie des Grosskanals viele Vorteile hat, gibt es einige Risiken:
- Risiken bei der Einstellung von Parametern. Unpassende Einstellungen von Parametern können dazu führen, dass Strategien fehlschlagen oder schlecht funktionieren, was wiederholte Tests und Optimierungen in der Praxis erfordert.
- Das Risiko von Unvorhergesehenen. Bei einigen unvorhergesehenen Ereignissen kann es sein, dass die Strategie nicht rechtzeitig reagiert, was zu Verlusten führt.
- Überangemessenes Risiko. Wenn die Parameter zu gut auf die historischen Daten abgestimmt sind, kann dies dazu führen, dass die Strategie in der Zukunft schlechter funktioniert und die Leistung innerhalb und außerhalb der Stichprobe berücksichtigt werden muss.
- Die Strategie gilt hauptsächlich für trendige Märkte, wo es möglich ist, dass ein hohes Leverage-Risiko besteht, wenn Sie häufig in einem wackligen Markt handeln.
Optimierungsrichtung
Die Optimierung der Strategie von Gauss zur Anpassung an die Linie beinhaltet:
- Dynamische Parameteroptimierung. Durch die Einführung von Technologien wie maschinellem Lernen, um die automatische Optimierung und dynamische Anpassung der Strategieparameter zu ermöglichen, erhöht sich die Anpassungsfähigkeit.
- Multi-Faktor-Kombination: Die Kombination anderer effektiver technischer Indikatoren oder Faktoren mit dem Gauss-Kanal zur Bildung eines stabileren Handelssignals.
- Optimierung der Positionsverwaltung. Auf der Grundlage der Strategie werden vernünftige Regeln für die Positionsverwaltung und die Vermögensverwaltung aufgenommen, um Rücknahmen und Risiken zu kontrollieren.
- Multi-Variante-Synergie: Die Strategie wird auf mehrere verschiedene Handelsvarianten ausgeweitet, um das Risiko durch Asset-Planning und Relevanz-Analyse zu verteilen.
Zusammenfassen
Die Methode basiert auf der Dynamik von Gauss-Schwankungen und der Anpassung von Parametern, um durch die dynamische Konstruktion von Preiskanälen ein glattes und zuverlässiges Handelssignal zu erzeugen. Die Methode hat die Vorteile einer starken Anpassungsfähigkeit, einer guten Trendverfolgung, einer hohen Glattheit, einer hohen Flexibilität und einer hohen Praktikabilität, ist aber auch mit Risiken wie Parameter-Einstellung, Überschneidungen, Überanpassung und Scaling konfrontiert. Die Methode kann weiterentwickelt und verbessert werden.
/*backtest
start: 2023-03-22 00:00:00
end: 2024-03-27 00:00:00
period: 1d
basePeriod: 1h
exchanges: [{"eid":"Futures_Binance","currency":"BTC_USDT"}]
*/
//@version=4
strategy(title="Gaussian Channel Strategy v1.0", overlay=true, calc_on_every_tick=false, initial_capital=10000, default_qty_type=strategy.percent_of_equity, default_qty_value=100, commission_type=strategy.commission.percent, commission_value=0.1)
// Date condition inputs
startDate = input(title="Date Start", type=input.time, defval=timestamp("1 Jan 2018 00:00 +0000"), group="Dates")
endDate = input(title="Date End", type=input.time, defval=timestamp("31 Dec 2060 23:59 +0000"), group="Dates")
timeCondition = true
// This study is an experiment utilizing the Ehlers Gaussian Filter technique combined with lag reduction techniques and true range to analyze trend activity.
// Gaussian filters, as Ehlers explains it, are simply exponential moving averages applied multiple times.
// First, beta and alpha are calculated based on the sampling period and number of poles specified. The maximum number of poles available in this script is 9.
// Next, the data being analyzed is given a truncation option for reduced lag, which can be enabled with "Reduced Lag Mode".
// Then the alpha and source values are used to calculate the filter and filtered true range of the dataset.
// Filtered true range with a specified multiplier is then added to and subtracted from the filter, generating a channel.
// Lastly, a one pole filter with a N pole alpha is averaged with the filter to generate a faster filter, which can be enabled with "Fast Response Mode".
//Custom bar colors are included.
//Note: Both the sampling period and number of poles directly affect how much lag the indicator has, and how smooth the output is.
// Larger inputs will result in smoother outputs with increased lag, and smaller inputs will have noisier outputs with reduced lag.
// For the best results, I recommend not setting the sampling period any lower than the number of poles + 1. Going lower truncates the equation.
//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
//Updates:
// Huge shoutout to @e2e4mfck for taking the time to improve the calculation method!
// -> migrated to v4
// -> pi is now calculated using trig identities rather than being explicitly defined.
// -> The filter calculations are now organized into functions rather than being individually defined.
// -> Revamped color scheme.
//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
//Functions - courtesy of @e2e4mfck
//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
//Filter function
f_filt9x (_a, _s, _i) =>
int _m2 = 0, int _m3 = 0, int _m4 = 0, int _m5 = 0, int _m6 = 0,
int _m7 = 0, int _m8 = 0, int _m9 = 0, float _f = .0, _x = (1 - _a)
// Weights.
// Initial weight _m1 is a pole number and equal to _i
_m2 := _i == 9 ? 36 : _i == 8 ? 28 : _i == 7 ? 21 : _i == 6 ? 15 : _i == 5 ? 10 : _i == 4 ? 6 : _i == 3 ? 3 : _i == 2 ? 1 : 0
_m3 := _i == 9 ? 84 : _i == 8 ? 56 : _i == 7 ? 35 : _i == 6 ? 20 : _i == 5 ? 10 : _i == 4 ? 4 : _i == 3 ? 1 : 0
_m4 := _i == 9 ? 126 : _i == 8 ? 70 : _i == 7 ? 35 : _i == 6 ? 15 : _i == 5 ? 5 : _i == 4 ? 1 : 0
_m5 := _i == 9 ? 126 : _i == 8 ? 56 : _i == 7 ? 21 : _i == 6 ? 6 : _i == 5 ? 1 : 0
_m6 := _i == 9 ? 84 : _i == 8 ? 28 : _i == 7 ? 7 : _i == 6 ? 1 : 0
_m7 := _i == 9 ? 36 : _i == 8 ? 8 : _i == 7 ? 1 : 0
_m8 := _i == 9 ? 9 : _i == 8 ? 1 : 0
_m9 := _i == 9 ? 1 : 0
// filter
_f := pow(_a, _i) * nz(_s) +
_i * _x * nz(_f[1]) - (_i >= 2 ?
_m2 * pow(_x, 2) * nz(_f[2]) : 0) + (_i >= 3 ?
_m3 * pow(_x, 3) * nz(_f[3]) : 0) - (_i >= 4 ?
_m4 * pow(_x, 4) * nz(_f[4]) : 0) + (_i >= 5 ?
_m5 * pow(_x, 5) * nz(_f[5]) : 0) - (_i >= 6 ?
_m6 * pow(_x, 6) * nz(_f[6]) : 0) + (_i >= 7 ?
_m7 * pow(_x, 7) * nz(_f[7]) : 0) - (_i >= 8 ?
_m8 * pow(_x, 8) * nz(_f[8]) : 0) + (_i == 9 ?
_m9 * pow(_x, 9) * nz(_f[9]) : 0)
//9 var declaration fun
f_pole (_a, _s, _i) =>
_f1 = f_filt9x(_a, _s, 1), _f2 = (_i >= 2 ? f_filt9x(_a, _s, 2) : 0), _f3 = (_i >= 3 ? f_filt9x(_a, _s, 3) : 0)
_f4 = (_i >= 4 ? f_filt9x(_a, _s, 4) : 0), _f5 = (_i >= 5 ? f_filt9x(_a, _s, 5) : 0), _f6 = (_i >= 6 ? f_filt9x(_a, _s, 6) : 0)
_f7 = (_i >= 2 ? f_filt9x(_a, _s, 7) : 0), _f8 = (_i >= 8 ? f_filt9x(_a, _s, 8) : 0), _f9 = (_i == 9 ? f_filt9x(_a, _s, 9) : 0)
_fn = _i == 1 ? _f1 : _i == 2 ? _f2 : _i == 3 ? _f3 :
_i == 4 ? _f4 : _i == 5 ? _f5 : _i == 6 ? _f6 :
_i == 7 ? _f7 : _i == 8 ? _f8 : _i == 9 ? _f9 : na
[_fn, _f1]
//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
//Inputs
//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
//Source
src = input(defval=hlc3, title="Source")
//Poles
int N = input(defval=4, title="Poles", minval=1, maxval=9)
//Period
int per = input(defval=144, title="Sampling Period", minval=2)
//True Range Multiplier
float mult = input(defval=1.414, title="Filtered True Range Multiplier", minval=0)
//Lag Reduction
bool modeLag = input(defval=false, title="Reduced Lag Mode")
bool modeFast = input(defval=false, title="Fast Response Mode")
//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
//Definitions
//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
//Beta and Alpha Components
beta = (1 - cos(4*asin(1)/per)) / (pow(1.414, 2/N) - 1)
alpha = - beta + sqrt(pow(beta, 2) + 2*beta)
//Lag
lag = (per - 1)/(2*N)
//Data
srcdata = modeLag ? src + (src - src[lag]) : src
trdata = modeLag ? tr(true) + (tr(true) - tr(true)[lag]) : tr(true)
//Filtered Values
[filtn, filt1] = f_pole(alpha, srcdata, N)
[filtntr, filt1tr] = f_pole(alpha, trdata, N)
//Lag Reduction
filt = modeFast ? (filtn + filt1)/2 : filtn
filttr = modeFast ? (filtntr + filt1tr)/2 : filtntr
//Bands
hband = filt + filttr*mult
lband = filt - filttr*mult
// Colors
color1 = #0aff68
color2 = #00752d
color3 = #ff0a5a
color4 = #990032
fcolor = filt > filt[1] ? #0aff68 : filt < filt[1] ? #ff0a5a : #cccccc
barcolor = (src > src[1]) and (src > filt) and (src < hband) ? #0aff68 : (src > src[1]) and (src >= hband) ? #0aff1b : (src <= src[1]) and (src > filt) ? #00752d :
(src < src[1]) and (src < filt) and (src > lband) ? #ff0a5a : (src < src[1]) and (src <= lband) ? #ff0a11 : (src >= src[1]) and (src < filt) ? #990032 : #cccccc
//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
//Outputs
//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
//Filter Plot
filtplot = plot(filt, title="Filter", color=fcolor, linewidth=3)
//Band Plots
hbandplot = plot(hband, title="Filtered True Range High Band", color=fcolor)
lbandplot = plot(lband, title="Filtered True Range Low Band", color=fcolor)
//Channel Fill
fill(hbandplot, lbandplot, title="Channel Fill", color=fcolor, transp=80)
//Bar Color
barcolor(barcolor)
longCondition = crossover(close, hband) and timeCondition
closeAllCondition = crossunder(close, hband) and timeCondition
if longCondition
strategy.entry("long", strategy.long)
if closeAllCondition
strategy.close("long")