Black-Scholes-Strategie zur Volatilitätsanpassung bei dynamischem Ausbruch

Überblick

Die Black-Scholes-Strategie ist eine quantitative Handelsmethode, die auf der Theorie der Statistik und des Optionspreises basiert. Die Strategie wendet die Ideen des Black-Scholes-Modells geschickt auf die Analyse von Marktpreisbrechen an, um eine intelligente Erfassung von Brechungssignalen durch die Berechnung historischer Volatilität und die dynamische Anpassung der erwarteten Preisspanne zu ermöglichen.

Strategieprinzip

Die Strategie basiert auf folgenden Schritten:

1. Berechnung der Volatilität: Zuerst berechnen Sie die logarithmische Rendite der historischen Rendite (logReturn = math.log) (close / close)[1])), berechnen Sie dann die Standarddifferenz dieser Parameter-Renditen mit der festgelegten Rücklaufzeit (die Standarddifferenz ist 20 Zyklen) und annullieren Sie diese (die Standarddifferenz wird mit der Quadratwurzel des Handelszyklus multipliziert, wobei 252 Handelstage pro Jahr und 390 Minuten pro Tag berücksichtigt werden).

2. Berechnung der erwarteten Bewegung: Berechnung der erwarteten Preisbewegung für jede Handelsphase mit Hilfe der von Blake-Scholes inspirierten Methode[1] * volatility * math.sqrt ((1 / periodsPerYear)) . Das ist eigentlich die Umrechnung der jährlichen Volatilitätsrate in die erwartete Veränderung für einen einzelnen Zeitraum .

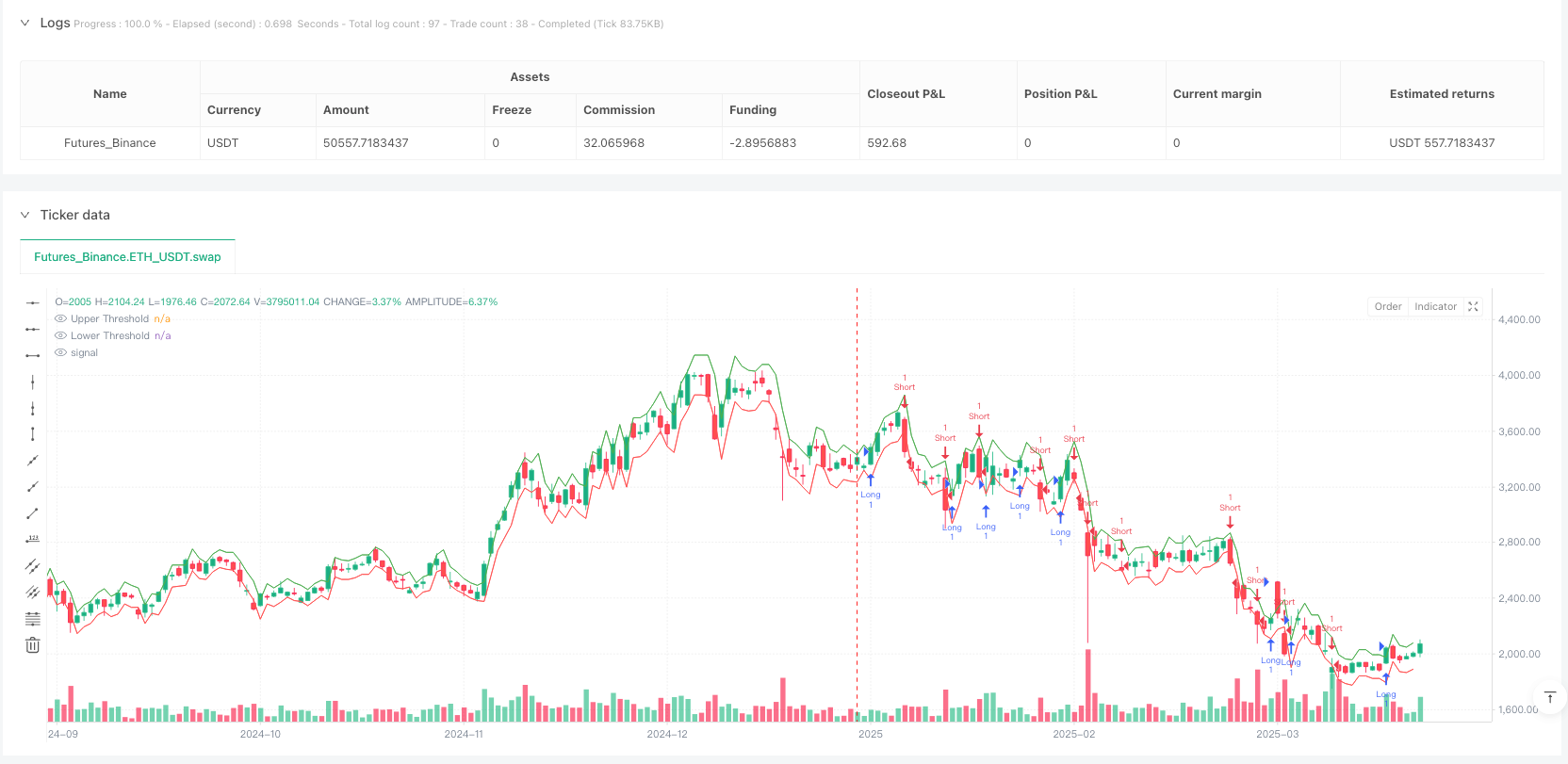
3. Dynamische Threshold-Einstellung: Setzen Sie die beiden nächsten Thresholds auf den vorherigen Schlusskurs und die berechnete erwartete Bewegung ((upperThreshold = close[1] + expectedMove und lowerThreshold = close[1] - expectedMove）。

4. Handelssignalgenerierung: Wenn der aktuelle Schlusskurs die Obergrenze überschreitet, wird ein Mehrsignal ausgelöst; wenn die Obergrenze überschritten wird, wird ein Kurzsignal ausgelöst.

5. Risikomanagement: Die Strategie setzt automatisch nach dem Eintritt in den Handel auf prozentuale Stop-Losses (Standard 1%) und Stop-Ops (Standard 2%). Bei Mehrfachpositionen wird der Stop-Loss auf einen bestimmten Prozentsatz unter dem Einstiegspreis und der Stop-Ops auf einen bestimmten Prozentsatz über dem Einstiegspreis gesetzt; bei Leerpositionen umgekehrt.

Analyse der Stärken

1. Dynamische Anpassungsfähigkeit: Im Vergleich zu traditionellen Breakout-Strategien, die einen festen Preis oder einen Prozentsatz verwenden, kann die Strategie die Breakout-Trenche dynamisch an die tatsächlichen Marktschwankungen anpassen und ist besser an unterschiedliche Marktbedingungen und schwankende Umgebungen angepasst.

2. Statistische Grundlagen: Die Strategie basiert auf bewährten statistischen Prinzipien und der Theorie der Optionspreisung, verwendet die logarithmische Rendite und die Berechnung der Standarddifferenz, die theoretische Grundlage ist solide.

3. Automatisches Risikomanagement: Die integrierte Stop-Loss- und Stop-Stop-Mechanismen sorgen dafür, dass für jeden Handel Risikokontrollen vorhanden sind, um eine übermäßige Haltung oder Verlustvergrößerung aufgrund von emotionalen Faktoren zu vermeiden.

4. Flexibilität der Parameter: Der Benutzer kann die Volatilitätsrücklauf-Zyklus, die Stop-Loss- und die Stop-Stop-Prozentsätze anpassen, um die Strategie anpassungsfähig zu machen, je nach Markt und persönlichen Risikopräferenzen.

5. Berechnungseffizienz: Die Berechnung der Strategie ist relativ einfach und unmittelbar, ohne komplexe Kombinationen von Indikatoren, wodurch das Risiko einer Überfusion verringert und die Effizienz der Ausführung erhöht wird.

Risikoanalyse

1. False-Breakout-Risiken: Es kann ein schneller Rückzug des Marktes nach einem kurzen Wertminderungsschub auftreten, was zu falschen Signalen und unnötigen Handelskosten führt. Dieses Risiko kann durch die Erhöhung der Bestätigungsmechanismen verringert werden (z. B. durch die Aufforderung, dass der Durchbruch eine bestimmte Zeit dauert oder eine Bestätigung der Handelsmenge kombiniert wird).

2. Schwankungsrate-Schätzungsfehler: Die historische Schwankungsrate ist nicht immer in der Lage, die zukünftige Schwankung genau vorherzusagen, insbesondere bei starken Veränderungen der Marktbedingungen. Es kann in Betracht gezogen werden, die Schwankungsrate in Verbindung mit der impliziten Schwankungsrate oder mit komplexeren Schwankungsrate-Modellen wie GARCH zu kombinieren, um die Prognose-Genauigkeit zu verbessern.

3. Parameter-Sensitivität: Die Strategie-Performance ist möglicherweise empfindlich auf die Volatilitätsrücklauf-Zyklen, die Stop-Loss- und Stop-Stop-Einstellungen. Es wird empfohlen, eine umfassende Rückmessung und Parameteroptimierung durchzuführen, um die optimale Kombination von Parametern für einen bestimmten Markt zu finden.

4. Trendmarktergebnis: In einem stark trendigen Markt kann es vorkommen, dass sich die Preise über die erwartete Schwankungsbreite hinaus in eine Richtung bewegen, was dazu führt, dass wichtige Trends verpasst werden. Eine Ergänzung der Strategie kann in Kombination mit einem Trendindikator in Betracht gezogen werden.

5. Auswirkungen auf die Transaktionskosten: Häufige Durchbruchsignale können zu viel Handel führen und die Kosten für Provisionen und Gleitpunkte erhöhen. Die Häufigkeit des Handels kann durch die Einrichtung von Handelsintervallen oder Signalfiltern verringert werden.

Optimierungsrichtung

1. Verbesserungen bei der Berechnung von Schwankungen: Die Berechnung von Schwankungen mit Hilfe des Index-Gewogenen Moving Averages (EWMA) oder des GARCH-Modells kann erforscht werden, um die Aggregationseffekte und die zeitlichen Eigenschaften von Schwankungen besser zu erfassen. Der Code für die Verbesserungen kann wie folgt sein:

// EWMA波动率计算
alpha = 0.94  // 衰减因子
ewmaVar = 0.0
ewmaVar := alpha * ewmaVar[1] + (1 - alpha) * logReturn * logReturn
ewmaVol = math.sqrt(ewmaVar) * math.sqrt(periodsPerYear)

1. Signal-Bestätigungsmechanismus: Hinzufügen von Mengenbestätigung oder Preisbewegung, um die Gefahr eines falschen Durchbruchs zu verringern:

volumeConfirmation = volume > ta.sma(volume, 20) * 1.5
momentumConfirmation = ta.rsi(close, 14) > 50 for longCondition or < 50 for shortCondition
longCondition := longCondition and volumeConfirmation and momentumConfirmation

1. Anpassungs-Stoppmechanismen: Dynamische Stopps basierend auf dem ATR, um besser auf Marktschwankungen zu reagieren:

atrPeriod = 14
atrMultiplier = 2
atrValue = ta.atr(atrPeriod)
dynamicStopLoss = atrMultiplier * atrValue

1. Zeitfilter: Hinzufügen von Zeitfiltern, um unregelmäßige Markteintritte und -abschlüsse zu vermeiden:

timeFilter = (hour >= 10 and hour < 15) or (hour == 15 and minute < 30)
longCondition := longCondition and timeFilter

1. Mehrzeitbestätigung: Filterung von Signalen, die sich gegen die Hauptrends richten, durch Überprüfung der Richtung in höheren Zeiträumen:

higherTimeframeClose = request.security(syminfo.tickerid, "60", close)
higherTimeframeTrend = ta.ema(higherTimeframeClose, 20) > ta.ema(higherTimeframeClose, 50)
longCondition := longCondition and higherTimeframeTrend
shortCondition := shortCondition and not higherTimeframeTrend

Zusammenfassen

Die Black-Scholes-Dynamic Breakout Strategie, die sich an der Volatilität anpasst, ist eine innovative quantitative Strategie, die die Optionspreistheorie mit traditionellen Methoden des Breakout-Tradings verbindet. Sie erstellt dynamische Handelsmargen, indem sie die Marktvolatilität berechnet und in den Bereich der erwarteten Preisänderung übertragen wird. Die Strategie passt sich effektiv an die Volatilität unter verschiedenen Marktbedingungen an.

Die Strategie sieht sich jedoch auch mit Herausforderungen konfrontiert, wie False Breaks, Schwankungsrate-Schätzungsfehler und Parameter-Sensitivität. Durch die Einführung von Optimierungsmaßnahmen wie Schwankungsrate-Berechnungsverbesserungen, Signalbestätigungsmechanismen, dynamische Risikomanagement und Multizyklus-Analyse kann die Stabilität und Zuverlässigkeit der Strategie erheblich verbessert werden. Diese Optimierungen helfen der Strategie, effektive Signale besser zu identifizieren und Risiken zu kontrollieren, insbesondere in einem hohen oder schnell wechselnden Marktumfeld.

Insgesamt stellt die Black-Scholes-Dynamic Breakthrough Strategie für die Volatilitätskorrektur einen effektiven Versuch dar, traditionelle technische Analyse mit moderner Finanztheorie zu kombinieren, um Quantitative Händlern einen Handelsprozess mit einer soliden theoretischen Grundlage, einer starken Flexibilität und einer einfachen Umsetzung zu bieten. Durch kontinuierliche Optimierung und angemessene Anpassung wird die Strategie unter verschiedenen Marktbedingungen eine solide Leistung erbringen.