AR-GARCH-Strategie zur Zeitreihenprognose
Warum funktioniert die traditionelle Tech-Analyse nicht in einem komplexen Markt?
In der Quantitative Trading-Branche werden wir oft mit der Frage konfrontiert, warum Strategien, die auf einfachen Moving Averages oder RSI basieren, in bestimmten Marktbedingungen hervorragend abschneiden, während sie in anderen Perioden häufig scheitern. Die Antwort liegt in der Komplexität der Finanzzeitreihen, die nicht nur von sich selbst korrelieren, sondern auch von den Schwankungen, die mit der Zeit einhergehen.
Die Strategie, die wir heute analysieren, kombiniert geschickt AR(2) Eigenregressionsmodelle und GARCH(1,1) Conditional Differential Modelle, um zu versuchen, das Problem aus statistischer Sicht zu lösen. Es handelt sich nicht um eine einfache Überschneidung technischer Kennzahlen, sondern um eine tiefgreifende Erforschung der wesentlichen Merkmale der Finanzzeitreihen.
Wie erfasst das Modell die Gedächtniswirkung von Preisen?
Der Kern der Strategie liegt in der Anwendung des AR(2) -Selbstregressionsmodells. Was ist Selbstregression? Einfach ausgedrückt, es ist die Vorhersage des zukünftigen Selbst anhand des vergangenen Selbst.
r_t = φ₁ × r_{t-1} + φ₂ × r_{t-2} + ε_t
Der Code enthält die Yule-Walker-Gleichung für die Koeffizienten φ1 und φ2:
c0 = calcAutoCovariance(returns, 0, lengthReg) // 滞后0期自协方差
c1 = calcAutoCovariance(returns, 1, lengthReg) // 滞后1期自协方差
c2 = calcAutoCovariance(returns, 2, lengthReg) // 滞后2期自协方差
phi1 = (c1 * c0 - c2 * c1) / denominator // 第一个自回归系数
phi2 = (c2 * c0 - c1 * c1) / denominator // 第二个自回归系数
Der Vorteil dieser Methode liegt darin, dass sie nicht auf subjektive Beurteilungen beruht, sondern die Daten selbst “sprechen” lässt und die Regelmäßigkeiten, die in der Preisreihenfolge enthalten sind, entdeckt.
Warum ist das GARCH-Modell besser geeignet, Marktrisiken abzubilden?
AR-Modelle allein reichen nicht aus, da die Volatilität der Finanzmärkte nicht konstant ist. Wir alle wissen, dass große Schwankungen oft mit großen Schwankungen einhergehen und Ruheperioden oft länger andauern.
Das GARCH ((1,1) Modell wurde entwickelt, um genau diese Eigenschaft zu veranschaulichen:
σ²_t = ω + α × ε²_{t-1} + β × σ²_{t-1}
Die Implementierungslogik des Codes zeigt dies deutlich:
omega = (1 - adjustedAlpha - adjustedBeta) * longTermVar
garchVariance := omega + adjustedAlpha * math.pow(arResidual[1], 2) + adjustedBeta * garchVariance[1]
Die wichtigste Erkenntnis ist, dass die gegenwärtige Konditionsdifferenz nicht nur vom Restdifferenz-Quadrat der vorherigen Periode abhängt (kurze Schläge), sondern auch von der Konditionsdifferenz der vorherigen Periode (langfristige Kontinuität). Die Parameter α steuern die Auswirkungen der kurzfristigen Schläge, β steuert die Kontinuität der Schwankungen.
Wie kann die Handelslogik der Strategie das Risiko-Gewinn-Verhältnis ausgleichen?
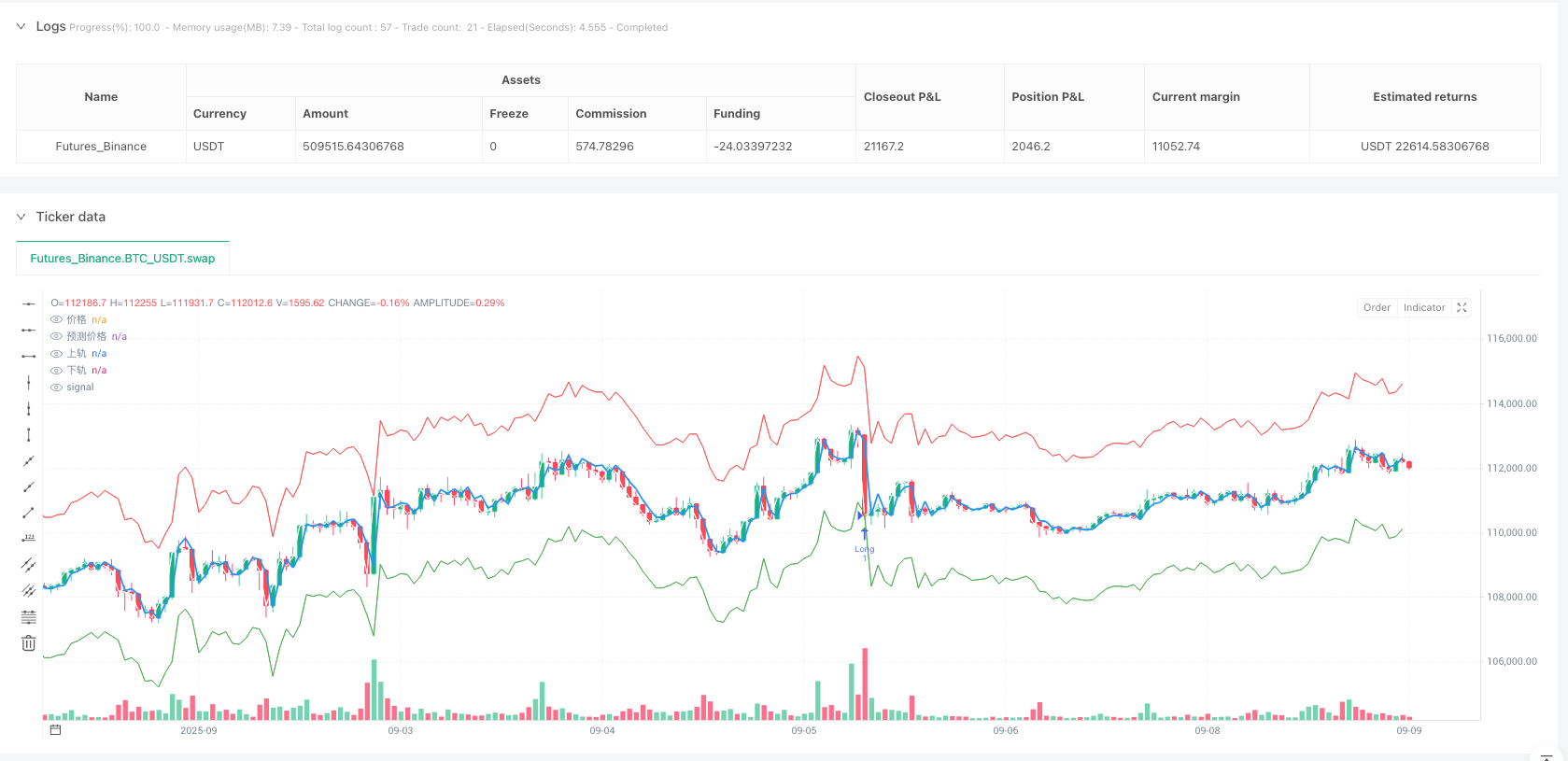
Mit AR-Vorhersagen und GARCH-Schwankungsrate-Schätzungen erstellt die Strategie einen dynamischen Konfidenzbereich:
upperReturnBand = arReturnPredict + stdevFactor * garchStd
lowerReturnBand = arReturnPredict - stdevFactor * garchStd
Die Logik der Erzeugung von Handelssignalen spiegelt die Idee der Mittelwertrückkehr wider:
- Wenn der Preis unterhalb der Bandbreite fällt, machen Sie mehr.
- Wenn der Preis in der oberen Bandbrechung ausfällt (shortSignal = rawPrice > upperPriceBand)
Die Kunst dieses Designs besteht darin, dass die Breite des Vertrauensbereichs sich dynamisch an die Marktfluktuation anpasst. In Zeiten hoher Volatilität wird der Bereich erweitert, was die Handelsfrequenz verringert; in Zeiten niedriger Volatilität wird der Bereich verengt, was die Handelsmöglichkeiten erhöht.
Welche Schlüsselfragen sind in der Praxis zu beachten?
1. Modellstabilitätsprüfung Der Code enthält wichtige Stabilitätsprüfungen:
if stabilityCheck >= 0.99 or math.abs(phi2) >= 0.99
scaleFactor = 0.95 / math.max(stabilityCheck, math.abs(phi2) + 0.01)
Dies gewährleistet die Gleichmäßigkeit der AR-Modelle und verhindert die Verteilung der Prognoseergebnisse.
2. Die Konvergenz der Parameter Das GARCH-Modell verlangt, dass α + β < 1 ist, um eine Langzeitdifferenz zu gewährleisten:
if sumParam >= 0.999
scale = 0.99 / sumParam
3. Die Notwendigkeit eines Filtermechanismus Die Strategie bietet RSI-Filteroptionen, die in praktischen Anwendungen wichtig sind. Rein statistische Modelle können tendenzielle Merkmale des Marktes ignorieren, und die Aufnahme von technischen Indikatoren kann zusätzliche Bestätigungssignale liefern.
Grenzen der Strategie und Verbesserungsmöglichkeiten
Obwohl diese Strategie in der Theorie elegant ist, muss man in der Praxis bedenken:
Auswahl der DatenfrequenzenDas AR-GARCH-Modell unterscheidet sich stark in der Leistung unter verschiedenen Perioden. Die Hochfrequenzdaten liefern mehr Informationen, aber auch mehr Geräusche.
Zeitvariabilität der ParameterIn der aktuellen Umsetzung werden die Parameter AR und GARCH in der Schätzung konstant gehalten, aber die tatsächliche Marktstruktur kann sich ändern.
Auswirkungen auf die TransaktionskostenStatistische Arbitrage-Strategien erfordern in der Regel eine höhere Handelsfrequenz, Gebühren und Schlupfpunkte können nicht ignoriert werden.
Zusammenfassung: Der Wert von statistischen Modellierungen in quantifizierbaren Transaktionen
Die AR-GARCH-Strategie zeigt die starke Kraft der modernen Statistik in der Finanzmodellierung. Es ist nicht nur eine einfache Kombination aus technischen Indikatoren, sondern eine tiefgreifende Untersuchung der statistischen Eigenschaften der Finanzzeitreihen.
Für Quantitative Trader liegt der Wert des Verständnisses solcher Strategien nicht nur in der direkten Anwendung, sondern auch in der Fähigkeit, die Märkte mit statistischer Denkweise zu analysieren. Diese klassischen statistischen Modelle sind heute noch ein wichtiger Grundstein für unser Verständnis der Märkte und die Erstellung von Strategien, da AI und maschinelles Lernen weit verbreitet sind.
/*backtest
start: 2025-04-01 00:00:00
end: 2025-09-09 08:00:00
period: 1h
basePeriod: 1h
exchanges: [{"eid":"Futures_Binance","currency":"BTC_USDT","balance":500000}]
*/
//@version=5
strategy("AR(2)-GARCH Strategy", overlay=true)
//策略参数设置:配置AR模型、GARCH模型和交易信号的各项参数
lengthReg = input.int(50, "AR估计窗口", minval=50, maxval=200);//AR模型回归窗口长度
//GARCH波动率模型参数:控制条件方差的计算
useGarch = input.bool(true, "启用GARCH波动率");//是否启用GARCH波动率建模
garchAlpha = input.float(0.1, "GARCH Alpha", minval=0.01, maxval=0.3, step=0.01);//GARCH模型alpha参数
garchBeta = input.float(0.85, "GARCH Beta", minval=0.5, maxval=0.95, step=0.01);//GARCH模型beta参数
//交易信号生成参数:控制买卖信号的敏感度
stdevFactor = input.float(2.0, "标准差倍数", minval=1.0, maxval=3.0, step=0.1);//交易波段的标准差倍数
//风险控制参数:设置止损止盈水平
stopLossPerc = input.float(2.0, "止损 (%)", minval=0.5, maxval=5.0, step=0.1);//止损百分比
takeProfitPerc = input.float(4.0, "止盈 (%)", minval=1.0, maxval=10.0, step=0.1);//止盈百分比
//RSI过滤器参数:添加技术指标过滤条件
useRsiFilter = input.bool(false, "启用RSI过滤");//是否启用RSI过滤器
rsiLen = input.int(14, "RSI周期", minval=7, maxval=21);//RSI指标计算周期
rsiOB = input.float(70, "RSI超买线", minval=60, maxval=80);//RSI超买阈值
rsiOS = input.float(30, "RSI超卖线", minval=20, maxval=40);//RSI超卖阈值
//数据预处理:计算收益率序列
rawPrice = close;//原始收盘价
returns = math.log(rawPrice / rawPrice[1]);//对数收益率序列
//获取滞后收益率数据:AR(2)模型需要前两期的收益率数据
returns1 = returns[1];//滞后1期的收益率
returns2 = returns[2];//滞后2期的收益率
//计算收益率序列的移动平均值:作为AR模型的均值项
returnsMean = ta.sma(returns, lengthReg);//收益率的简单移动平均
//AR(2)模型系数计算:使用Yule-Walker方程求解自回归系数
//自协方差函数计算:计算不同滞后期的自协方差
calcAutoCovariance(data, lag, length) =>
mean = ta.sma(data, length);//计算数据的均值
sum = 0.0;//协方差累计值
count = 0;//有效数据点计数
for i = lag to length - 1
if not na(data[i]) and not na(data[i-lag])
sum := sum + (data[i] - mean) * (data[i-lag] - mean);//计算协方差分子
count := count + 1;//累计有效数据点
count > 0 ? sum / count : 0.0;//返回协方差值
//计算AR(2)模型所需的自协方差:用于Yule-Walker方程
c0 = calcAutoCovariance(returns, 0, lengthReg);//滞后0期的自协方差(即方差)
c1 = calcAutoCovariance(returns, 1, lengthReg);//滞后1期的自协方差
c2 = calcAutoCovariance(returns, 2, lengthReg);//滞后2期的自协方差
//Yule-Walker方程求解:计算AR(2)模型的两个自回归系数
// φ₁ = (c₁c₀ - c₂c₁) / (c₀² - c₁²)
// φ₂ = (c₂c₀ - c₁²) / (c₀² - c₁²)
denominator = c0 * c0 - c1 * c1;//分母计算
phi1 = denominator != 0 ? (c1 * c0 - c2 * c1) / denominator : 0.0;//第一个自回归系数
phi2 = denominator != 0 ? (c2 * c0 - c1 * c1) / denominator : 0.0;//第二个自回归系数
//AR(2)稳定性检验:确保模型稳定性条件 |φ₁| + |φ₂| < 1 且 |φ₂| < 1
stabilityCheck = math.abs(phi1) + math.abs(phi2);//计算系数绝对值之和
if stabilityCheck >= 0.99 or math.abs(phi2) >= 0.99
scaleFactor = 0.95 / math.max(stabilityCheck, math.abs(phi2) + 0.01);//计算缩放因子
phi1 := phi1 * scaleFactor;//调整第一个系数
phi2 := phi2 * scaleFactor;//调整第二个系数
//AR(2)收益率预测:根据历史收益率和AR系数预测下一期收益率
arReturnPredict = returnsMean + phi1 * (returns1 - returnsMean) + phi2 * (returns2 - returnsMean);//AR(2)预测公式
//计算AR模型的预测残差:用于GARCH建模
arResidual = returns - arReturnPredict;//AR模型的预测残差
//GARCH(1,1)波动率建模:对AR残差进行条件方差建模
var float garchVariance = na;//GARCH方差变量
var float longTermVar = na;//长期方差变量
//长期方差初始化:使用历史残差计算初始方差值
if na(longTermVar) and bar_index > lengthReg
longTermVar := ta.variance(arResidual, lengthReg);//计算长期方差
//GARCH参数调整:确保参数满足收敛条件
adjustedAlpha = garchAlpha;//调整后的alpha参数
adjustedBeta = garchBeta;//调整后的beta参数
sumParam = garchAlpha + garchBeta;//参数和
if sumParam >= 0.999
scale = 0.99 / sumParam;//计算参数缩放比例
adjustedAlpha := garchAlpha * scale;//调整alpha参数
adjustedBeta := garchBeta * scale;//调整beta参数
//GARCH(1,1)递归更新:根据GARCH公式更新条件方差
if useGarch and not na(longTermVar) and not na(arResidual)
if na(garchVariance)
garchVariance := longTermVar;//初始化GARCH方差
else
omega = (1 - adjustedAlpha - adjustedBeta) * longTermVar;//GARCH常数项
garchVariance := omega + adjustedAlpha * math.pow(arResidual[1], 2) + adjustedBeta * garchVariance[1];//GARCH递归公式
//条件标准差计算:从条件方差计算标准差
garchStd = useGarch and not na(garchVariance) ? math.sqrt(math.max(garchVariance, 0.0001)) : ta.stdev(arResidual, 20);//启用GARCH时使用条件标准差,否则使用历史标准差
//收益率空间的置信区间构建:基于AR预测和GARCH波动率
upperReturnBand = arReturnPredict + stdevFactor * garchStd;//上轨:预测收益率加上标准差倍数
lowerReturnBand = arReturnPredict - stdevFactor * garchStd;//下轨:预测收益率减去标准差倍数
//将置信区间转换为价格空间:用于实际交易信号生成
//基于预测收益率计算预测价格
predictedPrice = rawPrice[1] * math.exp(arReturnPredict);//根据预测收益率计算预测价格
upperPriceBand = rawPrice[1] * math.exp(upperReturnBand);//上轨价格
lowerPriceBand = rawPrice[1] * math.exp(lowerReturnBand);//下轨价格
//交易信号生成:基于当前价格相对于置信区间的位置
longSignal = rawPrice < lowerPriceBand;//做多信号:当前价格低于下轨
shortSignal = rawPrice > upperPriceBand;//做空信号:当前价格高于上轨
//RSI过滤器:使用RSI指标过滤交易信号
if useRsiFilter
rsi = ta.rsi(rawPrice, rsiLen);//计算RSI指标
longSignal := longSignal and rsi < rsiOS;//做多信号需要RSI超卖确认
shortSignal := shortSignal and rsi > rsiOB;//做空信号需要RSI超买确认
//策略执行:根据交易信号开仓和平仓
//开仓操作:根据信号建立多头或空头仓位
if longSignal
strategy.entry("Long", strategy.long);//开多仓
if shortSignal
strategy.entry("Short", strategy.short);//开空仓
//风险控制:设置止损止盈条件
if strategy.position_size > 0
strategy.exit("Long Exit", "Long",
stop=strategy.position_avg_price * (1 - stopLossPerc/100),
limit=strategy.position_avg_price * (1 + takeProfitPerc/100));//多仓止损止盈
if strategy.position_size < 0
strategy.exit("Short Exit", "Short",
stop=strategy.position_avg_price * (1 + stopLossPerc/100),
limit=strategy.position_avg_price * (1 - takeProfitPerc/100));//空仓止损止盈
//图表显示:在图表上绘制价格、预测线和交易信号
//主要价格线和预测线:显示实际价格和基于收益率预测的价格
plot(rawPrice, color=color.white, linewidth=1, title="价格");//绘制实际价格线
plot(predictedPrice, color=color.blue, linewidth=2, title="预测价格");//绘制预测价格线
plot(upperPriceBand, color=color.red, linewidth=1, title="上轨");//绘制上轨线
plot(lowerPriceBand, color=color.green, linewidth=1, title="下轨");//绘制下轨线
//交易信号标记:在图表上标记买卖信号点
plotshape(longSignal, style=shape.triangleup, location=location.belowbar,
color=color.green, size=size.small, title="买入");//标记买入信号
plotshape(shortSignal, style=shape.triangledown, location=location.abovebar,
color=color.red, size=size.small, title="卖出");//标记卖出信号