Hablemos de cómo optimizar los parámetros de varios modelos de trading programático

• #### El Alto Parámetro y las Islas Parámetros

　 Un principio importante en la optimización de parámetros es buscar alturas de parámetros en lugar de islas de parámetros. Las llamadas alturas de parámetros, que significan que existe un rango de parámetros más amplio, en el que el modelo obtiene mejores resultados, generalmente forman una distribución casi normal con el centro de la alturas. Las llamadas islas de parámetros, que significan que el modelo solo tiene un buen rendimiento cuando los valores de los parámetros se encuentran en un rango muy pequeño, y cuando los parámetros se desvían de ese valor, el rendimiento del modelo varía significativamente.

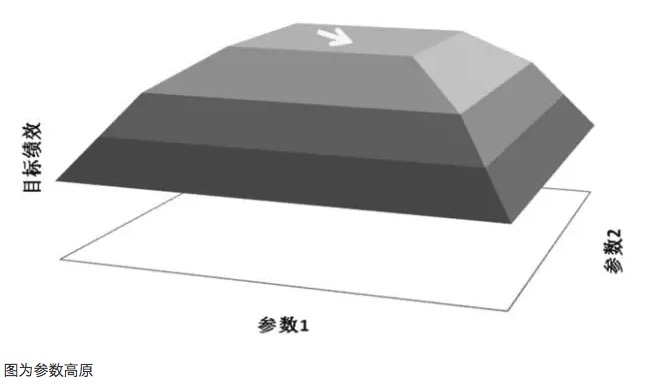
• #### El gráfico es el Parameter Plateau.

Tomando como ejemplo el diagrama de la platea de parámetros y el diagrama de la isla de parámetros, supongamos que un modelo de negociación tiene dos parámetros, respectivamente el parámetro 1 y el parámetro 2, cuando se realiza una prueba de recorrido de los dos parámetros, se obtiene un gráfico de rendimiento tridimensional. Una buena distribución de parámetros debe ser el diagrama de la platea de parámetros, incluso cuando la configuración de los parámetros se desvía, el rendimiento de ganancias del modelo aún puede ser garantizado.

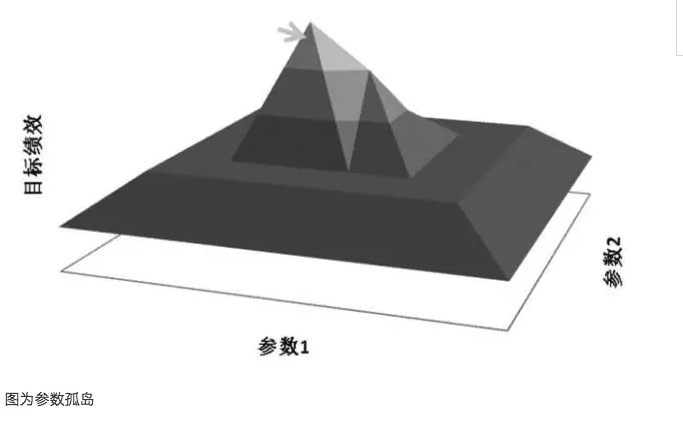
En general, si el rendimiento de un sistema de parámetros cercanos es muy diferente del rendimiento de un parámetro óptimo, entonces este parámetro óptimo puede ser el resultado de una suma de más, y puede considerarse matemáticamente como una solución de singularidad, en lugar de la solución de valor máximo que se busca. Desde el punto de vista matemático, la singularidad es inestable, y en situaciones de incertidumbre futura, el parámetro óptimo puede convertirse en un parámetro mínimo una vez que cambien las características del mercado.

El exceso de ajuste está relacionado con la muestra seleccionada. Si la muestra seleccionada no representa la característica general del mercado y solo ajusta los parámetros para que los resultados de la prueba alcancen el valor esperado positivo, esta práctica es indudablemente autoengañosa, y el valor de los parámetros obtenidos es el parámetro ineficaz del exceso de ajuste. Por ejemplo, al analizar el exceso de ajuste de los parámetros, el modelo de negociación presenta un aumento súbito de la rentabilidad en los valores 35 y 63, respectivamente, y si los indicadores correspondientes del modelo seleccionan los parámetros 35 y 63, el rendimiento del modelo parece ser perfecto, pero en realidad es un típico efecto de islas de parámetros.

La principal contradicción entre el exceso de ajuste y la optimización de parámetros es que los parámetros óptimos obtenidos con la optimización de parámetros de un modelo se basan solo en una muestra de datos históricos que ya han ocurrido, mientras que el comportamiento futuro es dinámico y tiene similitudes y variaciones con respecto al comportamiento histórico. Los diseñadores de modelos pueden encontrar los parámetros de modelos que mejor han funcionado en la historia, pero este parámetro no es necesariamente el mejor en las aplicaciones reales del modelo futuro, y más aún, los parámetros de modelos que mejor han funcionado en la historia pueden ser parámetros que funcionan mal en las batallas de modelos futuros, incluso con grandes pérdidas.

Además, la altiplanicie de parámetros y el aislamiento de parámetros a menudo también están relacionados con el número de transacciones. Si el número de transacciones del modelo es menor, a menudo se puede encontrar un punto de parámetros adecuado, lo que hace que el modelo gane en todas las transacciones, el modelo de ganancias después de la optimización de estos parámetros refleja una mayor casualidad. Si el número de transacciones del modelo es mayor, la casualidad de la ganancia del modelo disminuye, y refleja más la inevitabilidad y regularidad de la ganancia.

• #### Métodos para optimizar los parámetros

Una vez que se conoce el plano de los parámetros y el islote de los parámetros, la optimización de los parámetros es muy importante, especialmente cuando hay varios parámetros en el modelo (llamados arrays de parámetros), a menudo el valor de un parámetro afecta a la distribución de otro plano de los parámetros. Entonces, ¿cómo se optimiza el array de parámetros?

Un método de convergencia gradual consiste en que primero se optimiza un parámetro por separado, se fija después de obtener su valor óptimo, y luego se optimiza otro parámetro, se fija después de obtener su valor óptimo. Así se recorre hasta que el resultado de la optimización no cambie. Por ejemplo, un modelo de comercio de compra y venta cruzado lineal, con dos parámetros independientes, el ciclo corto de la línea media N1 y el ciclo largo N2. Primero se fija N2 como 1, se hace una selección de prueba en N1 en un rango de valores de 1 a 100 para encontrar el valor óptimo y finalmente se obtiene el parámetro óptimo 8 y se fija; luego se optimiza N2 entre 1 y 200 y se obtiene el valor óptimo 26 y se fija; nuevamente se realiza una segunda ronda de optimización de N1 y se obtiene el nuevo parámetro óptimo 10 y se fija; finalmente, se optimiza N2 y se fija el valor óptimo 28 y así se recorre hasta que el resultado de la optimización no cambie.

Otro método es utilizar una plataforma de diseño de software programado con funciones de cálculo más potentes, calcular directamente la distribución entre la función objetivo y el conjunto de parámetros, y luego buscar la distribución de la diferencia multidimensional, definir un umbral de diferencia, cuyo valor absoluto de diferencia sea menor que el correspondiente tamaño multidimensional más grande, el más alto radio de recorte dentro de la dimensión multidimensional, seleccionado como el valor de parámetro más estable.

Además de los métodos de optimización de parámetros, la selección de muestras de datos también es un factor importante. Los modelos que usan el seguimiento de la tendencia como idea de negociación funcionan mejor en situaciones de tendencia, y las estrategias que usan el precio alto y bajo como idea de negociación funcionan mejor en situaciones de oscilación. Por lo tanto, en la optimización de parámetros, se necesita eliminar adecuadamente las acciones que coinciden con las ideas de negociación para considerar las ganancias y aumentar los datos de las acciones que no coinciden con las ideas de la estrategia para considerar las pérdidas.

Por ejemplo, los futuros de los índices de acciones, desde el inicio de la cotización en 2010 y desde el segundo semestre de 2014, cuando se produjo el bull market extremo, han sido unilaterales. Sin duda, todos los modelos de tendencia obtienen buenos resultados. Sin embargo, si también incluimos estos datos de tendencia extrema en la muestra para optimizar los parámetros, los parámetros del modelo obtenidos no necesariamente son los mejores.

Por ejemplo, supongamos que un modelo tiene dos parámetros, los resultados de la prueba del parámetro A son muy buenos en un solo período de tiempo y se comportan generalmente en otros períodos; los resultados de la prueba del otro parámetro B son menos buenos en un solo período de tiempo y se comportan mejor en otros períodos, y la distribución entre los períodos es más uniforme que el parámetro A. Incluso si el parámetro A es más alto que el parámetro B en un conjunto de indicadores de riesgo-beneficio probados en toda la muestra de datos, preferimos elegir el parámetro B, ya que el parámetro B es relativamente más estable y no depende de una muestra en particular.

En resumen, en la construcción de modelos de transacciones programadas, por un lado, se puede mejorar el modelo mediante la optimización de los parámetros, para que el modelo se adapte mejor a los patrones de fluctuación de los precios y mejore el rendimiento de la inversión; por otro lado, se debe evitar la adaptación excesiva a la optimización de los parámetros, lo que reduce considerablemente la adaptabilidad del modelo a los cambios en las condiciones de mercado.

La mayoría de los comerciantes programados no tienen acceso a la información.