Regresión lineal - método de mínimos cuadrados

• ### Una introducción

Durante este tiempo de aprendizaje de la máquina de cálculo, aprendió el cálculo de la regresión logística en el capítulo 5, y se sintió bastante cansado. Se remonta a la fuente, desde el cálculo de la regresión logística hasta el cálculo de la regresión lineal, y luego al cálculo de la decimal mínima. Finalmente, se calificó para el cálculo de la decimal mínima de la decimal mínima de la decimal mínima de la decimal mínima de la decimal mínima. El cubo de minimizar la binomial es una implementación de la fórmula de experiencia en el problema de optimización. Conocer su principio es útil para entender el cubo de regreso logístico y el cubo de aprendizaje de la máquina vectorial de soporte de cubo.

• ### 2 - Conocimiento de antecedentes

El contexto histórico de la aparición de la fracción de la menor ecuación es muy interesante.

En 1801, el astrónomo italiano Giuseppe Piazzi descubrió el primer asteroide de la estrella de Valle. Después de 40 días de observaciones de seguimiento, Piazzi perdió la posición de la estrella de Valle debido a que la estrella de Valle se encontraba detrás del Sol. Posteriormente, los científicos de todo el mundo utilizaron los datos de observación de Piazzi para comenzar a buscar la estrella de Valle, pero no hubo resultados según los resultados calculados por la mayoría de las personas.

El método de Gauss para la multiplicación de los dos mínimos fue publicado en 1809 en su libro La teoría del movimiento de los cuerpos celestes, mientras que el científico francés Léger descubrió el principio de la multiplicación de los dos mínimos de Gauss de forma independiente en 1806, pero no fue conocido en ese momento. Los dos se discutieron sobre quién fue el primero en crear el principio de multiplicación de los dos mínimos.

En 1829, Gauss proporcionó una demostración de que la optimización de la multiplicación por el segundo mínimo era más eficaz que otros métodos, véase el Teorema de Gauss-Markov.

• ### El uso del conocimiento

El núcleo de la fórmula de la minúscula bimetálica es garantizar el cuadrado y la minúscula de todas las desviaciones de datos.

Supongamos que estamos recopilando datos de la longitud y la anchura de algunas naves de guerra.

A partir de estos datos, dibujamos un mapa de dispersión en Python:

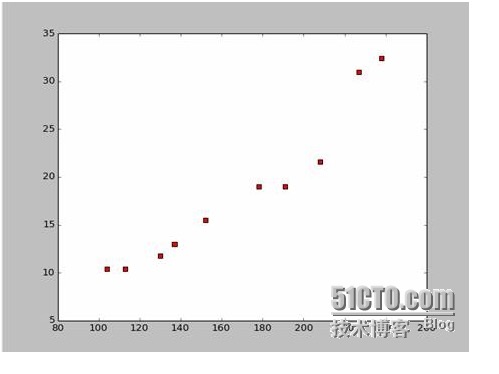
El código para dibujar un mapa de puntos es el siguiente:

  import numpy as np                # -*- coding: utf-8 -*
  import os
  import matplotlib.pyplot as plt
  def drawScatterDiagram(fileName): # 改变工作路径到数据文件存放的地方
      os.chdir("d:/workspace_ml")
      xcord=[];ycord=[]
      fr=open(fileName)
      for line in fr.readlines():
          lineArr=line.strip().split()
          xcord.append(float(lineArr[1]));ycord.append(float(lineArr[2]))
      plt.scatter(xcord,ycord,s=30,c='red',marker='s')
      plt.show()

Si tomamos los dos primeros puntos, 238, 32, 4 y 152, 15, 5 obtendremos las dos ecuaciones. 152*a+b=15.5 328*a+b=32.4 Y si lo hacemos de esta manera, entonces a es igual a 0.197 y b es igual a -14.48. En ese caso, obtendremos un gráfico de encaje como este:

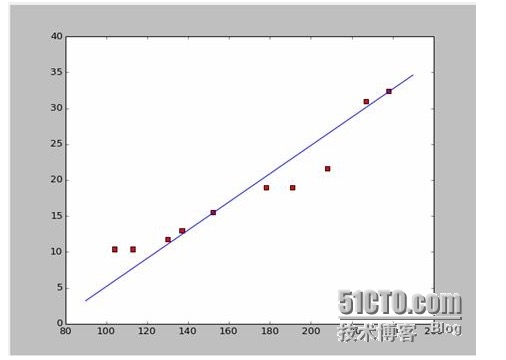
Bien, ahora viene la nueva pregunta, ¿es a y b la solución óptima? En términos profesionales, ¿es a y b el parámetro óptimo del modelo?

La respuesta es: el cuadrado y el mínimo de la garantía de la desviación de todos los datos. En cuanto a los principios, veremos más adelante cómo usar esta herramienta para calcular el mejor a y b.

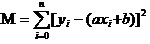
Lo que vamos a hacer ahora es encontrar el mínimo de M para a y b.

En realidad, la ecuación es una función binaria con a, b como su propia variable y M como su variable de la razón.

Recuerde cómo la función unitaria en los números altos tiene un valor extremo. Utilizamos la derivada como herramienta. En las funciones binarias, seguimos usando derivadas. Por lo tanto, si buscamos la derivada parcial de M, obtendremos un conjunto de ecuaciones.

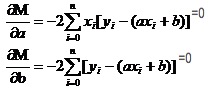
En ambas ecuaciones, se conocen los valores de xi y de y.

Es muy fácil encontrar a y b. Como los datos son de Wikipedia, voy a usar las respuestas para dibujar una imagen que encaje:

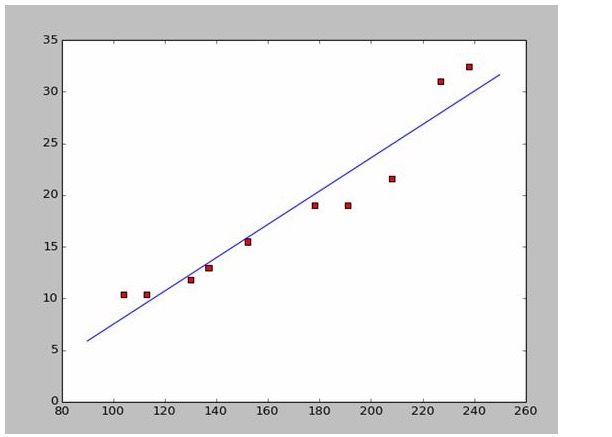
  # -*- coding: utf-8 -*importnumpy as npimportosimportmatplotlib.pyplot as pltdefdrawScatterDiagram(fileName):
  # 改变工作路径到数据文件存放的地方os.chdir("d:/workspace_ml")xcord=[];
  # ycord=[]fr=open(fileName)forline infr.readlines():lineArr=line.strip().split()xcord.append(float(lineArr[1]));
  # ycord.append(float(lineArr[2]))plt.scatter(xcord,ycord,s=30,c='red',marker='s')
  # a=0.1965;b=-14.486a=0.1612;b=-8.6394x=np.arange(90.0,250.0,0.1)y=a*x+bplt.plot(x,y)plt.show()
  # -*- coding: utf-8 -*
  import numpy as np
  import os
  import matplotlib.pyplot as plt
  def drawScatterDiagram(fileName):
      #改变工作路径到数据文件存放的地方
      os.chdir("d:/workspace_ml")
      xcord=[];ycord=[]
      fr=open(fileName)
      for line in fr.readlines():
          lineArr=line.strip().split()
          xcord.append(float(lineArr[1]));ycord.append(float(lineArr[2]))
      plt.scatter(xcord,ycord,s=30,c='red',marker='s')
      #a=0.1965;b=-14.486
      a=0.1612;b=-8.6394
      x=np.arange(90.0,250.0,0.1)
      y=a*x+b
      plt.plot(x,y)
      plt.show()

• ### Cuatro principios para investigar

En la adecuación de datos, ¿por qué se optimizan los parámetros del modelo con el cuadrado de la diferencia entre los datos de predicción del modelo y los datos reales en lugar de los valores absolutos y mínimos?

Esta pregunta ya ha sido respondida, ver enlaces (http://blog.sciencenet.cn/blog-430956-621997).

Personalmente encuentro esta explicación muy interesante. Especialmente la hipótesis que contiene: todos los puntos que se desvían de f (x) son ruidosos.

La mayor distancia de un punto indica que el ruido es mayor, y la menor probabilidad de que este punto aparezca. Entonces, ¿cuál es la relación entre el grado de desviación x y la probabilidad de aparición f (x)?

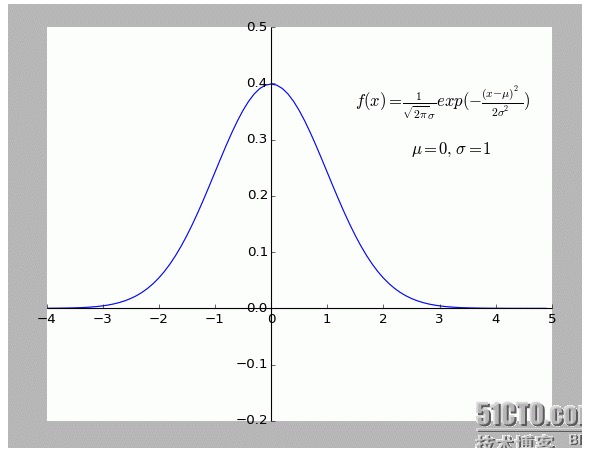
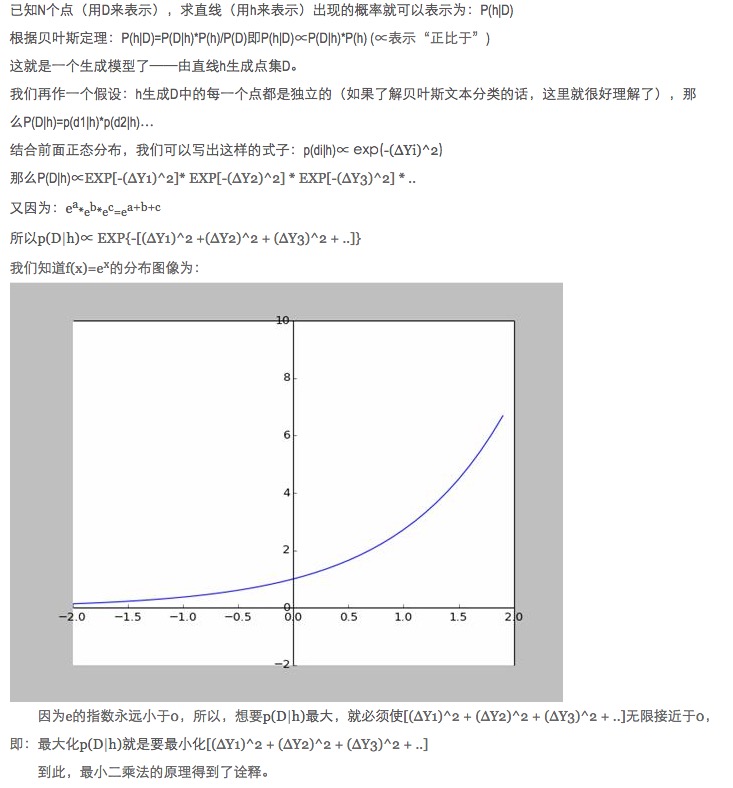
• ### Cinco, ampliar y extender.

Las situaciones mencionadas son bidimensionales, es decir, solo hay una autovariable. Pero en el mundo real, la superposición de múltiples factores que afectan el resultado final, es decir, la autovariable puede tener varias situaciones.

Para las funciones metalinéricas generales N, la matriz inversa en la columna de algebra lineal es la solución correcta; como no se ha encontrado un ejemplo adecuado, se deja aquí como un argumento.

Por supuesto, la naturaleza es más una adecuación de polinomios que una simple linealidad, que es un contenido más avanzado.

• Referencias

  • Sección de Matemáticas Superior (Sexta Edición)
  • Aritmética de la algebra lineal (Publicado por la Universidad de Pekín)
  • Enciclopedia interactiva:El segundo mínimo.
  • Wikipedia: La multiplicación por el segundo mínimo
  • Ciencia y tecnología:¿Cuál es el número mínimo de la ecuación?

Las obras originales, las reproducciones permitidas, las reproducciones deben indicar la fuente original del artículo en forma de hipervínculo, la información del autor y esta declaración. De lo contrario, se responsabilizará legalmente. http://sbp810050504.blog.51cto.com/2799422/1269572