Interesante comprensión del método Bayes ingenuo

NavieBayes

  Hay muchas situaciones en la vida que requieren clasificar, como la clasificación de noticias, la clasificación de pacientes, etc. Para que todos puedan entender la imagen, este artículo presenta un algoritmo de clasificación simple y comúnmente utilizado desde la aplicación práctica: el simple Bayes (Navie Bayes classifier).

• 01 Ejemplos de clasificación de pacientes

Comenzaré con un ejemplo, y verás que el clasificador de Bayes es muy fácil de entender. Un hospital recibió a seis pacientes en una consulta en la mañana, como se muestra en la siguiente tabla.

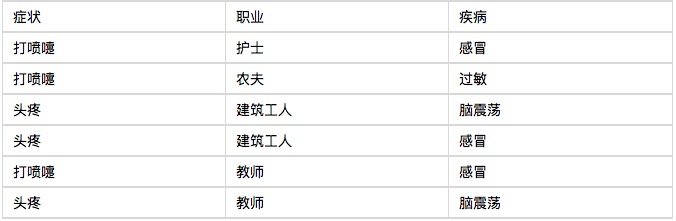
Ahora viene el séptimo paciente, un trabajador de la construcción que estornuda. ¿Cuál es la probabilidad de que tenga un resfriado?

  P(A|B) = P(B|A) P(A) / P(B)

¿Qué es lo que está pasando?

  P(感冒|打喷嚏x建筑工人) 
  　　　　= P(打喷嚏x建筑工人|感冒) x P(感冒) 
  　　　　/ P(打喷嚏x建筑工人)

Supongamos que las dos características de “espirrar” y “trabajadores de la construcción” son independientes, por lo tanto, la ecuación anterior se convierte en

  P(感冒|打喷嚏x建筑工人) 
  　　　　= P(打喷嚏|感冒) x P(建筑工人|感冒) x P(感冒)
  　　　　/ P(打喷嚏) x P(建筑工人)

Esto es calculable.

  P(感冒|打喷嚏x建筑工人) 
  　　　　= 0.66 x 0.33 x 0.5 / 0.5 x 0.33 
  　　　　= 0.66

Por lo tanto, el trabajador de la construcción que estornuda tiene una probabilidad del 66% de haber contraído un resfriado. También se puede calcular la probabilidad de que el paciente sufra de una alergia o de una conmoción cerebral. Al comparar estas probabilidades, se puede saber cuál es la enfermedad más probable que tenga.

Este es el método básico del clasificador de Bayes: basado en datos estadísticos, se calcula la probabilidad de cada categoría en función de ciertas características, de modo que se logra la clasificación.

• 02 Fórmulas para el clasificador básico simple

Supongamos que un individuo tiene n características, respectivamente F1, F2, … y Fn. Existen m categorías, respectivamente C1, C2, … y Cm. El clasificador de Bayes es la clasificación que calcula la mayor probabilidad, es decir, el valor máximo de la siguiente fórmula:

  P(C|F1F2...Fn) 
  　　   = P(F1F2...Fn|C)P(C) / P(F1F2...Fn)

Dado que P ((F1F2…Fn) es igual para todas las categorías, se puede omitir y la pregunta se convierte en

  P(F1F2...Fn|C)P(C)

El valor máximo de

El clasificador simplista de Bayes va más allá, asumiendo que todos los atributos son independientes entre sí, y por lo tanto

  P(F1F2...Fn|C)P(C) 
  　　   = P(F1|C)P(F2|C) ... P(Fn|C)P(C)

Cada uno de los elementos de la derecha de la ecuación se puede obtener de la estadística, de esta manera se puede calcular la probabilidad de que cada categoría corresponda, para encontrar la clase con la mayor probabilidad.

Aunque la hipótesis de que “todas las características son independientes entre sí” es poco probable en la realidad, puede simplificar considerablemente los cálculos, y hay estudios que muestran que tiene poco impacto en la precisión de los resultados de la clasificación.

A continuación se muestran dos ejemplos de cómo se puede utilizar el clasificador báyese sencillo:

• 03 Clasificación de las cuentas

De acuerdo con una muestra de estadísticas de un sitio web de la comunidad, 89% de las 10.000 cuentas son cuentas reales (con C0) y 11% son cuentas falsas (con C1). A continuación, las estadísticas se usan para juzgar la autenticidad de una cuenta.

  C0 = 0.89 C1 = 0.11

Supongamos que una cuenta tiene las siguientes tres características: F1: Número de registros/días de registro F2: Número de amigos/días de registro F3: Si se utiliza una imagen real (la imagen real es 1, la imagen no real es 0) F1 = 0.1  F2 = 0.2  F3 = 0

¿Es una cuenta real o falsa? El método es usar un clasificador básico simple para calcular el valor de la siguiente fórmula:

P(F1|C)P(F2|C)P(F3|C)P©

Aunque estos valores se pueden obtener a partir de estadísticas, hay un problema: F1 y F2 son variables continuas, y no es conveniente calcular la probabilidad de un valor en particular. Una técnica es convertir los valores continuos en valores dispersos y calcular la probabilidad de un intervalo.[0, 0.05]、(0.05, 0.2)、[0.2, +∞] tres intervalos, y luego calcular la probabilidad de cada uno de ellos. En nuestro ejemplo, F1 es igual a 0.1, que cae en el segundo intervalo, por lo que se utiliza la probabilidad de ocurrencia del segundo intervalo para calcular.

Según las estadísticas:

P(F1|C0) = 0.5, P(F1|C1) = 0.1  P(F2|C0) = 0.7, P(F2|C1) = 0.2  P(F3|C0) = 0.2, P(F3|C1) = 0.9

Por lo tanto

P(F1|C0) P(F2|C0) P(F3|C0) P(C0)  = 0.5 x 0.7 x 0.2 x 0.89  = 0.0623 P(F1|C1) P(F2|C1) P(F3|C1) P(C1)  = 0.1 x 0.2 x 0.9 x 0.11  = 0.00198 Se puede ver que, aunque este usuario no usa una imagen de identidad real, tiene más de 30 veces más probabilidades de ser una cuenta real que una falsa, por lo que la cuenta se considera real.

• 04 Clasificación por género

Las siguientes son estadísticas de un grupo de características del cuerpo humano.

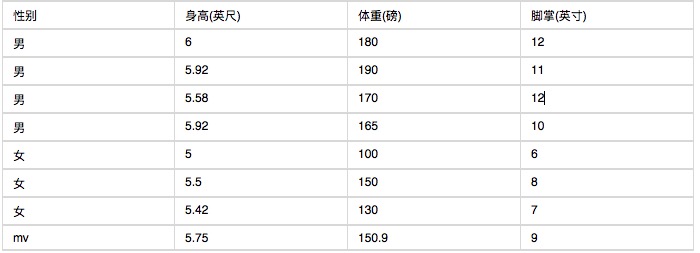
Si se sabe que una persona es de 6 pies de altura, 130 libras de peso y 8 pulgadas de altura en las palmas de sus pies, ¿por favor pregunte si es hombre o mujer? Calcule el valor de la siguiente fórmula según el clasificador báyeso simple.

P (talla y sexo) x P (peso y sexo) x P (patas y sexo) x P (género)

La dificultad aquí es que, dado que la altura, el peso y las palmas de las manos son variables continuas, no se puede usar el método de las variables discontinuas para calcular la probabilidad. Y debido a que la muestra es muy pequeña, no se puede dividir en intervalos. ¿Qué hacer?

Con estos datos se puede calcular la clasificación por sexo.

P (talla = 6 años de edad) x P (peso = 130 años de edad) x P (palmas = 8 años de edad) x P (hombre)

= 6.1984 x e-9

P (talla = 6 mujeres) x P (peso = 130 mujeres) x P (palmas = 8 mujeres) x P (mujer)

= 5.3778 x e-4

Como se puede ver, la probabilidad de que sea una mujer es casi 10.000 veces mayor que la de que sea un hombre, por lo que la persona es considerada una mujer.

El número público de WeChat de la cumbre de Yan’an