Comprensión intuitiva de la cointegración

Introducción: El objetivo de este artículo es introducir el concepto de integración de manera intuitiva, para ayudar a entender su significado básico, los motivos que propone el concepto, y los sencillos escenarios de aplicación.

• Descripción del proyecto

Aquí solo quiero señalar que la definición intuitiva de integración no implica una definición estricta de símbolos matemáticos y una rigurosa inferencia de fórmulas.

Si estáis interesados, podéis ver: Wikipedia Cointegration. La clase de cuantificación también explorará su contenido en profundidad en el futuro.

¿Por qué la igualdad/coherencia?

Cuando se habla de integración, hay que hablar de estabilidad.

En pocas palabras, estabilidad es la propiedad de una secuencia que permanece estable y no cambia con el tiempo, y es una de las propiedades que más nos gustan al hacer predicciones analíticas de los datos. Si un conjunto de datos de la secuencia de tiempo es estable, significa que sus medias y diferencias permanecen invariables, de modo que podemos usar algunas técnicas estadísticas en la secuencia de forma conveniente.

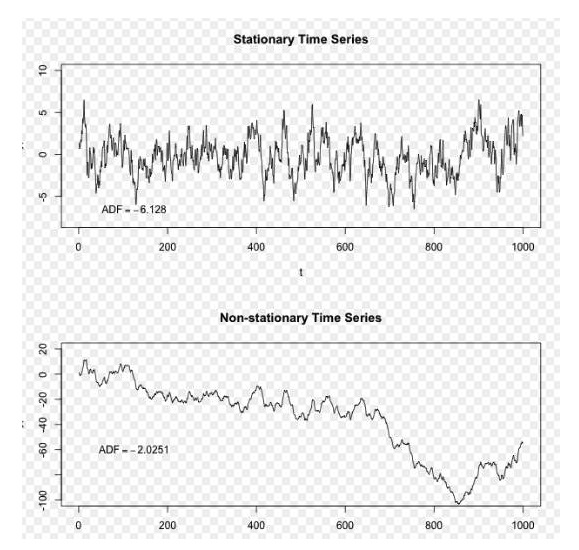
La imagen fue tomada de Wikipedia.

En el gráfico de arriba, la secuencia de arriba es una secuencia estable, y podemos ver que fluctúa constantemente alrededor de una media a largo plazo, y la de abajo es una secuencia no estable, y podemos ver que su media a largo plazo es variable.

Para dar un ejemplo de aplicación, si la secuencia de precios de un activo (o la diferencia de precios entre dos secuencias) es estable, entonces cuando se desvía de su valor promedio, se puede esperar que el precio regrese a este valor promedio en algún momento futuro. Podemos usar esta propiedad para invertir y obtener ganancias. Supongamos que la media a largo plazo de una acción es de 9 dólares y su valor actual es de 8 dólares.

Este es un gráfico de precios de acciones de naturaleza estabilizadora:

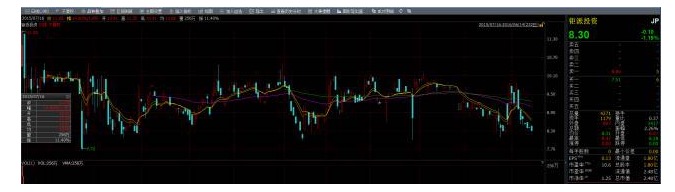
La estabilidad es muy útil, pero en la realidad, la gran mayoría de las acciones son no estables, entonces ¿podemos aprovechar la estabilidad para obtener ganancias? La respuesta es sí, entonces la cointegración está en juego! Si dos conjuntos de secuencias no son estables, pero su combinación lineal puede obtener una secuencia estable, entonces decimos que estos dos conjuntos de datos de secuencias de tiempo tienen la propiedad de la cointegración, y también podemos usar la propiedad estadística en la secuencia de esta combinación. Pero es necesario señalar que la cointegración no es una relación de correlación.

Por ejemplo, si la diferencia entre los dos conjuntos de datos de la secuencia temporal es constante, podemos invertir en beneficio de la estabilidad de la diferencia: cuando el precio de las dos acciones es demasiado diferente, según la estabilidad esperamos que la diferencia de precios se acerque, por lo que compramos acciones de bajo precio, vendemos acciones de alto precio y esperamos que el precio regrese para obtener ganancias.

Así es como surgió el comercio de pares.

• Estabilidad y métodos de ensayo

Estrictamente hablando, la estabilidad se puede dividir en estabilidad estricta (estrictamente estacionaria) y estabilidad débil (o estabilidad por covarianza, estacionaria, etc.). La estabilidad estricta es cuando una secuencia siempre tiene una función de distribución invariable, mientras que la estabilidad débil es cuando la secuencia tiene una cantidad de constantes descriptivas que no cambian. Todas las secuencias estables y fuertes satisfacen la característica de estabilidad débil, pero no lo contrario. Lo que generalmente llamamos estabilidad es estabilidad débil.

Ejemplo de una aplicación

En primer lugar hay que señalar que la correlación de coherencia no es una correlación de correlación. Construimos artificialmente los dos conjuntos de datos para ver la correlación de coherencia de forma intuitiva. import numpy as np import pandas as pd import seaborn import statsmodels import matplotlib.pyplot as plt from statsmodels.tsa.stattools import coint

Datos de construcción

En primer lugar, construimos dos grupos de datos, cada uno de 100 de longitud. El primer grupo de datos es de 100 más un elemento de tendencia descendente más una distribución normal estándar. El segundo grupo de datos se basa en el primer grupo de datos más 30, más una distribución normal estándar adicional.

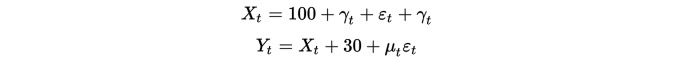
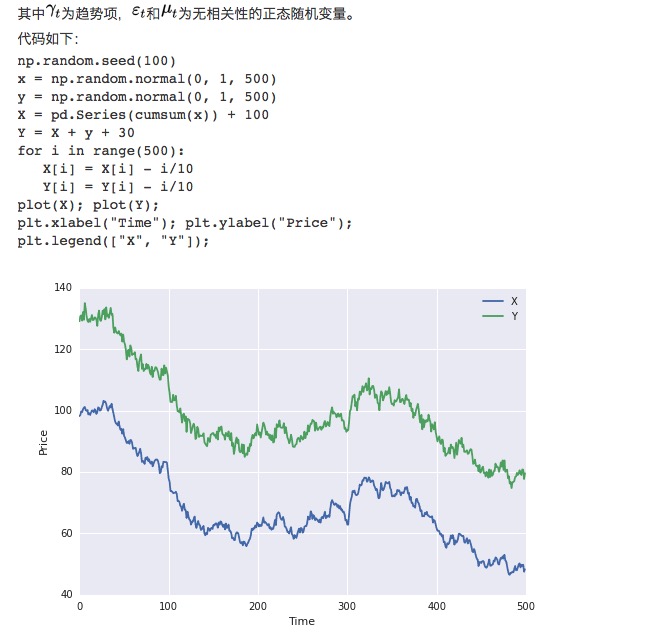
Obviamente, ambos grupos de datos son no estables, ya que los promedios cambian con el tiempo. Pero ambos grupos de datos son coherentes, ya que sus secuencias diferenciales son estables:

plot(Y-X); plt.axhline((Y-X).mean(),color=“red”, linestyle=“–”); plt.xlabel(“Time”); plt.ylabel(“Price”); plt.legend([“Y-X”, “Mean”]);

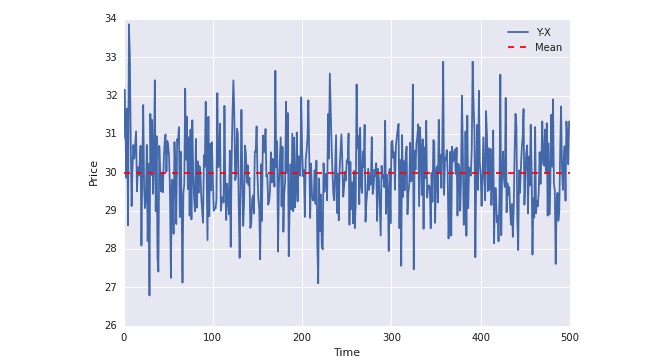
En el gráfico de arriba, se puede ver que la línea azul ha estado fluctuando alrededor del promedio. El promedio no cambia con el tiempo (en realidad, la diferencia no cambia con el tiempo).

• Conclusión

Si la integración se explica desde el punto de vista matemático, será más compleja, y las clases de cuantificación posteriores estarán involucradas. Solo hicimos una simple introducción a nivel de comprensión (nivel-0) con el objetivo de que la integración se combine mejor con aplicaciones reales.

Por favor, comparta y transfiera su experiencia de clases cuantitativas a la dirección de Love Ask.