Aplicación Naive Bayes de Python

En palabras más simples, un clasificador naive de Bayes asume que una característica de la clasificación no está relacionada con las otras características de la misma. Por ejemplo, si una fruta es redonda y redonda y tiene un diámetro de aproximadamente 3 pulgadas, entonces la fruta puede ser una manzana. Incluso si estas características dependen entre sí o dependen de otras características, el clasificador naive de Bayes asume que estas características sugieren que la fruta es una manzana independientemente.

• #### Los modelos básicos sencillos son fáciles de construir y son muy útiles para grandes conjuntos de datos. Aunque son simples, los modelos básicos sencillos superan los métodos de clasificación muy complejos.

El teorema de Bayes proporciona un método para calcular la probabilidad de retrospectiva P (c y dx) a partir de P ©, P (x) y P (x y dx). Consulte la siguiente ecuación:

¿Qué es lo que está sucediendo?

P © {\displaystyle \sigma © } es la probabilidad de retrospectiva de la clase (objetivo) con una variable de predicción (propiedad) conocida P © es la prioridad de la clase P (x) {\displaystyle \sigma (x) } es la probabilidad, es decir, la probabilidad de predicir una variable con una clase conocida. P (x) es la probabilidad previa de la variable de predicción Ejemplo: Vamos a entender el concepto con un ejemplo. A continuación, tengo un conjunto de entrenamiento para el clima y la correspondiente variable objetivo de juego. Ahora, necesitamos clasificar a los participantes que juegan y a los que no juegan en función de las condiciones climáticas.

Paso 1: Convierta el conjunto de datos en una tabla de frecuencias.

Paso 2: Crea una tabla de probabilidad utilizando el cuadro similar cuando la probabilidad de Overcast es de 0.29 y la probabilidad de jugar es de 0.64.

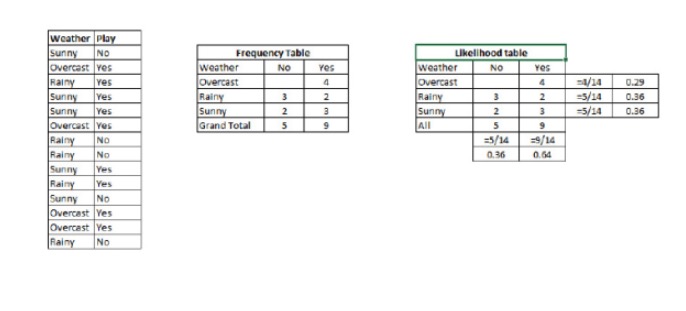
Paso 3: Ahora, utilicemos la ecuación básica de Bayes para calcular la probabilidad de retroceso de cada clase. La clase con mayor probabilidad de retroceso es el resultado previsto.

Pregunta: ¿Es correcto que los participantes puedan jugar si el tiempo es bueno?

Podemos usar el método que hemos discutido para resolver este problema. Entonces P (juego) = P (juego) / P (juego).

Así que tenemos P = ³⁄₉ = 0.33, P = ⁵⁄₁₄ = 0.36, P = ⁹⁄₁₄ = 0.64.

Ahora, P (juego) = 0.33 * 0.64 / 0.36 = 0.60, tiene una mayor probabilidad.

Prudent Bayes utiliza un método similar para predecir la probabilidad de diferentes categorías a través de diferentes atributos. Este algoritmo se usa comúnmente para clasificar texto, así como para problemas que involucran varias categorías.

• #### El código de Python:

  #Import Library
  from sklearn.naive_bayes import GaussianNB
  　　
  #Assumed you have, X (predictor) and Y (target) for training data set and x_test(predictor) of test_dataset

Create SVM classification object model = GaussianNB()

there is other distribution for multinomial classes like Bernoulli Naive Bayes, Refer link

Train the model using the training sets and check score

model.fit(X, y) #Predict Output predicted= model.predict(x_test)