Reflexiones sobre estrategias de trading de alta frecuencia (2)
 1
1
 3416
3416
El artículo analiza principalmente estrategias de trading de alta frecuencia, centrándose en el modelado del volumen acumulado y los shocks de precios. En este artículo se propone un modelo preliminar de colocación óptima de órdenes analizando el impacto de las transacciones individuales, los shocks de precios de intervalo fijo y el volumen de transacciones sobre los precios. Este modelo intenta encontrar la posición comercial óptima basándose en la comprensión de los shocks de volumen y precio. Se discuten en profundidad los supuestos del modelo y se realiza una evaluación preliminar de la colocación óptima de pedidos comparando los retornos esperados reales y los previstos por el modelo.
Modelado de volumen acumulado
El artículo anterior derivó la expresión de probabilidad de que un volumen de transacción única sea mayor que un valor determinado:
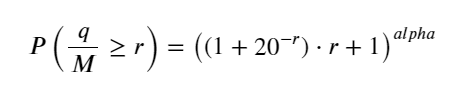
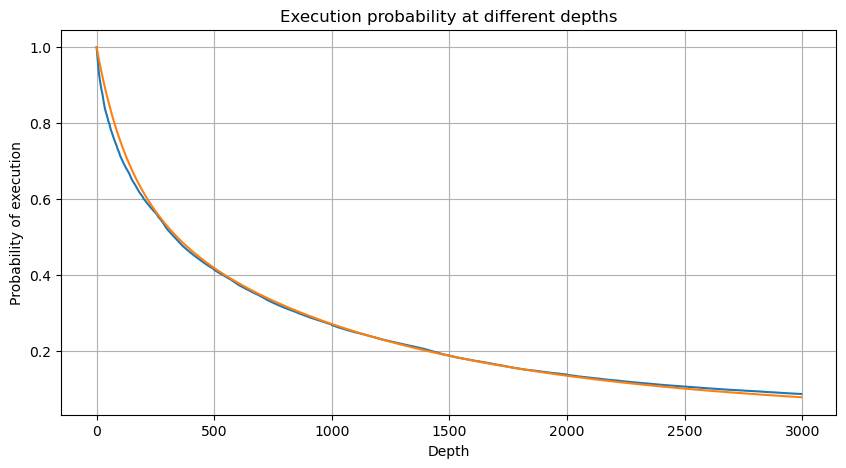
También nos preocupa la distribución del volumen de negociación durante un período de tiempo, que intuitivamente debería estar relacionado con el volumen de cada transacción y la frecuencia de las órdenes. A continuación, los datos se procesan a intervalos fijos. Grafique su distribución como se indica arriba.
from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
trades = pd.read_csv('HOOKUSDT-aggTrades-2023-01-27.csv')
trades['date'] = pd.to_datetime(trades['transact_time'], unit='ms')
trades.index = trades['date']
buy_trades = trades[trades['is_buyer_maker']==False].copy()
buy_trades = buy_trades.groupby('transact_time').agg({
'agg_trade_id': 'last',
'price': 'last',
'quantity': 'sum',
'first_trade_id': 'first',
'last_trade_id': 'last',
'is_buyer_maker': 'last',
'date': 'last',
'transact_time':'last'
})
buy_trades['interval']=buy_trades['transact_time'] - buy_trades['transact_time'].shift()
buy_trades.index = buy_trades['date']
Combina el volumen de transacciones cada 1 s, elimina la parte en la que no se produjo ninguna transacción y utiliza la distribución de transacciones individuales anterior para ajustar. Se puede ver que el resultado es mejor. Si todas las transacciones dentro de 1 s se consideran transacciones individuales, este problema se convierte en Se ha convertido en un problema resuelto. Sin embargo, cuando el ciclo se alarga (en relación con la frecuencia de la transacción), se descubre que el error aumenta, y las investigaciones han descubierto que este error es causado por el término de corrección de la distribución de Pareto anterior. Esto significa que, a medida que el ciclo se alarga e incluye más transacciones individuales, la combinación de múltiples transacciones se aproxima a la distribución de Pareto. En este caso, se debe eliminar el término de corrección.
df_resampled = buy_trades['quantity'].resample('1S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]
buy_trades
| agg_trade_id | price | quantity | first_trade_id | last_trade_id | is_buyer_maker | date | transact_time | interval | diff | |
|---|---|---|---|---|---|---|---|---|---|---|
| 2023-01-27 00:00:00.161 | 1138369 | 2.901 | 54.3 | 3806199 | 3806201 | False | 2023-01-27 00:00:00.161 | 1674777600161 | NaN | 0.001 |
| 2023-01-27 00:00:04.140 | 1138370 | 2.901 | 291.3 | 3806202 | 3806203 | False | 2023-01-27 00:00:04.140 | 1674777604140 | 3979.0 | 0.000 |
| 2023-01-27 00:00:04.339 | 1138373 | 2.902 | 55.1 | 3806205 | 3806207 | False | 2023-01-27 00:00:04.339 | 1674777604339 | 199.0 | 0.001 |
| 2023-01-27 00:00:04.772 | 1138374 | 2.902 | 1032.7 | 3806208 | 3806223 | False | 2023-01-27 00:00:04.772 | 1674777604772 | 433.0 | 0.000 |
| 2023-01-27 00:00:05.562 | 1138375 | 2.901 | 3.5 | 3806224 | 3806224 | False | 2023-01-27 00:00:05.562 | 1674777605562 | 790.0 | 0.000 |
| … | … | … | … | … | … | … | … | … | … | … |
| 2023-01-27 23:59:57.739 | 1544370 | 3.572 | 394.8 | 5074645 | 5074651 | False | 2023-01-27 23:59:57.739 | 1674863997739 | 1224.0 | 0.002 |
| 2023-01-27 23:59:57.902 | 1544372 | 3.573 | 177.6 | 5074652 | 5074655 | False | 2023-01-27 23:59:57.902 | 1674863997902 | 163.0 | 0.001 |
| 2023-01-27 23:59:58.107 | 1544373 | 3.573 | 139.8 | 5074656 | 5074656 | False | 2023-01-27 23:59:58.107 | 1674863998107 | 205.0 | 0.000 |
| 2023-01-27 23:59:58.302 | 1544374 | 3.573 | 60.5 | 5074657 | 5074657 | False | 2023-01-27 23:59:58.302 | 1674863998302 | 195.0 | 0.000 |
| 2023-01-27 23:59:59.894 | 1544376 | 3.571 | 12.1 | 5074662 | 5074664 | False | 2023-01-27 23:59:59.894 | 1674863999894 | 1592.0 | 0.000 |
#1s内的累计分布
depths = np.array(range(0, 3000, 5))
probabilities = np.array([np.mean(df_resampled['quantity'] > depth) for depth in depths])
mean = df_resampled['quantity'].mean()
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2.05)
probabilities_s = np.array([((1+20**(-depth/mean))*depth/mean+1)**(alpha) for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities)
plt.plot(depths, probabilities_s)
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.grid(True)
df_resampled = buy_trades['quantity'].resample('30S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]
depths = np.array(range(0, 12000, 20))
probabilities = np.array([np.mean(df_resampled['quantity'] > depth) for depth in depths])
mean = df_resampled['quantity'].mean()
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2.05)
probabilities_s = np.array([((1+20**(-depth/mean))*depth/mean+1)**(alpha) for depth in depths])
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2)
probabilities_s_2 = np.array([(depth/mean+1)**alpha for depth in depths]) # 无修正
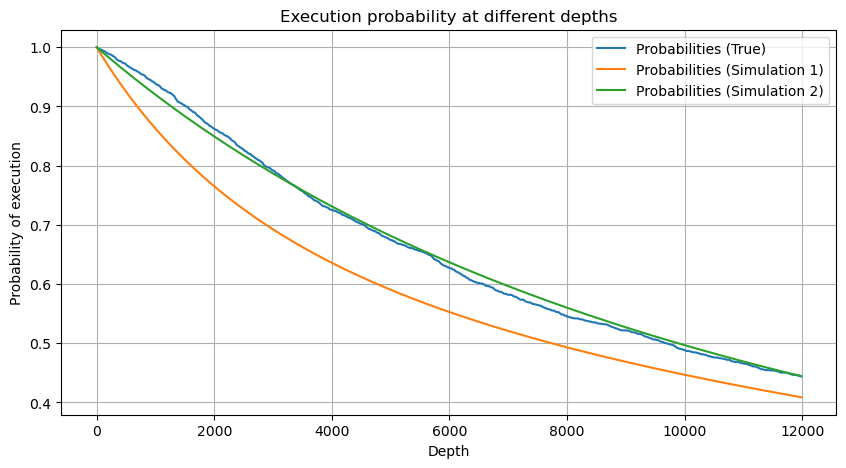
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities,label='Probabilities (True)')
plt.plot(depths, probabilities_s, label='Probabilities (Simulation 1)')
plt.plot(depths, probabilities_s_2, label='Probabilities (Simulation 2)')
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.legend()
plt.grid(True)
Ahora hemos resumido una fórmula general para la distribución del volumen comercial acumulado en diferentes momentos y hemos utilizado la distribución de transacciones individuales para ajustarla, sin tener que contarlas por separado cada vez. Aquí omitimos el proceso y damos la fórmula directamente:
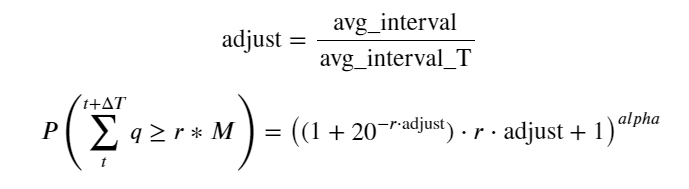
Entre ellos, avg_interval representa el intervalo promedio entre transacciones individuales y avg_interval_T representa el intervalo promedio de los intervalos que se deben estimar. Es un poco confuso. Si queremos estimar el tiempo de transacción de 1 segundo, necesitamos calcular el intervalo promedio entre eventos que contienen transacciones dentro de 1 segundo. Si la probabilidad de que llegue un pedido se ajusta a la distribución de Poisson, debería ser posible estimarla directamente aquí, pero la desviación real es grande, por lo que no la explicaré aquí.
Tenga en cuenta que la probabilidad de que el volumen sea mayor que un cierto valor dentro de un cierto intervalo debe ser bastante diferente de la probabilidad real de la transacción en esa posición en la profundidad, porque cuanto mayor sea el tiempo de espera, mayor será la posibilidad de que el libro de órdenes cambiando, y la transacción también conduce a cambios de profundidad, por lo que la probabilidad de transacción en la misma posición de profundidad cambia en tiempo real a medida que se actualizan los datos.
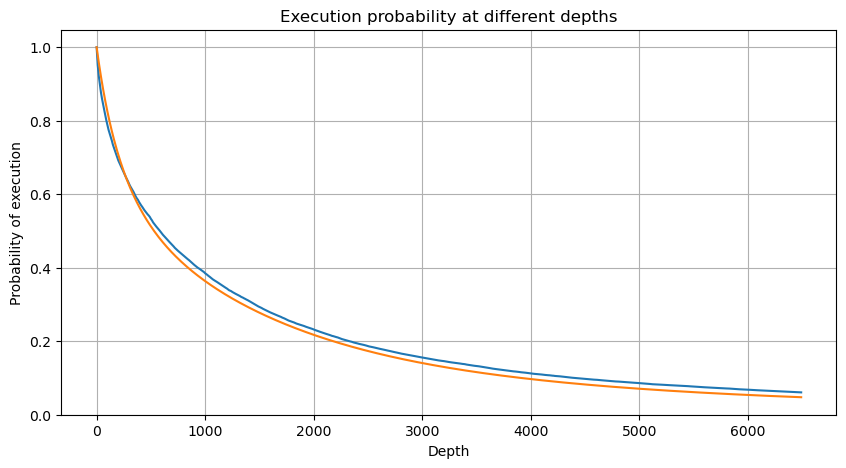
df_resampled = buy_trades['quantity'].resample('2S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]
depths = np.array(range(0, 6500, 10))
probabilities = np.array([np.mean(df_resampled['quantity'] > depth) for depth in depths])
mean = buy_trades['quantity'].mean()
adjust = buy_trades['interval'].mean() / 2620
alpha = np.log(np.mean(buy_trades['quantity'] > mean))/0.7178397931503168
probabilities_s = np.array([((1+20**(-depth*adjust/mean))*depth*adjust/mean+1)**(alpha) for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities)
plt.plot(depths, probabilities_s)
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.grid(True)
Impacto en el precio de una sola transacción
Los datos de transacciones son un tesoro y todavía queda mucho por explorar. Debemos prestar mucha atención al impacto de las órdenes en los precios, lo que afecta la colocación de órdenes pendientes en la estrategia. De manera similar, en función de los datos agregados de transact_time, calcule la diferencia entre el último precio y el primer precio. Si solo hay un pedido, la diferencia es 0. Lo extraño es que todavía hay una pequeña cantidad de resultados de datos con resultados negativos. Esto debería ser un problema con el orden de disposición de los datos, por lo que no lo analizaré aquí.
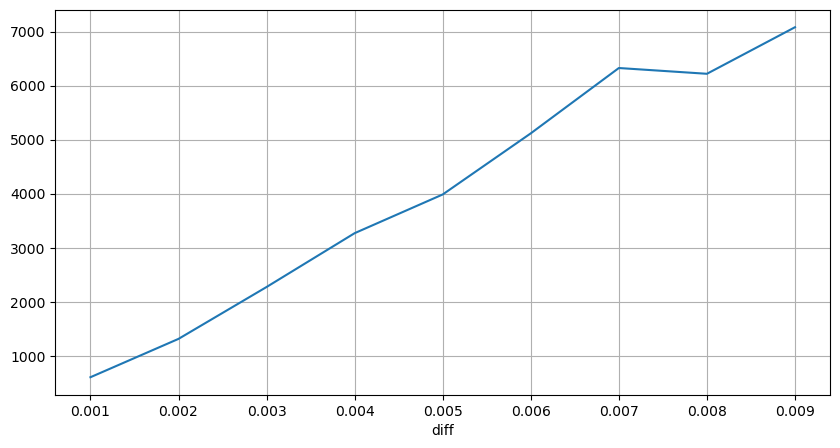
Los resultados muestran que la proporción de ningún impacto es tan alta como 77%, la proporción de 1 tick es 16.5%, 2 ticks es 3.7%, 3 ticks es 1.2% y la proporción de más de 4 ticks es menor a 1%. . Esto básicamente se ajusta a las características de la función exponencial, pero el ajuste no es preciso.
Se contabilizó el volumen de transacciones que causó la diferencia de precio correspondiente y se eliminó la distorsión causada por un impacto demasiado grande. Básicamente se ajusta a la relación lineal, y aproximadamente cada 1000 volúmenes causa una fluctuación de precio de 1 tick. También se puede entender que el número promedio de órdenes pendientes cerca de cada precio es de aproximadamente 1.000.
diff_df = trades[trades['is_buyer_maker']==False].groupby('transact_time')['price'].agg(lambda x: abs(round(x.iloc[-1] - x.iloc[0],3)) if len(x) > 1 else 0)
buy_trades['diff'] = buy_trades['transact_time'].map(diff_df)
diff_counts = buy_trades['diff'].value_counts()
diff_counts[diff_counts>10]/diff_counts.sum()
0.000 0.769965
0.001 0.165527
0.002 0.037826
0.003 0.012546
0.004 0.005986
0.005 0.003173
0.006 0.001964
0.007 0.001036
0.008 0.000795
0.009 0.000474
0.010 0.000227
0.011 0.000187
0.012 0.000087
0.013 0.000080
Name: diff, dtype: float64
diff_group = buy_trades.groupby('diff').agg({
'quantity': 'mean',
'diff': 'last',
})
diff_group['quantity'][diff_group['diff']>0][diff_group['diff']<0.01].plot(figsize=(10,5),grid=True);
Shocks de precios a intervalos regulares
Cuente el impacto del precio en un lapso de 2 segundos. La diferencia aquí es que habrá valores negativos. Por supuesto, dado que aquí solo se cuentan las órdenes de compra, la posición simétrica será un tick más grande. Continúe observando la relación entre el volumen de operaciones y el impacto, y cuente solo los resultados mayores que 0. La conclusión es similar a la de una orden única, que también es una relación lineal aproximada. Cada tick requiere aproximadamente 2000 de volumen.
df_resampled = buy_trades.resample('2S').agg({
'price': ['first', 'last', 'count'],
'quantity': 'sum'
})
df_resampled['price_diff'] = round(df_resampled[('price', 'last')] - df_resampled[('price', 'first')],3)
df_resampled['price_diff'] = df_resampled['price_diff'].fillna(0)
result_df_raw = pd.DataFrame({
'price_diff': df_resampled['price_diff'],
'quantity_sum': df_resampled[('quantity', 'sum')],
'data_count': df_resampled[('price', 'count')]
})
result_df = result_df_raw[result_df_raw['price_diff'] != 0]
result_df['price_diff'][abs(result_df['price_diff'])<0.016].value_counts().sort_index().plot.bar(figsize=(10,5));
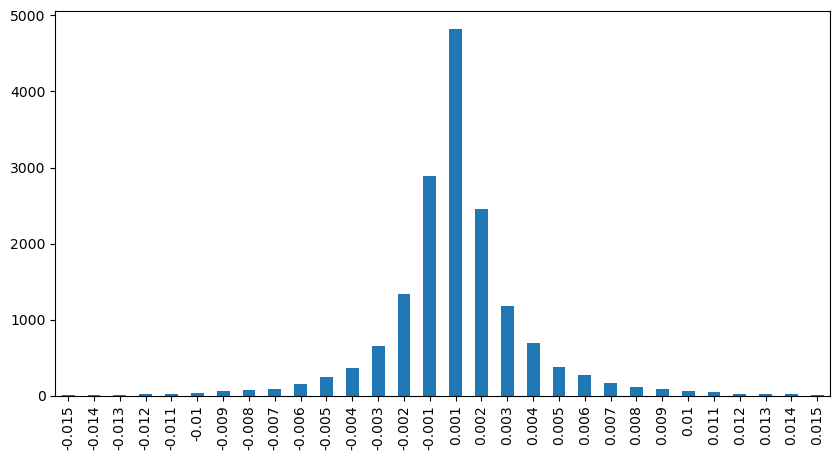
result_df['price_diff'].value_counts()[result_df['price_diff'].value_counts()>30]
0.001 7176
-0.001 3665
0.002 3069
-0.002 1536
0.003 1260
0.004 692
-0.003 608
0.005 391
-0.004 322
0.006 259
-0.005 192
0.007 146
-0.006 112
0.008 82
0.009 75
-0.007 75
-0.008 65
0.010 51
0.011 41
-0.010 31
Name: price_diff, dtype: int64
diff_group = result_df.groupby('price_diff').agg({ 'quantity_sum': 'mean'})
diff_group[(diff_group.index>0) & (diff_group.index<0.015)].plot(figsize=(10,5),grid=True);
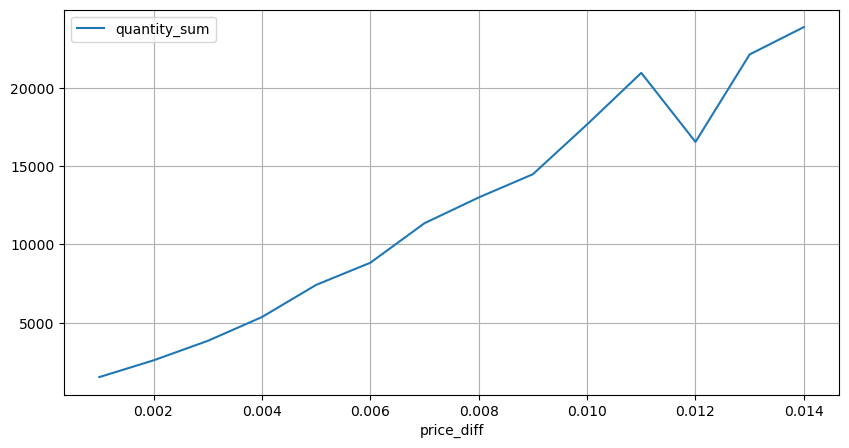
Impacto del volumen en el precio
El volumen necesario para un cambio de marca se calculó anteriormente, pero no es exacto porque se basa en el supuesto de que el impacto ya se ha producido. Ahora veamos el impacto en el precio causado por el volumen comercial.
Los datos aquí se muestrean a 1 segundo, con 100 cantidades como 1 paso, y se cuentan los cambios de precio dentro de este rango de cantidad. Se extrajeron algunas conclusiones valiosas:
- Cuando el volumen de compra es inferior a 500, el cambio de precio esperado es hacia abajo, lo cual es esperado ya que también hay órdenes de venta que afectan el precio.
- Cuando el volumen de negociación es bajo, sigue una relación lineal, es decir, cuanto mayor es el volumen de negociación, mayor es el aumento del precio.
- Cuanto mayor sea el volumen de la orden de compra, mayor será el cambio de precio, lo que a menudo representa una ruptura del precio. Después de la ruptura, el precio puede volver a subir. Junto con el muestreo a intervalos fijos, los datos son inestables.
- Se debe prestar atención a la parte superior del diagrama de dispersión, es decir, la parte donde el volumen corresponde al aumento de precio.
- Solo para este par comercial, se ofrece una versión aproximada de la relación entre el volumen y el cambio de precio:
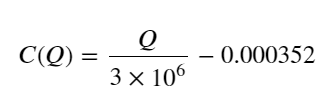
Entre ellos, “C” representa el cambio de precio y “Q” representa el volumen de la orden de compra.
df_resampled = buy_trades.resample('1S').agg({
'price': ['first', 'last', 'count'],
'quantity': 'sum'
})
df_resampled['price_diff'] = round(df_resampled[('price', 'last')] - df_resampled[('price', 'first')],3)
df_resampled['price_diff'] = df_resampled['price_diff'].fillna(0)
result_df_raw = pd.DataFrame({
'price_diff': df_resampled['price_diff'],
'quantity_sum': df_resampled[('quantity', 'sum')],
'data_count': df_resampled[('price', 'count')]
})
result_df = result_df_raw[result_df_raw['price_diff'] != 0]
df = result_df.copy()
bins = np.arange(0, 30000, 100) #
labels = [f'{i}-{i+100-1}' for i in bins[:-1]]
df.loc[:, 'quantity_group'] = pd.cut(df['quantity_sum'], bins=bins, labels=labels)
grouped = df.groupby('quantity_group')['price_diff'].mean()
grouped_df = pd.DataFrame(grouped).reset_index()
grouped_df['quantity_group_center'] = grouped_df['quantity_group'].apply(lambda x: (float(x.split('-')[0]) + float(x.split('-')[1])) / 2)
plt.figure(figsize=(10,5))
plt.scatter(grouped_df['quantity_group_center'], grouped_df['price_diff'],s=10)
plt.plot(grouped_df['quantity_group_center'], np.array(grouped_df['quantity_group_center'].values)/2e6-0.000352,color='red')
plt.xlabel('quantity_group_center')
plt.ylabel('average price_diff')
plt.title('Scatter plot of average price_diff by quantity_group')
plt.grid(True)
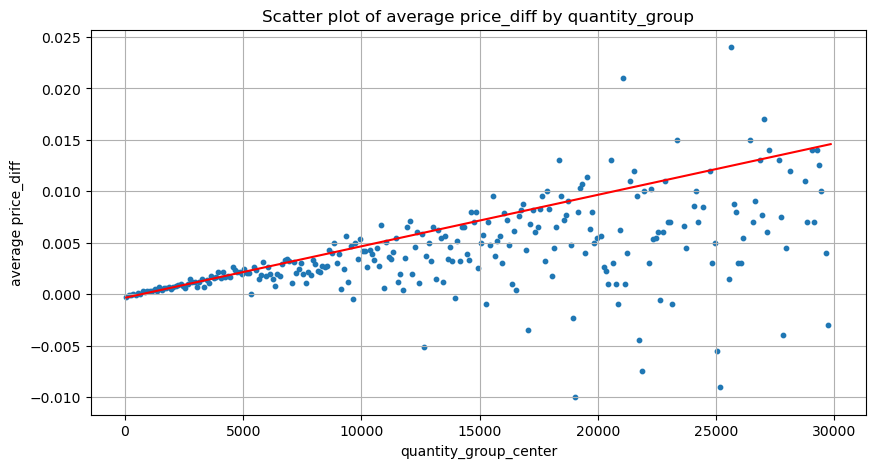
grouped_df.head(10)
| quantity_group | price_diff | quantity_group_center | |
|---|---|---|---|
| 0 | 0-199 | -0.000302 | 99.5 |
| 1 | 100-299 | -0.000124 | 199.5 |
| 2 | 200-399 | -0.000068 | 299.5 |
| 3 | 300-499 | -0.000017 | 399.5 |
| 4 | 400-599 | -0.000048 | 499.5 |
| 5 | 500-699 | 0.000098 | 599.5 |
| 6 | 600-799 | 0.000006 | 699.5 |
| 7 | 700-899 | 0.000261 | 799.5 |
| 8 | 800-999 | 0.000186 | 899.5 |
| 9 | 900-1099 | 0.000299 | 999.5 |
Posición inicial óptima del pedido
Con el modelado del volumen de operaciones y un modelo aproximado del volumen de operaciones correspondiente al impacto del precio, parece que se puede calcular la posición de orden óptima. Hagamos algunas suposiciones y demos una posición de precio óptima irresponsable.
- Supongamos que el precio vuelve a su valor original después del shock (esto, por supuesto, es poco probable y requiere un nuevo análisis de los cambios de precios después del shock).
- Supongamos que la distribución del volumen de operaciones y la frecuencia de órdenes durante este período cumplen con los requisitos preestablecidos (esto también es inexacto, ya que se utiliza el valor de un día para la estimación y las transacciones tienen una agrupación obvia).
- Supongamos que solo se produce una orden de venta durante el tiempo de simulación y luego se cierra la posición.
- Suponiendo que después de ejecutarse la orden, hay otras órdenes de compra que continúan impulsando el precio al alza, especialmente cuando el volumen es muy bajo, este efecto se ignora aquí y simplemente se supone que volverá.
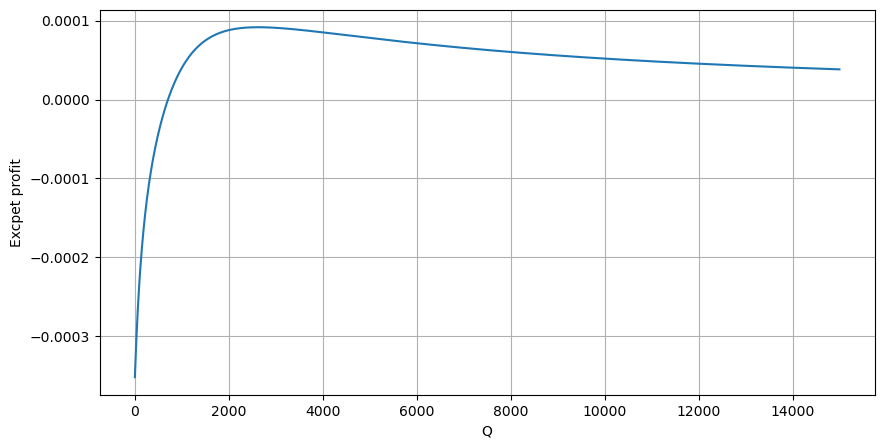
Primero, escriba un rendimiento esperado simple, es decir, la probabilidad de que la orden de compra acumulada sea mayor que Q dentro de 1 segundo, multiplicada por la tasa de rendimiento esperada (es decir, el precio de impacto):
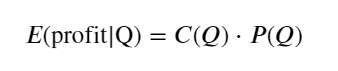
Según el gráfico, el rendimiento esperado es máximo alrededor de 2500, lo que supone aproximadamente 2,5 veces el volumen comercial promedio. Es decir, la orden de venta debe colocarse en 2500. Es necesario enfatizar nuevamente que el eje horizontal representa el volumen comercial en 1 segundo y no puede equipararse simplemente con la posición de profundidad. Y esto ocurre en un momento en el que aún faltan datos profundos muy importantes y solo se basan en especulaciones basadas en transacciones.
Resumir
Se encontró que la distribución del volumen en diferentes intervalos de tiempo es un escalamiento simple de la distribución del volumen de una sola transacción. También hemos elaborado un modelo simple de rentabilidad esperada basado en los shocks de precios y la probabilidad de transacción. Los resultados de este modelo están en línea con nuestras expectativas. Si el volumen de órdenes de venta es pequeño, indica una caída de precios. Se requiere una cierta cantidad para obtener ganancias. márgenes, y cuanto mayor sea el volumen de transacciones, mayor será el margen de beneficio. Cuanto mayor sea la probabilidad, menor será. Existe un tamaño óptimo en el medio, que también es la posición de colocación de órdenes que busca la estrategia. Por supuesto, este modelo sigue siendo demasiado simple. En el próximo artículo seguiré explicándolo en profundidad.
#1s内的累计分布
df_resampled = buy_trades['quantity'].resample('1S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]
depths = np.array(range(0, 15000, 10))
mean = df_resampled['quantity'].mean()
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2.05)
probabilities_s = np.array([((1+20**(-depth/mean))*depth/mean+1)**(alpha) for depth in depths])
profit_s = np.array([depth/2e6-0.000352 for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities_s*profit_s)
plt.xlabel('Q')
plt.ylabel('Excpet profit')
plt.grid(True)