El artículo anterior estudió el intervalo de llegada de pedidos y demostró por qué necesitamos ajustar dinámicamente los parámetros y cómo evaluar la calidad de la estimación. Este artículo se centrará en datos en profundidad y estudiará el precio medio (también llamado precio justo, microprecio, etc.).

Datos de profundidad

Binance proporciona la descarga de datos históricos de las mejores cotizaciones, incluyendo best_bid_price: el mejor precio de oferta, es decir, el precio de oferta máximo, best_bid_qty: el número del mejor precio de oferta, best_ask_price: el mejor precio de venta, best_ask_qty: el número del mejor precio de venta , transaction_time: marca de tiempo. Estos datos no incluyen las órdenes pendientes de segundo nivel y más profundas. La situación del mercado analizada aquí es la de YGG el 7 de agosto. Las fluctuaciones del mercado ese día fueron muy drásticas y la cantidad de datos alcanzó más de 9 millones.

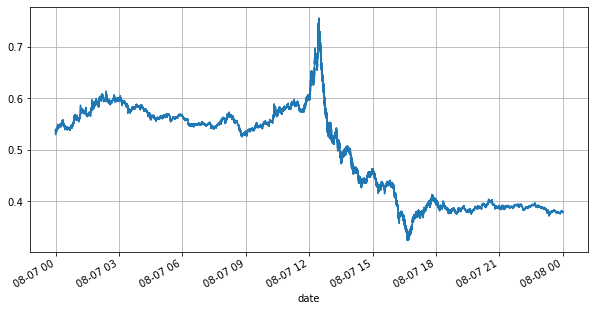
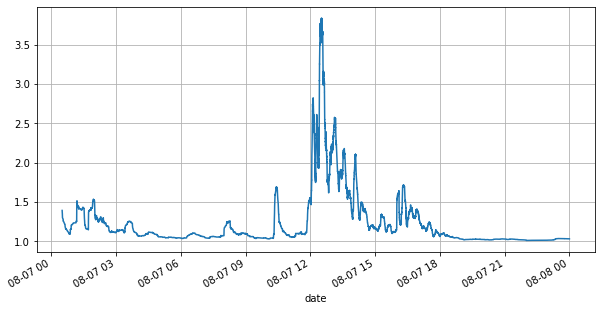
En primer lugar, observemos el mercado del día. Tiene grandes altibajos. Además, el número de órdenes pendientes en el día también ha cambiado mucho con la fluctuación del mercado. En particular, el spread (la diferencia entre el precio y el precio) ha cambiado. El precio de venta y el precio de compra han mostrado significativamente la situación de fluctuación del mercado. Según las estadísticas del mercado de YGG ese día, el 20% de las veces el diferencial era superior a 1 tick. En esta era en la que varios robots compiten en el mercado, esta situación es poco común.

from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

books = pd.read_csv('YGGUSDT-bookTicker-2023-08-07.csv')

tick_size = 0.0001

books['date'] = pd.to_datetime(books['transaction_time'], unit='ms')
books.index = books['date']

books['spread'] = round(books['best_ask_price'] - books['best_bid_price'],4)

books['best_bid_price'][::10].plot(figsize=(10,5),grid=True);

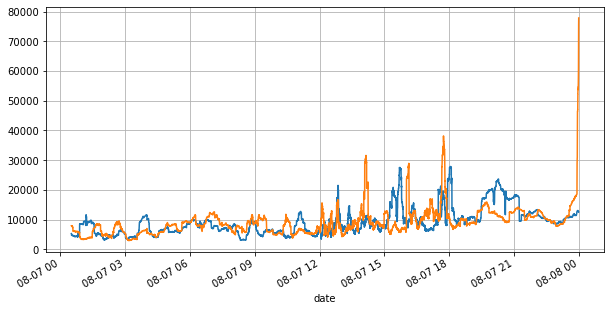
books['best_bid_qty'][::10].rolling(10000).mean().plot(figsize=(10,5),grid=True);
books['best_ask_qty'][::10].rolling(10000).mean().plot(figsize=(10,5),grid=True);

(books['spread'][::10]/tick_size).rolling(10000).mean().plot(figsize=(10,5),grid=True);

books['spread'].value_counts()[books['spread'].value_counts()>500]/books['spread'].value_counts().sum()

0.0001    0.799169
0.0002    0.102750
0.0003    0.042472
0.0004    0.022821
0.0005    0.012792
0.0006    0.007350
0.0007    0.004376
0.0008    0.002712
0.0009    0.001657
0.0010    0.001089
0.0011    0.000740
0.0012    0.000496
0.0013    0.000380
0.0014    0.000258
0.0015    0.000197
0.0016    0.000140
0.0017    0.000112
0.0018    0.000088
0.0019    0.000063
Name: spread, dtype: float64

Citas desequilibradas

De lo anterior se desprende que los volúmenes de órdenes de compra y venta son muy diferentes la mayor parte del tiempo. Esta diferencia tiene un fuerte efecto predictivo sobre las condiciones del mercado a corto plazo. La razón es similar a la mencionada en el artículo anterior: que las pequeñas órdenes de compra a menudo conducen a caídas. Si las órdenes pendientes de un lado son significativamente más pequeñas que las del otro lado, y asumiendo que los volúmenes de órdenes de compra y venta activas son similares, el lado con las órdenes pendientes más pequeñas tendrá más probabilidades de ser absorbido, lo que impulsará el precio. cambios. Las comillas no equilibradas se representan mediante I: 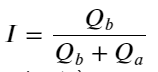Donde Q_b representa la cantidad de la orden de compra (best_bid_qty) y Q_a representa la cantidad de la orden de venta (best_ask_qty).

Definir precio medio: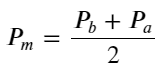

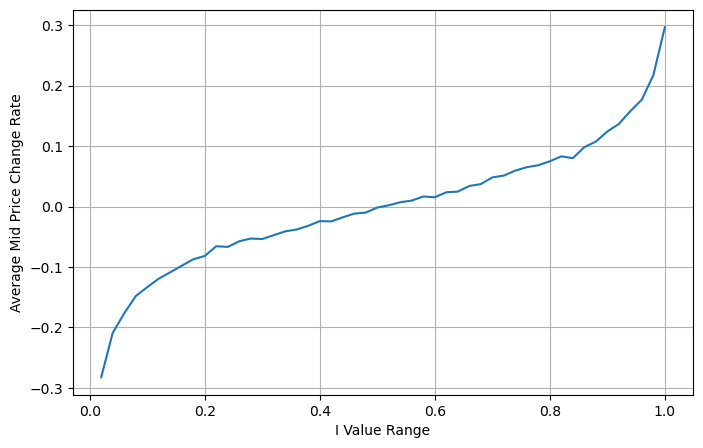
La siguiente figura muestra la relación entre la tasa de cambio del precio medio en el siguiente intervalo y el desequilibrio I. Como se esperaba, a medida que aumenta I, es más probable que el precio suba y cuanto más cerca esté de 1, mayor será la magnitud del desequilibrio. El cambio de precios también se acelera. En el trading de alta frecuencia, el objetivo de introducir el precio medio es predecir mejor los cambios futuros de precios. En otras palabras, cuanto menor sea la diferencia con el precio futuro, mejor se define el precio medio. Obviamente, el desequilibrio de órdenes pendientes aporta información adicional para la predicción de la estrategia. Teniendo esto en cuenta, definimos el precio medio ponderado:

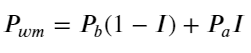
books['I'] = books['best_bid_qty'] / (books['best_bid_qty'] + books['best_ask_qty'])

books['mid_price'] = (books['best_ask_price'] + books['best_bid_price'])/2

bins = np.linspace(0, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['price_change'] = (books['mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['price_change'].mean()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Average Mid Price Change Rate');
plt.grid(True)

books['weighted_mid_price'] = books['mid_price'] + books['spread']*books['I']/2
bins = np.linspace(-1, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['weighted_price_change'] = (books['weighted_mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['weighted_price_change'].mean()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Weighted Average Mid Price Change Rate');
plt.grid(True)

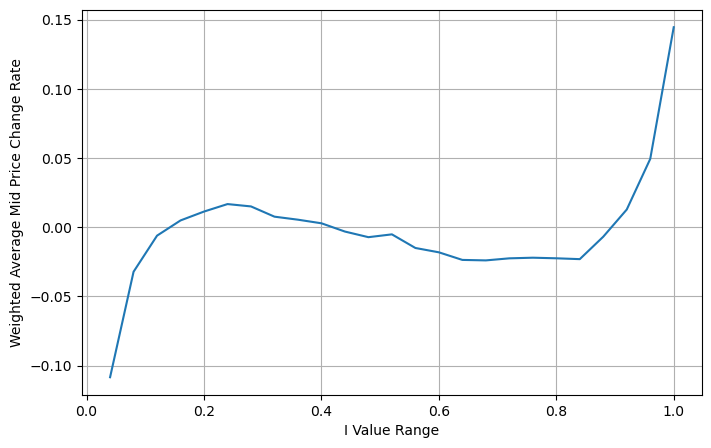
Ajuste del precio medio ponderado

De la figura se desprende que el precio medio ponderado cambia mucho menos que los diferentes I, lo que significa que el precio medio ponderado se ajusta mejor. Pero todavía hay algunas regularidades, como alrededor de 0,2 y 0,8, donde las desviaciones son relativamente grandes. Esto demuestra que todavía puedo aportar información adicional. Como el precio medio ponderado supone que el término de corrección de precio es completamente lineal con I, esto obviamente no es cierto. Como se puede ver en la figura anterior, cuando I está cerca de 0 y 1, la desviación es más rápida y no es una relación lineal.

Para una mirada más intuitiva, I se redefine aquí:

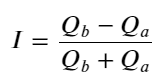
En este momento:

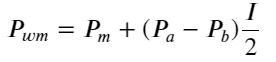
Observando esta forma, podemos encontrar que el precio medio ponderado es una corrección del precio medio promedio. El coeficiente del término de corrección es Spread, y el término de corrección es una función de I. El precio medio ponderado simplemente supone que Esta relación es I/2. En este momento se refleja la ventaja de la distribución ajustada de I (-1,1). I es simétrica respecto del origen, lo que nos permite encontrar la relación de ajuste de la función. Observa la gráfica, esta función debe satisfacer la relación de potencia impar de I, lo cual es consistente con el rápido crecimiento de ambos lados y la simetría respecto del origen. Además, se puede observar que el valor cerca del origen es cercano a lineal, y cuando I es 0, el resultado de la función es 0, y cuando I es 1, el resultado de la función es 0,5. Entonces supongo que esta función se verá así:

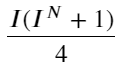
Aquí N es un número par positivo. Después de una prueba real, es mejor que N sea 8. Hasta ahora, este artículo propone un precio medio ponderado revisado:

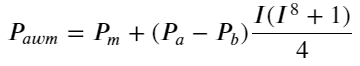
En este punto, el cambio en el precio medio previsto básicamente no tiene nada que ver con I. Aunque este resultado es mejor que el precio medio ponderado simple, no se puede aplicar en operaciones reales. Es solo una idea que se da aquí. Un artículo de 2017 de S Stoikov presentó el método de la cadena de MarkovMicro-Price, y te da el código relevante, también puedes estudiarlo.

books['I'] = (books['best_bid_qty'] - books['best_ask_qty']) / (books['best_bid_qty'] + books['best_ask_qty'])

books['weighted_mid_price'] = books['mid_price'] + books['spread']*books['I']/2
bins = np.linspace(-1, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['weighted_price_change'] = (books['weighted_mid_price'].pct_change()/tick_size).shift(-1)
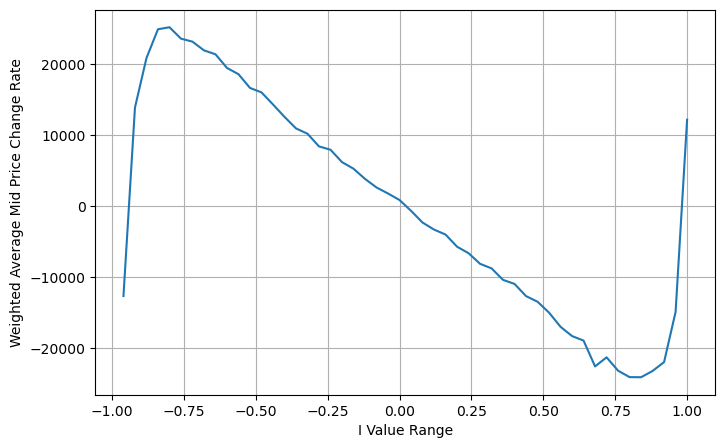
avg_change = books.groupby('I_bins')['weighted_price_change'].sum()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Weighted Average Mid Price Change Rate');
plt.grid(True)

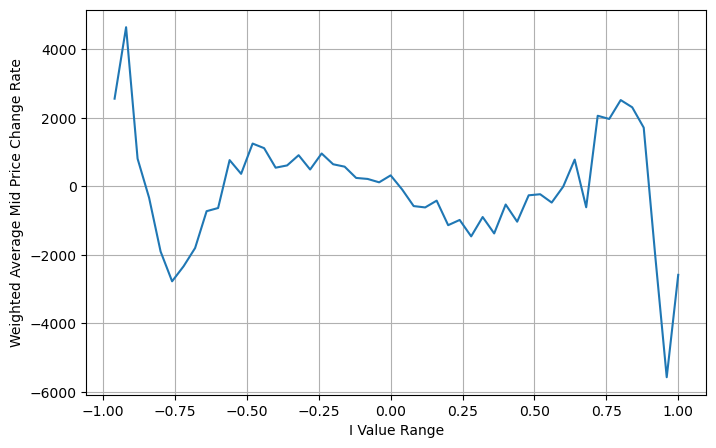
books['adjust_mid_price'] = books['mid_price'] + books['spread']*(books['I'])*(books['I']**8+1)/4
bins = np.linspace(-1, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['adjust_mid_price'] = (books['adjust_mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['adjust_mid_price'].sum()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Weighted Average Mid Price Change Rate');
plt.grid(True)

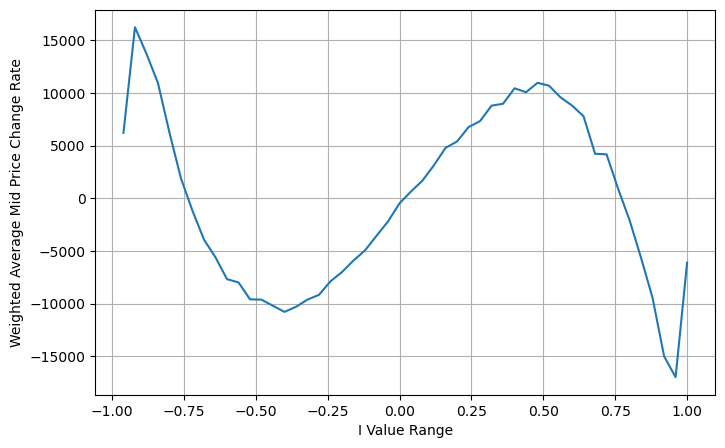
books['adjust_mid_price'] = books['mid_price'] + books['spread']*(books['I']**3)/2
bins = np.linspace(-1, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['adjust_mid_price'] = (books['adjust_mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['adjust_mid_price'].sum()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Weighted Average Mid Price Change Rate');
plt.grid(True)

Resumir

El precio medio es muy importante para las estrategias de alta frecuencia. Es una predicción de los precios futuros a corto plazo, por lo que el precio medio debe ser lo más preciso posible. Los precios medios introducidos anteriormente se basan en datos de mercado, porque solo se utiliza un precio de mercado en el análisis. En el comercio real, la estrategia debe utilizar todos los datos tanto como sea posible, especialmente cuando hay intercambios comerciales en el comercio real, y la predicción del precio medio debe probarse con el precio de transacción real. Recuerdo que Stoikov aparentemente publicó un tweet en el que decía que el precio medio real debería ser el promedio ponderado de la probabilidad de una transacción de compra-venta. Esta cuestión ya se estudió en el artículo anterior. Debido al espacio limitado, estos temas se tratarán en detalle en el próximo artículo.