Estrategia de media móvil adaptativa de canal gaussiano
Descripción general
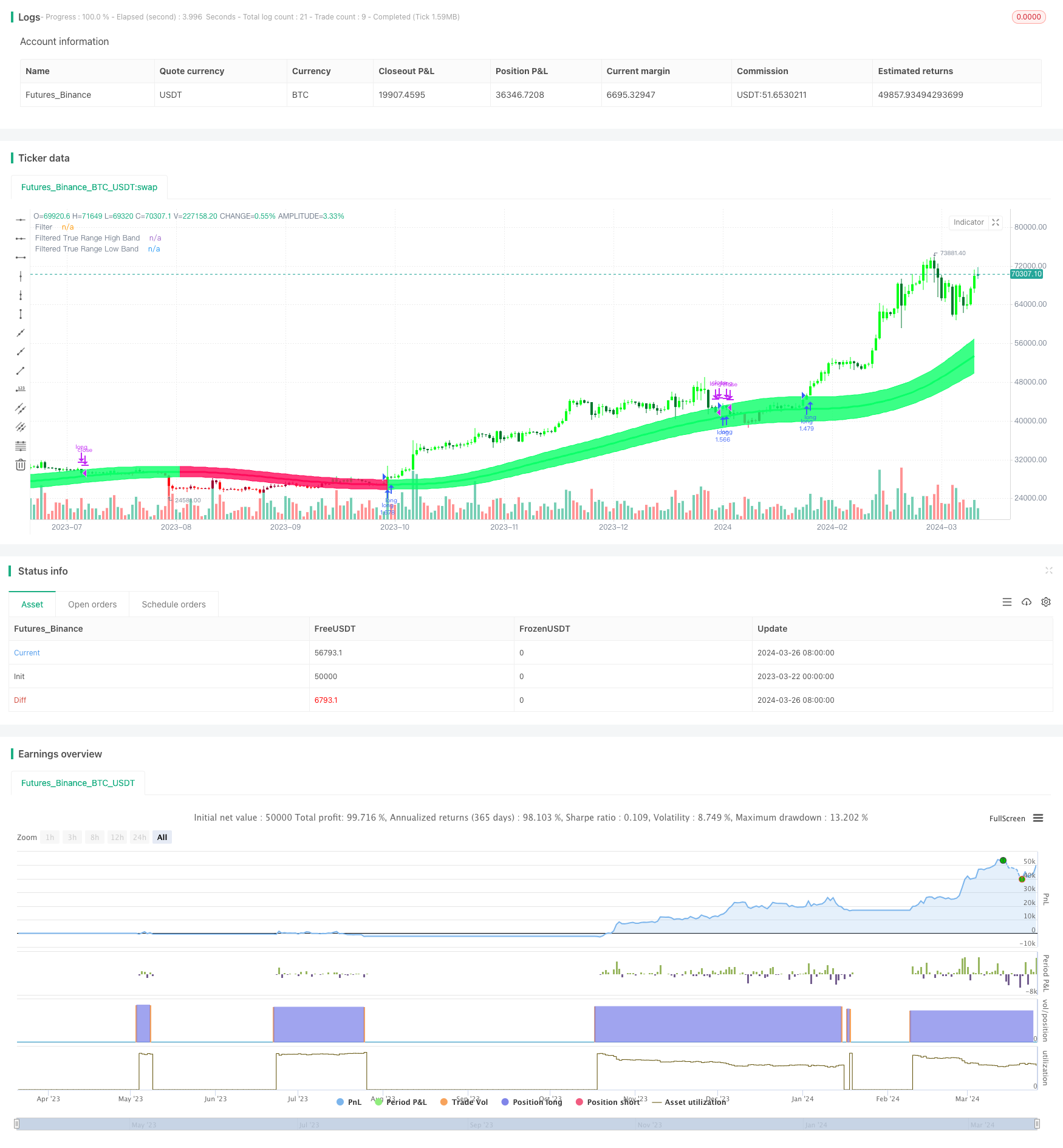
La estrategia de Gauss Channel Adapted Equilibrium es una estrategia de negociación cuantitativa que utiliza la técnica de Gauss Wave y la configuración de parámetros adaptados. La estrategia se basa en la teoría de Gauss Wave, propuesta por John Ehlers, para generar una señal de negociación suave y adaptable mediante el cálculo de una media móvil de índices múltiples sobre los datos de precios.
Principio de estrategia
El principio de la estrategia de adaptación de la vía de Gauss es el siguiente:
- Calcular el valor de las ondas de Gauss del precio. Calcular los parámetros Beta y Alpha según el ciclo de muestreo y el número de puntos polares configurados por el usuario, y luego escalar las ondas de Gauss sobre los datos de precios para obtener una secuencia de precios suavizada.
- Calcula el valor de Gauss de la amplitud real de las fluctuaciones. El mismo tratamiento de Gauss de la amplitud real de los precios obtiene una secuencia de amplitud de fluctuaciones suave.
- Construir un canal de Gauss. El precio después de la onda de Gauss es el medio de la vía, el medio de la vía de la vía superior se suma a la amplitud real de la oscilación multiplicada por el número de veces que el usuario establece, el medio de la vía inferior se reduce a este valor, formando un canal dinámico.
- Genera señales de negociación. Cuando el precio se eleva por encima de la vía, genera una señal de compra; cuando el precio baja por debajo de la vía, genera una señal de venta.
- Introducción de un parámetro de intervalo de tiempo. El usuario puede configurar el inicio y el final de la ejecución de la estrategia, durante el cual la estrategia se ejecutará según la señal de negociación.
Análisis de las ventajas
La estrategia de adaptación equitativa de Gauss tiene las siguientes ventajas:
- La estrategia adopta parámetros de ajuste dinámico, que se pueden adaptar a diferentes estados de mercado y variedades de transacciones, sin necesidad de una puesta en marcha manual frecuente.
- El seguimiento de tendencias es bueno. Al construir canales de precios, las estrategias pueden capturar y seguir mejor las tendencias del mercado, evitando de manera efectiva las falsas señales en mercados convulsionados.
- Es suavizante. Utiliza la técnica de las ondas de Gauss para procesar los datos de precios de manera suave, eliminando la mayor parte del ruido del mercado y haciendo que las señales de negociación sean más fiables.
- Alta flexibilidad. El usuario puede ajustar los parámetros de la estrategia según sea necesario, como el ciclo de muestreo, el número de puntos polares, el múltiplo de oscilación, etc., para optimizar el rendimiento de la estrategia.
- La introducción de los parámetros de período de tiempo permite que las estrategias se ejecuten en un rango de tiempo especificado, lo que facilita la aplicación en el campo y el estudio retrospectivo.
Análisis de riesgos
A pesar de las ventajas de la estrategia de adaptación de la vía de Gauss, existen algunos riesgos:
- Riesgo de configuración de parámetros: la configuración inadecuada de los parámetros puede provocar el fracaso o el mal desempeño de las estrategias, por lo que es necesario realizar pruebas y optimizaciones repetidas en aplicaciones reales.
- Riesgo de emergencia. La estrategia puede no reaccionar correctamente a tiempo ante algunos eventos de gran importancia, lo que puede causar pérdidas.
- Riesgo de sobreajuste. Si los parámetros se ajustan demasiado a los datos históricos, puede ocasionar un mal desempeño de la estrategia en el futuro, que requiere tener en cuenta el desempeño interno y externo de la muestra.
- La estrategia se aplica principalmente a los mercados de tendencia, donde el riesgo de arbitraje puede ser mayor si se opera con frecuencia en mercados convulsivos.
Dirección de optimización
Las direcciones de optimización de la estrategia de adaptación de la vía de Gauss incluyen:
- Optimización de parámetros dinámicos. Optimización automática y ajuste dinámico de los parámetros de la estrategia mediante la introducción de tecnologías como el aprendizaje automático, para mejorar la adaptabilidad.
- La fusión multifactorial consiste en la combinación de otros indicadores o factores técnicos efectivos con el canal de Gauss para formar una señal de negociación más sólida.
- Optimización de la gestión de posiciones. Adición de reglas razonables de gestión de posiciones y administración de fondos en la base de la estrategia, control de retiros y riesgos.
- Multi-variedades de colaboración. Extensión de la estrategia a varias variedades de operaciones diferentes para dispersar el riesgo a través de la asignación de activos y el análisis de correlación.
Resumir
La estrategia de la línea de equilibrio autoadaptativa del canal de Gauss es una estrategia de negociación cuantitativa basada en las ondas de Gauss y los parámetros de adaptación para generar una señal de negociación fluida y confiable mediante la construcción dinámica de un canal de precios. La estrategia tiene ventajas como una gran adaptabilidad, un buen seguimiento de tendencias, una gran flexibilidad, gran flexibilidad y gran utilidad, pero también enfrenta riesgos futuros como la configuración de parámetros, eventos inesperados, exceso de adaptación y arbitraje.
/*backtest
start: 2023-03-22 00:00:00
end: 2024-03-27 00:00:00
period: 1d
basePeriod: 1h
exchanges: [{"eid":"Futures_Binance","currency":"BTC_USDT"}]
*/
//@version=4
strategy(title="Gaussian Channel Strategy v1.0", overlay=true, calc_on_every_tick=false, initial_capital=10000, default_qty_type=strategy.percent_of_equity, default_qty_value=100, commission_type=strategy.commission.percent, commission_value=0.1)
// Date condition inputs
startDate = input(title="Date Start", type=input.time, defval=timestamp("1 Jan 2018 00:00 +0000"), group="Dates")
endDate = input(title="Date End", type=input.time, defval=timestamp("31 Dec 2060 23:59 +0000"), group="Dates")
timeCondition = true
// This study is an experiment utilizing the Ehlers Gaussian Filter technique combined with lag reduction techniques and true range to analyze trend activity.
// Gaussian filters, as Ehlers explains it, are simply exponential moving averages applied multiple times.
// First, beta and alpha are calculated based on the sampling period and number of poles specified. The maximum number of poles available in this script is 9.
// Next, the data being analyzed is given a truncation option for reduced lag, which can be enabled with "Reduced Lag Mode".
// Then the alpha and source values are used to calculate the filter and filtered true range of the dataset.
// Filtered true range with a specified multiplier is then added to and subtracted from the filter, generating a channel.
// Lastly, a one pole filter with a N pole alpha is averaged with the filter to generate a faster filter, which can be enabled with "Fast Response Mode".
//Custom bar colors are included.
//Note: Both the sampling period and number of poles directly affect how much lag the indicator has, and how smooth the output is.
// Larger inputs will result in smoother outputs with increased lag, and smaller inputs will have noisier outputs with reduced lag.
// For the best results, I recommend not setting the sampling period any lower than the number of poles + 1. Going lower truncates the equation.
//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
//Updates:
// Huge shoutout to @e2e4mfck for taking the time to improve the calculation method!
// -> migrated to v4
// -> pi is now calculated using trig identities rather than being explicitly defined.
// -> The filter calculations are now organized into functions rather than being individually defined.
// -> Revamped color scheme.
//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
//Functions - courtesy of @e2e4mfck
//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
//Filter function
f_filt9x (_a, _s, _i) =>
int _m2 = 0, int _m3 = 0, int _m4 = 0, int _m5 = 0, int _m6 = 0,
int _m7 = 0, int _m8 = 0, int _m9 = 0, float _f = .0, _x = (1 - _a)
// Weights.
// Initial weight _m1 is a pole number and equal to _i
_m2 := _i == 9 ? 36 : _i == 8 ? 28 : _i == 7 ? 21 : _i == 6 ? 15 : _i == 5 ? 10 : _i == 4 ? 6 : _i == 3 ? 3 : _i == 2 ? 1 : 0
_m3 := _i == 9 ? 84 : _i == 8 ? 56 : _i == 7 ? 35 : _i == 6 ? 20 : _i == 5 ? 10 : _i == 4 ? 4 : _i == 3 ? 1 : 0
_m4 := _i == 9 ? 126 : _i == 8 ? 70 : _i == 7 ? 35 : _i == 6 ? 15 : _i == 5 ? 5 : _i == 4 ? 1 : 0
_m5 := _i == 9 ? 126 : _i == 8 ? 56 : _i == 7 ? 21 : _i == 6 ? 6 : _i == 5 ? 1 : 0
_m6 := _i == 9 ? 84 : _i == 8 ? 28 : _i == 7 ? 7 : _i == 6 ? 1 : 0
_m7 := _i == 9 ? 36 : _i == 8 ? 8 : _i == 7 ? 1 : 0
_m8 := _i == 9 ? 9 : _i == 8 ? 1 : 0
_m9 := _i == 9 ? 1 : 0
// filter
_f := pow(_a, _i) * nz(_s) +
_i * _x * nz(_f[1]) - (_i >= 2 ?
_m2 * pow(_x, 2) * nz(_f[2]) : 0) + (_i >= 3 ?
_m3 * pow(_x, 3) * nz(_f[3]) : 0) - (_i >= 4 ?
_m4 * pow(_x, 4) * nz(_f[4]) : 0) + (_i >= 5 ?
_m5 * pow(_x, 5) * nz(_f[5]) : 0) - (_i >= 6 ?
_m6 * pow(_x, 6) * nz(_f[6]) : 0) + (_i >= 7 ?
_m7 * pow(_x, 7) * nz(_f[7]) : 0) - (_i >= 8 ?
_m8 * pow(_x, 8) * nz(_f[8]) : 0) + (_i == 9 ?
_m9 * pow(_x, 9) * nz(_f[9]) : 0)
//9 var declaration fun
f_pole (_a, _s, _i) =>
_f1 = f_filt9x(_a, _s, 1), _f2 = (_i >= 2 ? f_filt9x(_a, _s, 2) : 0), _f3 = (_i >= 3 ? f_filt9x(_a, _s, 3) : 0)
_f4 = (_i >= 4 ? f_filt9x(_a, _s, 4) : 0), _f5 = (_i >= 5 ? f_filt9x(_a, _s, 5) : 0), _f6 = (_i >= 6 ? f_filt9x(_a, _s, 6) : 0)
_f7 = (_i >= 2 ? f_filt9x(_a, _s, 7) : 0), _f8 = (_i >= 8 ? f_filt9x(_a, _s, 8) : 0), _f9 = (_i == 9 ? f_filt9x(_a, _s, 9) : 0)
_fn = _i == 1 ? _f1 : _i == 2 ? _f2 : _i == 3 ? _f3 :
_i == 4 ? _f4 : _i == 5 ? _f5 : _i == 6 ? _f6 :
_i == 7 ? _f7 : _i == 8 ? _f8 : _i == 9 ? _f9 : na
[_fn, _f1]
//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
//Inputs
//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
//Source
src = input(defval=hlc3, title="Source")
//Poles
int N = input(defval=4, title="Poles", minval=1, maxval=9)
//Period
int per = input(defval=144, title="Sampling Period", minval=2)
//True Range Multiplier
float mult = input(defval=1.414, title="Filtered True Range Multiplier", minval=0)
//Lag Reduction
bool modeLag = input(defval=false, title="Reduced Lag Mode")
bool modeFast = input(defval=false, title="Fast Response Mode")
//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
//Definitions
//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
//Beta and Alpha Components
beta = (1 - cos(4*asin(1)/per)) / (pow(1.414, 2/N) - 1)
alpha = - beta + sqrt(pow(beta, 2) + 2*beta)
//Lag
lag = (per - 1)/(2*N)
//Data
srcdata = modeLag ? src + (src - src[lag]) : src
trdata = modeLag ? tr(true) + (tr(true) - tr(true)[lag]) : tr(true)
//Filtered Values
[filtn, filt1] = f_pole(alpha, srcdata, N)
[filtntr, filt1tr] = f_pole(alpha, trdata, N)
//Lag Reduction
filt = modeFast ? (filtn + filt1)/2 : filtn
filttr = modeFast ? (filtntr + filt1tr)/2 : filtntr
//Bands
hband = filt + filttr*mult
lband = filt - filttr*mult
// Colors
color1 = #0aff68
color2 = #00752d
color3 = #ff0a5a
color4 = #990032
fcolor = filt > filt[1] ? #0aff68 : filt < filt[1] ? #ff0a5a : #cccccc
barcolor = (src > src[1]) and (src > filt) and (src < hband) ? #0aff68 : (src > src[1]) and (src >= hband) ? #0aff1b : (src <= src[1]) and (src > filt) ? #00752d :
(src < src[1]) and (src < filt) and (src > lband) ? #ff0a5a : (src < src[1]) and (src <= lband) ? #ff0a11 : (src >= src[1]) and (src < filt) ? #990032 : #cccccc
//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
//Outputs
//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
//Filter Plot
filtplot = plot(filt, title="Filter", color=fcolor, linewidth=3)
//Band Plots
hbandplot = plot(hband, title="Filtered True Range High Band", color=fcolor)
lbandplot = plot(lband, title="Filtered True Range Low Band", color=fcolor)
//Channel Fill
fill(hbandplot, lbandplot, title="Channel Fill", color=fcolor, transp=80)
//Bar Color
barcolor(barcolor)
longCondition = crossover(close, hband) and timeCondition
closeAllCondition = crossunder(close, hband) and timeCondition
if longCondition
strategy.entry("long", strategy.long)
if closeAllCondition
strategy.close("long")