Estrategia de pronóstico de series temporales AR-GARCH
¿Por qué el análisis técnico tradicional no funciona en un mercado complejo?
En el campo de las operaciones cuantitativas, a menudo nos encontramos con esta confusión: ¿por qué las estrategias basadas en las medias móviles simples o RSI funcionan mejor en ciertos entornos de mercado, pero fallan con frecuencia en otros? La respuesta reside en la complejidad de las series de tiempo financieras, que no solo tienen una correlación entre sí, sino que también presentan características de fluctuación temporal.
La estrategia que analizaremos hoy, que combina hábilmente el modelo de regresión automática AR(2) y el modelo de diferenciación condicional GARCH(1,1), trata de resolver este problema desde un punto de vista estadístico. No se trata de una simple superposición de indicadores técnicos, sino de una excavación en profundidad de las características esenciales de la secuencia de tiempo financiera.
¿Cómo captura el modelo el efecto memoria del precio?
El núcleo de la estrategia está en la aplicación del modelo de autorregresividad AR[2]: ¿Qué es la autorregresividad? En pocas palabras, es usar el yo pasado para predecir el yo futuro.[3] El modelo de AR[2] supone que la tasa de rendimiento actual puede ser representada linealmente por la tasa de rendimiento de los dos períodos anteriores:
r_t = φ₁ × r_{t-1} + φ₂ × r_{t-2} + ε_t
En el código se resuelven los coeficientes φ1 y φ2 a través de la ecuación de Yule-Walker:
c0 = calcAutoCovariance(returns, 0, lengthReg) // 滞后0期自协方差
c1 = calcAutoCovariance(returns, 1, lengthReg) // 滞后1期自协方差
c2 = calcAutoCovariance(returns, 2, lengthReg) // 滞后2期自协方差
phi1 = (c1 * c0 - c2 * c1) / denominator // 第一个自回归系数
phi2 = (c2 * c0 - c1 * c1) / denominator // 第二个自回归系数
La ventaja de este método es que no se basa en el juicio subjetivo, sino que deja que los datos hablen por sí mismos y descubre la regularidad implícita en la secuencia de precios.
¿Por qué el modelo GARCH es mejor para representar el riesgo de mercado?
Los modelos AR no son suficientes, ya que la volatilidad de los mercados financieros no es constante. Todos sabemos que los fenómenos de “concentración de la volatilidad” son grandes fluctuaciones que a menudo son acompañadas de grandes fluctuaciones, y las épocas de calma suelen durar más tiempo.
El modelo GARCH ((1,1) fue diseñado para representar esta característica:
σ²_t = ω + α × ε²_{t-1} + β × σ²_{t-1}
La lógica de implementación en el código refleja esto claramente:
omega = (1 - adjustedAlpha - adjustedBeta) * longTermVar
garchVariance := omega + adjustedAlpha * math.pow(arResidual[1], 2) + adjustedBeta * garchVariance[1]
La clave aquí es que la diferencia entre las condiciones actuales depende no sólo del residuo cuadrado de la diferencia anterior (impacto a corto plazo) sino también de la diferencia entre las condiciones anteriores (persistencia a largo plazo). El parámetro α controla el impacto de los impactos a corto plazo y β controla la persistencia de la tasa de fluctuación.
¿Cómo la lógica de negociación de la estrategia equilibra el riesgo y la ganancia?
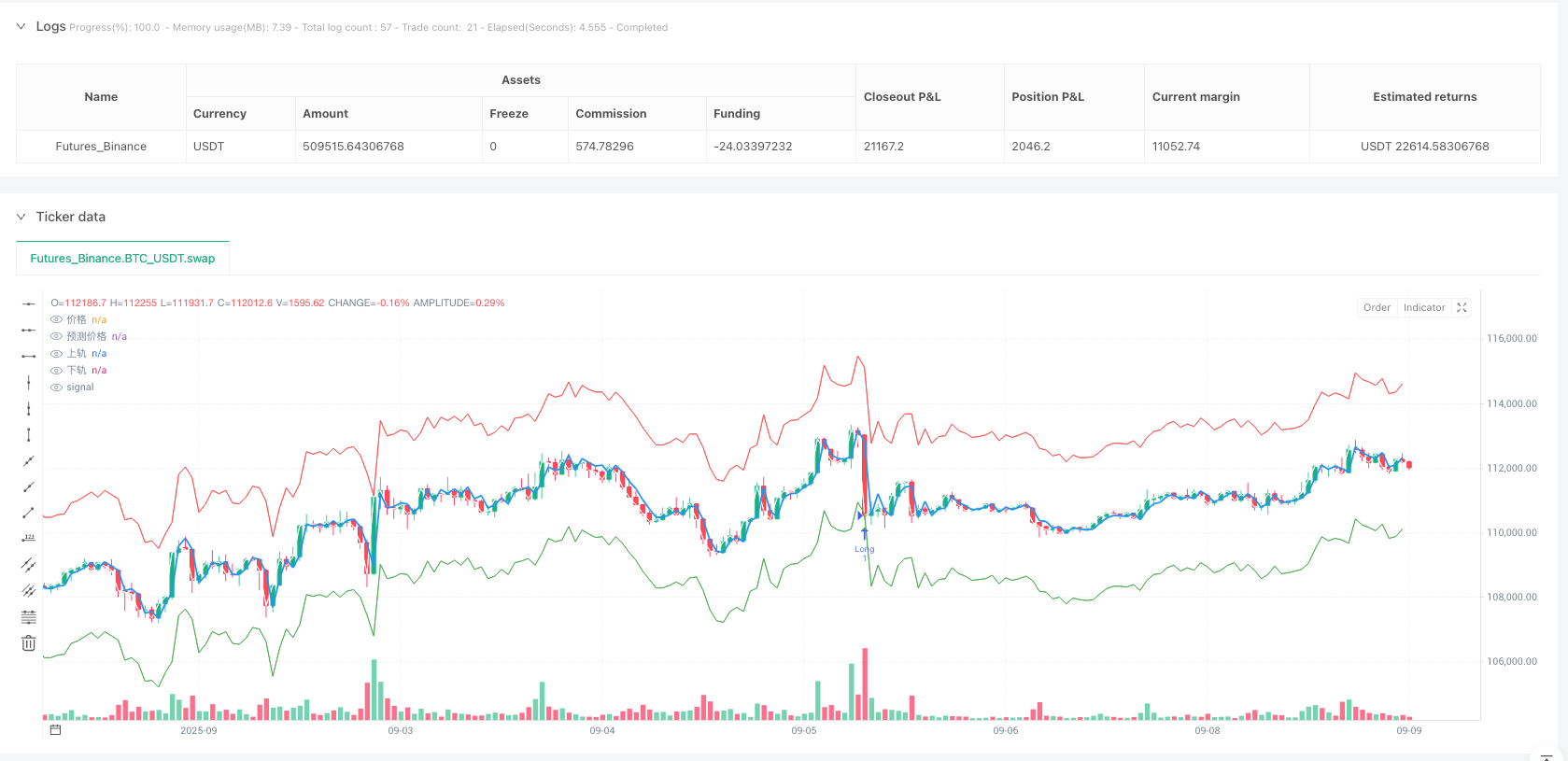
La estrategia construye un intervalo de confianza dinámico con las predicciones de AR y las estimaciones de fluctuaciones de GARCH:
upperReturnBand = arReturnPredict + stdevFactor * garchStd
lowerReturnBand = arReturnPredict - stdevFactor * garchStd
La lógica de generación de la señal de negociación refleja la idea de la regresión a la media:
- Si el precio se desvía hacia abajo, entonces el precio se desvía hacia abajo.
- Cuando el precio se desvía por la banda superior (shortSignal = rawPrice > upperPriceBand)
El truco de este diseño es que el ancho del intervalo de confianza se ajusta a la dinámica de la volatilidad del mercado. En períodos de alta volatilidad, el intervalo se amplía, reduciendo la frecuencia de negociación; en períodos de baja volatilidad, el intervalo se estrecha, aumentando las oportunidades de negociación.
¿Cuáles son las cuestiones clave a las que hay que prestar atención en la aplicación práctica?
1. Pruebas de estabilidad del modelo El código incluye importantes comprobaciones de estabilidad:
if stabilityCheck >= 0.99 or math.abs(phi2) >= 0.99
scaleFactor = 0.95 / math.max(stabilityCheck, math.abs(phi2) + 0.01)
Esto asegura la estabilidad de los modelos AR y evita resultados dispersivos.
2. Restricción de convergencia de parámetros El modelo GARCH requiere que α + β < 1 para garantizar la existencia de diferencias a largo plazo:
if sumParam >= 0.999
scale = 0.99 / sumParam
3. La necesidad de un mecanismo de filtración Las estrategias ofrecen opciones de filtración de RSI, lo cual es importante en aplicaciones reales. Los modelos puramente estadísticos pueden ignorar las características tendenciales del mercado, y la inclusión de indicadores técnicos puede proporcionar señales de confirmación adicionales.
Limitaciones de la estrategia y mejoras
A pesar de que esta estrategia es muy elegante en teoría, en la práctica se debe tener en cuenta:
Opciones de frecuencia de datosEl modelo AR-GARCH presenta una gran variación en el rendimiento en diferentes períodos. Los datos de alta frecuencia proporcionan más información, pero también introducen más ruido.
Variabilidad temporal de los parámetrosEn la implementación actual, se supone que los parámetros AR y GARCH son constantes en la ventana de estimación, pero la estructura real del mercado puede cambiar.
Impacto en el costo de las transaccionesLas estrategias de arbitraje estadístico generalmente requieren una mayor frecuencia de transacciones, y las comisiones y los costos de los puntos de deslizamiento no pueden ser ignorados.
Conclusión: El valor de la modelación estadística en las transacciones cuantitativas
Esta estrategia AR-GARCH muestra el poder de la estadística moderna en la modelación financiera. No es una simple combinación de indicadores técnicos, sino una excavación profunda de las características estadísticas de la secuencia de tiempo financiera.
Para los operadores cuantitativos, el valor de entender este tipo de estrategias no solo radica en su aplicación directa, sino también en la capacidad de analizar el mercado con una mentalidad estadística. Hoy en día, en la era de la IA y el aprendizaje automático, estos modelos estadísticos clásicos siguen siendo una piedra angular importante para entender los mercados y construir estrategias.
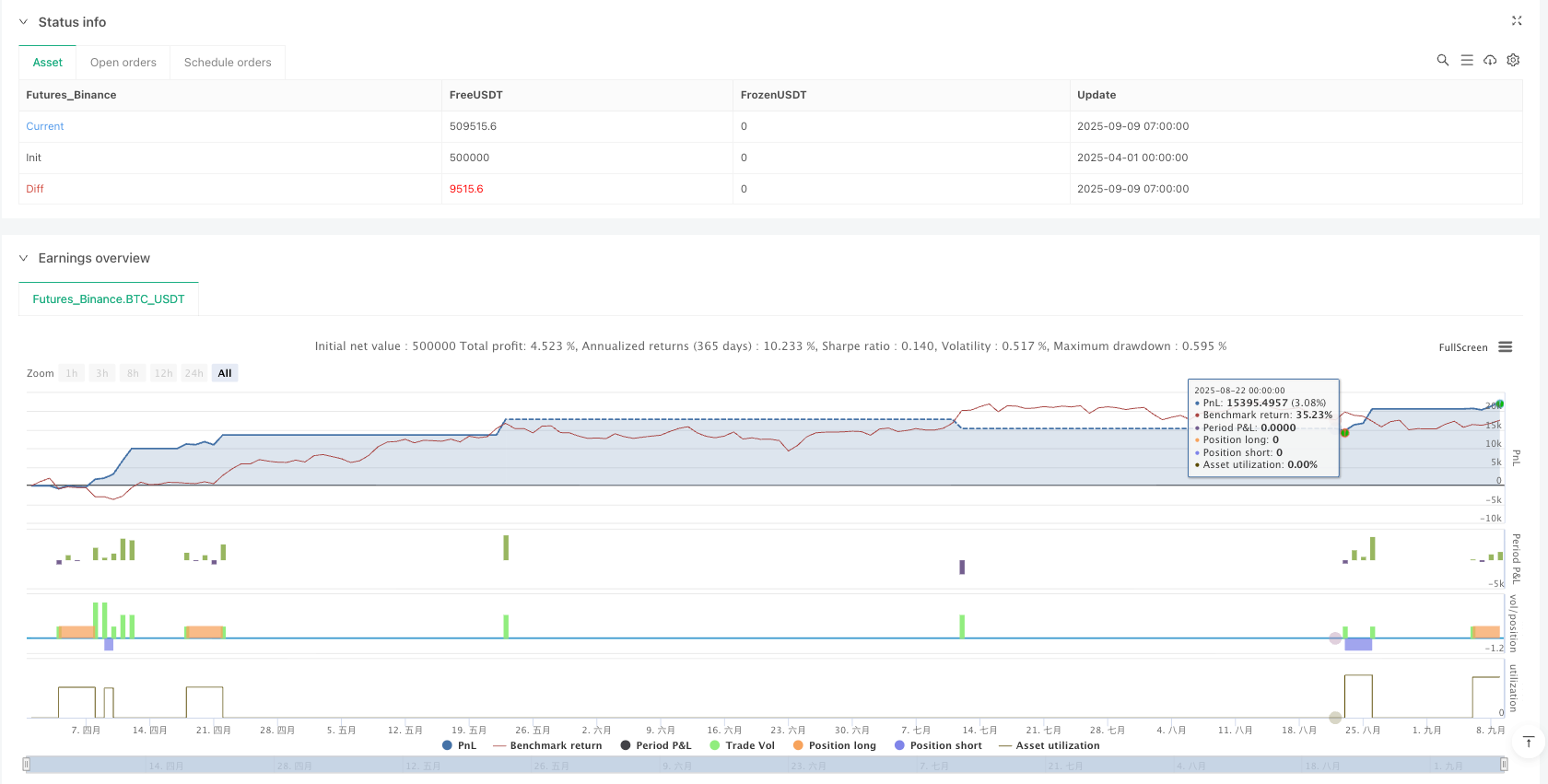
/*backtest
start: 2025-04-01 00:00:00
end: 2025-09-09 08:00:00
period: 1h
basePeriod: 1h
exchanges: [{"eid":"Futures_Binance","currency":"BTC_USDT","balance":500000}]
*/
//@version=5
strategy("AR(2)-GARCH Strategy", overlay=true)
//策略参数设置:配置AR模型、GARCH模型和交易信号的各项参数
lengthReg = input.int(50, "AR估计窗口", minval=50, maxval=200);//AR模型回归窗口长度
//GARCH波动率模型参数:控制条件方差的计算
useGarch = input.bool(true, "启用GARCH波动率");//是否启用GARCH波动率建模
garchAlpha = input.float(0.1, "GARCH Alpha", minval=0.01, maxval=0.3, step=0.01);//GARCH模型alpha参数
garchBeta = input.float(0.85, "GARCH Beta", minval=0.5, maxval=0.95, step=0.01);//GARCH模型beta参数
//交易信号生成参数:控制买卖信号的敏感度
stdevFactor = input.float(2.0, "标准差倍数", minval=1.0, maxval=3.0, step=0.1);//交易波段的标准差倍数
//风险控制参数:设置止损止盈水平
stopLossPerc = input.float(2.0, "止损 (%)", minval=0.5, maxval=5.0, step=0.1);//止损百分比
takeProfitPerc = input.float(4.0, "止盈 (%)", minval=1.0, maxval=10.0, step=0.1);//止盈百分比
//RSI过滤器参数:添加技术指标过滤条件
useRsiFilter = input.bool(false, "启用RSI过滤");//是否启用RSI过滤器
rsiLen = input.int(14, "RSI周期", minval=7, maxval=21);//RSI指标计算周期
rsiOB = input.float(70, "RSI超买线", minval=60, maxval=80);//RSI超买阈值
rsiOS = input.float(30, "RSI超卖线", minval=20, maxval=40);//RSI超卖阈值
//数据预处理:计算收益率序列
rawPrice = close;//原始收盘价
returns = math.log(rawPrice / rawPrice[1]);//对数收益率序列
//获取滞后收益率数据:AR(2)模型需要前两期的收益率数据
returns1 = returns[1];//滞后1期的收益率
returns2 = returns[2];//滞后2期的收益率
//计算收益率序列的移动平均值:作为AR模型的均值项
returnsMean = ta.sma(returns, lengthReg);//收益率的简单移动平均
//AR(2)模型系数计算:使用Yule-Walker方程求解自回归系数
//自协方差函数计算:计算不同滞后期的自协方差
calcAutoCovariance(data, lag, length) =>
mean = ta.sma(data, length);//计算数据的均值
sum = 0.0;//协方差累计值
count = 0;//有效数据点计数
for i = lag to length - 1
if not na(data[i]) and not na(data[i-lag])
sum := sum + (data[i] - mean) * (data[i-lag] - mean);//计算协方差分子
count := count + 1;//累计有效数据点
count > 0 ? sum / count : 0.0;//返回协方差值
//计算AR(2)模型所需的自协方差:用于Yule-Walker方程
c0 = calcAutoCovariance(returns, 0, lengthReg);//滞后0期的自协方差(即方差)
c1 = calcAutoCovariance(returns, 1, lengthReg);//滞后1期的自协方差
c2 = calcAutoCovariance(returns, 2, lengthReg);//滞后2期的自协方差
//Yule-Walker方程求解:计算AR(2)模型的两个自回归系数
// φ₁ = (c₁c₀ - c₂c₁) / (c₀² - c₁²)
// φ₂ = (c₂c₀ - c₁²) / (c₀² - c₁²)
denominator = c0 * c0 - c1 * c1;//分母计算
phi1 = denominator != 0 ? (c1 * c0 - c2 * c1) / denominator : 0.0;//第一个自回归系数
phi2 = denominator != 0 ? (c2 * c0 - c1 * c1) / denominator : 0.0;//第二个自回归系数
//AR(2)稳定性检验:确保模型稳定性条件 |φ₁| + |φ₂| < 1 且 |φ₂| < 1
stabilityCheck = math.abs(phi1) + math.abs(phi2);//计算系数绝对值之和
if stabilityCheck >= 0.99 or math.abs(phi2) >= 0.99
scaleFactor = 0.95 / math.max(stabilityCheck, math.abs(phi2) + 0.01);//计算缩放因子
phi1 := phi1 * scaleFactor;//调整第一个系数
phi2 := phi2 * scaleFactor;//调整第二个系数
//AR(2)收益率预测:根据历史收益率和AR系数预测下一期收益率
arReturnPredict = returnsMean + phi1 * (returns1 - returnsMean) + phi2 * (returns2 - returnsMean);//AR(2)预测公式
//计算AR模型的预测残差:用于GARCH建模
arResidual = returns - arReturnPredict;//AR模型的预测残差
//GARCH(1,1)波动率建模:对AR残差进行条件方差建模
var float garchVariance = na;//GARCH方差变量
var float longTermVar = na;//长期方差变量
//长期方差初始化:使用历史残差计算初始方差值
if na(longTermVar) and bar_index > lengthReg
longTermVar := ta.variance(arResidual, lengthReg);//计算长期方差
//GARCH参数调整:确保参数满足收敛条件
adjustedAlpha = garchAlpha;//调整后的alpha参数
adjustedBeta = garchBeta;//调整后的beta参数
sumParam = garchAlpha + garchBeta;//参数和
if sumParam >= 0.999
scale = 0.99 / sumParam;//计算参数缩放比例
adjustedAlpha := garchAlpha * scale;//调整alpha参数
adjustedBeta := garchBeta * scale;//调整beta参数
//GARCH(1,1)递归更新:根据GARCH公式更新条件方差
if useGarch and not na(longTermVar) and not na(arResidual)
if na(garchVariance)
garchVariance := longTermVar;//初始化GARCH方差
else
omega = (1 - adjustedAlpha - adjustedBeta) * longTermVar;//GARCH常数项
garchVariance := omega + adjustedAlpha * math.pow(arResidual[1], 2) + adjustedBeta * garchVariance[1];//GARCH递归公式
//条件标准差计算:从条件方差计算标准差
garchStd = useGarch and not na(garchVariance) ? math.sqrt(math.max(garchVariance, 0.0001)) : ta.stdev(arResidual, 20);//启用GARCH时使用条件标准差,否则使用历史标准差
//收益率空间的置信区间构建:基于AR预测和GARCH波动率
upperReturnBand = arReturnPredict + stdevFactor * garchStd;//上轨:预测收益率加上标准差倍数
lowerReturnBand = arReturnPredict - stdevFactor * garchStd;//下轨:预测收益率减去标准差倍数
//将置信区间转换为价格空间:用于实际交易信号生成
//基于预测收益率计算预测价格
predictedPrice = rawPrice[1] * math.exp(arReturnPredict);//根据预测收益率计算预测价格
upperPriceBand = rawPrice[1] * math.exp(upperReturnBand);//上轨价格
lowerPriceBand = rawPrice[1] * math.exp(lowerReturnBand);//下轨价格
//交易信号生成:基于当前价格相对于置信区间的位置
longSignal = rawPrice < lowerPriceBand;//做多信号:当前价格低于下轨
shortSignal = rawPrice > upperPriceBand;//做空信号:当前价格高于上轨
//RSI过滤器:使用RSI指标过滤交易信号
if useRsiFilter
rsi = ta.rsi(rawPrice, rsiLen);//计算RSI指标
longSignal := longSignal and rsi < rsiOS;//做多信号需要RSI超卖确认
shortSignal := shortSignal and rsi > rsiOB;//做空信号需要RSI超买确认
//策略执行:根据交易信号开仓和平仓
//开仓操作:根据信号建立多头或空头仓位
if longSignal
strategy.entry("Long", strategy.long);//开多仓
if shortSignal
strategy.entry("Short", strategy.short);//开空仓
//风险控制:设置止损止盈条件
if strategy.position_size > 0
strategy.exit("Long Exit", "Long",
stop=strategy.position_avg_price * (1 - stopLossPerc/100),
limit=strategy.position_avg_price * (1 + takeProfitPerc/100));//多仓止损止盈
if strategy.position_size < 0
strategy.exit("Short Exit", "Short",
stop=strategy.position_avg_price * (1 + stopLossPerc/100),
limit=strategy.position_avg_price * (1 - takeProfitPerc/100));//空仓止损止盈
//图表显示:在图表上绘制价格、预测线和交易信号
//主要价格线和预测线:显示实际价格和基于收益率预测的价格
plot(rawPrice, color=color.white, linewidth=1, title="价格");//绘制实际价格线
plot(predictedPrice, color=color.blue, linewidth=2, title="预测价格");//绘制预测价格线
plot(upperPriceBand, color=color.red, linewidth=1, title="上轨");//绘制上轨线
plot(lowerPriceBand, color=color.green, linewidth=1, title="下轨");//绘制下轨线
//交易信号标记:在图表上标记买卖信号点
plotshape(longSignal, style=shape.triangleup, location=location.belowbar,
color=color.green, size=size.small, title="买入");//标记买入信号
plotshape(shortSignal, style=shape.triangledown, location=location.abovebar,
color=color.red, size=size.small, title="卖出");//标记卖出信号