Les crypto-monnaies sont une nouvelle catégorie d’actifs dont les chercheurs commencent à mieux comprendre les forces fondamentales derrière leur évolution des prix. Un nouveau document de recherche montre que le prix du bitcoin peut être modélisé par la loi de Metcalfe.

Résumé:

Nous démontrons par exemple que le prix à long terme du bitcoin n’est pas aléatoire et peut être modélisé comme une fonction de croissance du nombre d’utilisateurs n au fil du temps. En utilisant les données observées sur Facebook et le bitcoin, nous déduisons la relation entre le prix, le nombre d’utilisateurs et le temps et montrons que la valeur marchande des revenus peut obéir à la fonction de croissance sigmoïde de Gompertz. Cette fonction a été utilisée historiquement pour décrire la croissance d’organismes biologiques tels que les bactéries, les tumeurs et les virus et peut avoir une certaine application dans l’économie du réseau. Nous concluons que le taux de croissance à long terme des utilisateurs a une influence considérable sur le prix à long terme du bitcoin.

Citations remarquables dans des articles de recherche académique:

Cet article fournit une explication simple de la formation des prix dans l’écosystème émergent et souvent mal compris des crypto-monnaies. Avec Bitcoin, par exemple, nous fournissons des preuves empiriques convaincantes que la formation des prix n’est pas le résultat semi-aléatoire d’un investissement émotionnel, mais est basée sur un principe de l’économie de la valeur qui n’a commencé à être reconnu que récemment: l’économie du réseau.

L’examen du prix du bitcoin a fourni des observations intéressantes qui réfutent directement le mythe selon lequel la valeur du bitcoin est une énigme. Tout d’abord, comme les partisans l’ont longtemps soutenu, la valeur d’une monnaie dépend principalement de son utilisation et de son acceptation. Cette hypothèse a été vérifiée et, à un examen approximatif, la relation entre le prix du bitcoin et les activités liées au réseau de paiement bitcoin est également évidente.

La loi de Metcalfe est basée sur une grammaire mathématique qui décrit les connexions entre n utilisateurs. Par conséquent, la valeur du réseau V est une fonction du nombre d’utilisateurs n. La base mathématique de la loi de Metcalfe est basée sur les connexions en paires (par exemple, le téléphone).

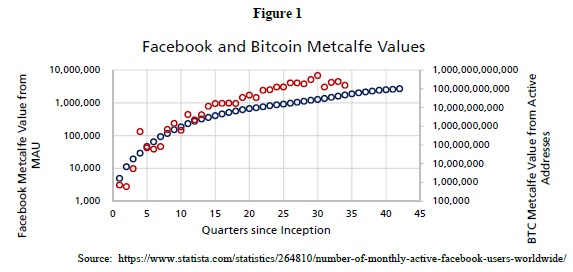
Facebook est très bien comparé à Bitcoin. Chaque série de données a une longueur presque identique (environ 10 ans). Les deux sont assez innovants, bien que pas entièrement originaux (Digicash avant Bitcoin, MySpace avant Facebook). Il est rare de voir une monnaie ou un autre actif être adopté progressivement au fil du temps.

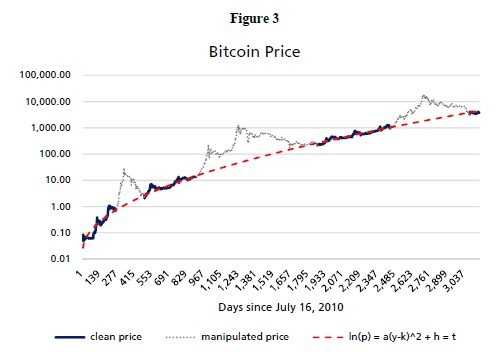
En regardant le graphique 3, il y a trois exceptions notables, la tendance du prix de Bitcoin à s’écarter de la parallèle. Ce sont des périodes de manipulation des prix enregistrées et d’équilibre final. Ces pics représentent des écarts de prix qui ne peuvent pas être expliqués par des facteurs liés à l’utilisateur.

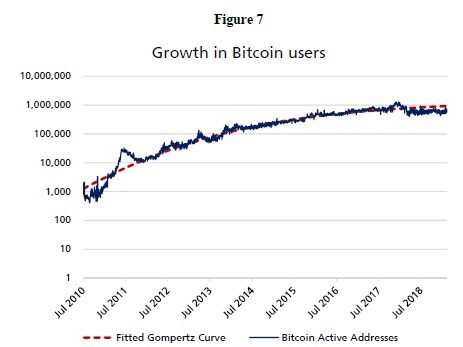
Si n croît à un taux constant, alors log (n) est linéaire. Comme nous l’avons observé dans Facebook et Bitcoin (figure 7), log (n) est non linéaire, donc n croît à un taux non constant, indiquant que l’adoption est à des stades différents. Ce modèle de taux de croissance cumulatif a donné naissance à la fonction en forme de S (la fonction Gompertz) qui a été utilisée pendant des décennies pour simuler les infections virales, la croissance bactérienne, la croissance tumorale et la popularité des téléphones portables.[2018], il l’utilise pour simuler le coefficient de parenté de Metcalfe. En utilisant les données quotidiennes de n comptes actifs d’agents, nous avons adapté cette équation à l’adresse active de la figure 7.

Il est également connu pour être le créateur du premier bitcoin, le Bitcoin Code, qui a été publié en décembre de l’année dernière.