Pouvez-vous distancer les gorilles en pariant (en échangeant) avec des machines vectorielles SVM ?

Mesdames et messieurs, faites vos mises. Aujourd’hui, nous allons faire de notre mieux pour vaincre un orang-outan, considéré comme l’un des plus redoutables adversaires du monde financier. Nous allons essayer de prédire le rendement d’une variété de crypto-monnaie le lendemain. Je vous assure que même battre un singe au hasard avec une chance de victoire de 50% est une tâche difficile. Nous utiliserons un algorithme d’apprentissage automatique prêt à l’emploi qui prend en charge les classificateurs vectoriels. Les machines vectorielles SVM sont une méthode incroyablement puissante pour résoudre des tâches de régression et de classification.

• Vecteur supporté par SVM

La machine vectorielle SVM est basée sur l’idée que l’on peut classer l’espace caractéristique par p-pièces en utilisant un superplan. L’algorithme de la machine vectorielle SVM utilise un superplan et une marge de reconnaissance pour créer une frontière de décision de classification, comme illustré ci-dessous.

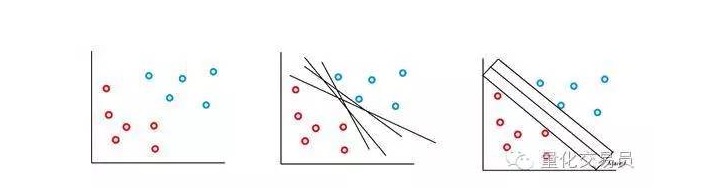
Dans le cas le plus simple, un classement linéaire est possible. L’algorithme choisit une frontière de décision qui maximise la distance entre les classes.

Dans la plupart des séquences de temps financiers auxquelles vous êtes confronté, il est peu probable que vous rencontriez des ensembles simples et linéairement séparables, mais les situations où ils ne sont pas séparables sont fréquentes. Le vecteur SVM a résolu ce problème en mettant en œuvre une méthode appelée méthode de la marge douce.

Dans ce cas, certains cas de classification erronée sont autorisés, mais ils exécutent eux-mêmes la fonction pour réduire au minimum le facteur et la distance de l’erreur à la frontière de manière à être proportionnelle à C (des erreurs de coût ou de budget peuvent être autorisées).

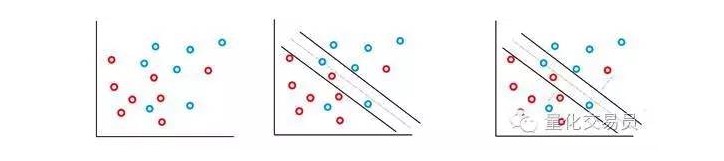
Fondamentalement, la machine va maximiser l’espacement entre les classifications tout en minimisant les pénalités sur lesquelles elle est pondérée par C.

Le classificateur SVM possède une caractéristique intéressante: la position et la taille des frontières de décision de classification ne sont déterminées que par une partie des données, c’est-à-dire la partie la plus proche de la frontière de décision. Cette caractéristique de l’algorithme lui permet de résister à l’interférence des valeurs anormales de longue distance.

C’est trop compliqué ? Eh bien, je pense que le plaisir ne fait que commencer.

Considérez les situations suivantes (séparer les points rouges des autres couleurs):

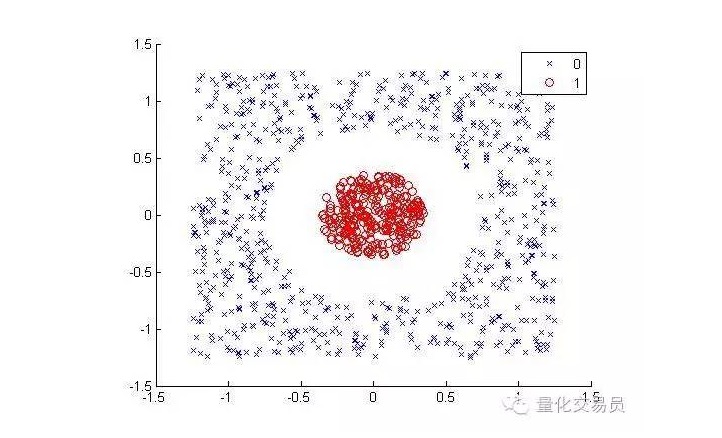
Pour les humains, c’est assez simple à classer (un ellipse, c’est bien) mais pour les machines c’est différent. Il est évident qu’il ne peut pas être fait en ligne droite (une ligne droite ne peut pas séparer les points rouges). Ici, nous pouvons essayer la ruse du noyau de l’acier (truc du noyau).

La technique du noyau interne est une technique mathématique très intelligente qui nous permet de résoudre des problèmes de classification linéaire dans un espace de dimension supérieure. Voyons maintenant comment cela est fait.

Nous allons transformer l’espace caractéristique en deux dimensions en trois dimensions par une cartographie en ascension, et retourner à la deuxième dimension une fois la classification terminée.

Ci-dessous, une carte en hauteur et une classification complète:

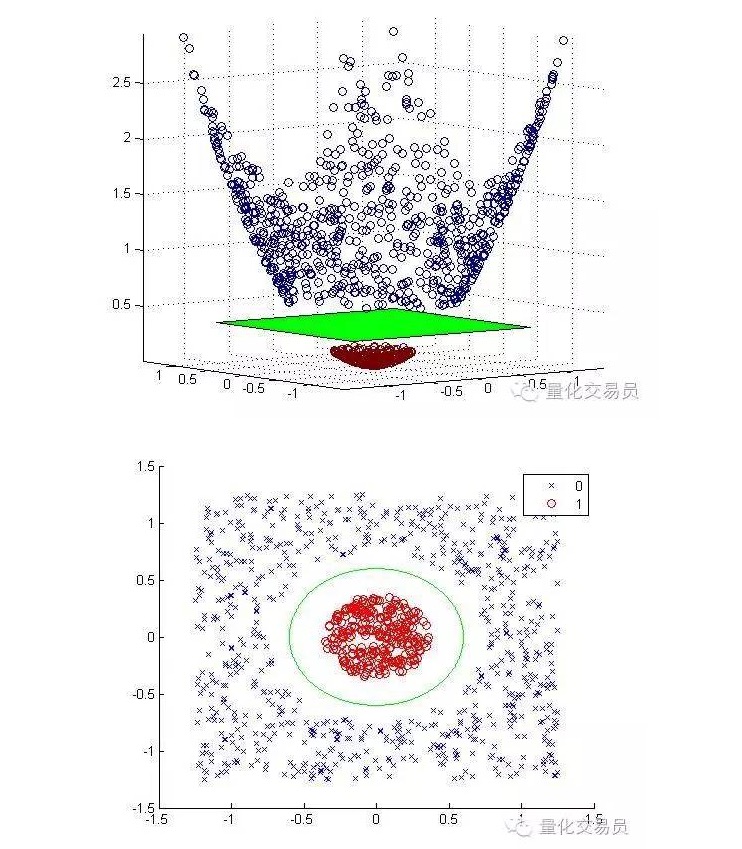
Généralement, si vous avez d’entrées, vous pouvez utiliser un mappage de l’espace d’entrée en d dimensions vers l’espace de caractéristiques en p dimensions. Exécutez la solution que produira l’algorithme de minimisation ci-dessus, puis mappez-la vers le superplan de p dimensions de votre espace d’entrée original.

La prémisse importante de la solution mathématique ci-dessus dépend de la façon dont on génère de bons ensembles d’échantillons de points dans l’espace caractéristique.

Vous n’avez besoin que de ces ensembles de points pour effectuer l’optimisation des limites, la cartographie n’a pas besoin d’être explicite, et les points d’espace d’entrée dans l’espace de caractéristiques en haute dimension peuvent être calculés en toute sécurité par la fonction noyau (avec l’aide de la fonction de Mercer et un peu du théorème de Mercer).

Par exemple, si vous voulez résoudre votre problème de classification dans un espace de caractéristiques énorme, disons 100000 dimensions. Pouvez-vous imaginer la puissance de calcul dont vous auriez besoin ? Je doute fortement que vous puissiez le faire.

• Le défi et le gorille

Maintenant, nous sommes prêts à affronter le défi de vaincre la capacité de prédiction de Jeff.

Jeff est un expert des marchés monétaires qui, grâce à des paris aléatoires, est capable d’obtenir une précision de prévision de 50%, une précision qui est le signal de la prévision des rendements du jour de négociation suivant.

Nous utiliserons différentes séquences temporelles de base, y compris des séquences temporelles de prix en temps réel, avec des gains de jusqu’à 10 lags par séquence, pour un total de 55 fonctionnalités.

Le vecteur SVM que nous sommes sur le point de construire utilise un noyau de 3 degrés. Vous pouvez imaginer que choisir un noyau approprié est une autre tâche très difficile, car pour calibrer les paramètres C et Γ, la triple vérification de croix fonctionne sur une grille de combinaisons de paramètres possibles, et le meilleur ensemble sera sélectionné.

Les résultats ne sont pas très encourageants:

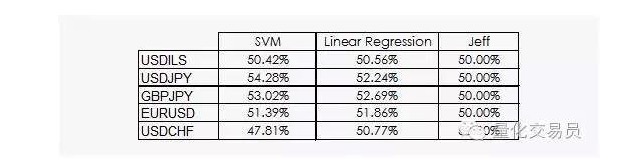
Nous pouvons voir que la régression linéaire et la machine à vecteurs SVM peuvent battre Jeff. Bien que les résultats ne soient pas optimistes, nous pouvons également extraire des informations des données, ce qui est déjà une bonne nouvelle, car dans la discipline des données, les gains quotidiens des séquences de temps financières ne sont pas les plus utiles.

Après la vérification croisée, les ensembles de données seront entraînés et testés, et nous enregistrerons les capacités de prévision de la SVM entraînée. Afin d’avoir une performance stable, nous répéterons la division aléatoire de chaque devise 1000 fois.

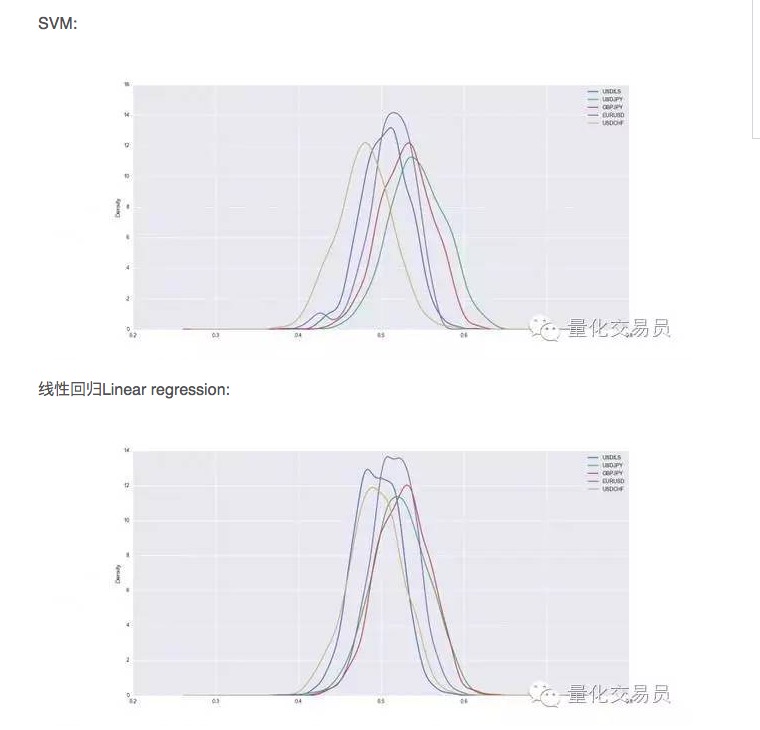
Ainsi, il semble que la SVM soit supérieure à la simple régression linéaire dans certains cas, mais la différence de performance est légèrement plus grande. Dans le cas du dollar contre le yen, par exemple, nous prévoyons en moyenne 54% du nombre total de signaux. C’est un bon résultat, mais regardons de plus près !

Ted est le cousin de Jeff, qui est aussi un gorille, bien sûr, mais il est plus intelligent que Jeff. Ted se concentre sur l’ensemble des échantillons de formation plutôt que sur les paris aléatoires.

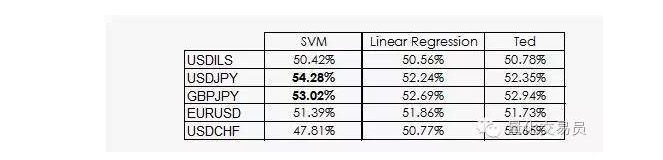
Comme nous l’avons vu, la performance de la plupart des SVM vient simplement du fait que la machine apprend que la classification est peu susceptible d’être équivalente à l’a priori. En fait, la régression linéaire ne peut pas obtenir d’informations de l’espace des traits, mais l’intersection ((intercept) est significative dans la régression, et le fait que l’intersection et l’intersection d’une classification fonctionnent mieux est lié à cela.

Une bonne nouvelle, c’est que le vecteur SVM est capable d’obtenir des informations non linéaires supplémentaires à partir des données, ce qui nous permet d’avoir une précision de prédiction d’environ 2%.

Malheureusement, nous ne savons pas encore ce que cela pourrait être, tout comme les vecteurs SVM ont leurs propres inconvénients majeurs, que nous ne pouvons pas expliquer clairement.

Auteur: P. López, publié dans quantdare Il a été publié dans la revue WeChat Public.