Formule de Kelly – un outil puissant pour le contrôle de position

Si vous gagnez, vous gagnez un dollar pour chaque dollar que vous déposez, et si vous perdez, vous perdez un dollar pour chaque dollar que vous déposez. Le pari peut être effectué un nombre illimité de fois, et chaque fois, vous pouvez choisir votre mise. Question: Si votre capital initial est de 100 dollars, comment parier, c’est-à-dire quel pourcentage de votre capital à chaque fois, pour maximiser les gains à long terme?

• 1, pour ce pari, le gain attendu sur chaque mise est de 60% du montant mis.*1-40%*1 = 20%, le rendement attendu est positif. C’est-à-dire qu’il s’agit d’une impasse où les pirates ont le dessus, et ils ont un avantage énorme.

Alors, comment parier ?

Si nous ne réfléchissons pas sérieusement, et si nous imaginons à la légère, nous pourrions penser que puisque je m’attends à un rendement de 20% sur chaque pari, pour obtenir le plus grand rendement à long terme, je devrais essayer de placer un plus grand pourcentage de capital dans chaque pari.

Mais il est évident qu’il n’est pas raisonnable d’investir 100% de son capital dans chaque partie de jeu, car une fois que le joueur a perdu, il perdra tout son capital, ne pourra plus participer au prochain tour et ne pourra quitter le jeu.

Donc, la conclusion est que si une position est bloquée, la possibilité de perdre tout le capital, même si cette possibilité est très faible, ne peut jamais être remplie. Parce qu’à long terme, les événements à faible probabilité sont inévitables, et que dans la vie réelle, la probabilité réelle d’un événement à faible probabilité est beaucoup plus grande que sa probabilité théorique. C’est l’effet de queue de graisse en finance.

• 2/ Retour à l’impasse 1. Si le pari à 100% est déraisonnable à chaque fois, que dire de 99% ? Si le pari à 99% est déraisonnable à chaque fois, non seulement on est assuré de ne jamais être en faillite, mais on peut aussi, avec de la chance, réaliser d’énormes gains.

Est-ce que c’est vraiment comme ça ?

On ne va pas analyser le problème théoriquement, on va faire une expérience. On va simuler la impasse, et on va miser 99% à chaque fois pour voir ce qui se passera.

Cette simulation est très simple et peut être réalisée en utilisant Excel.

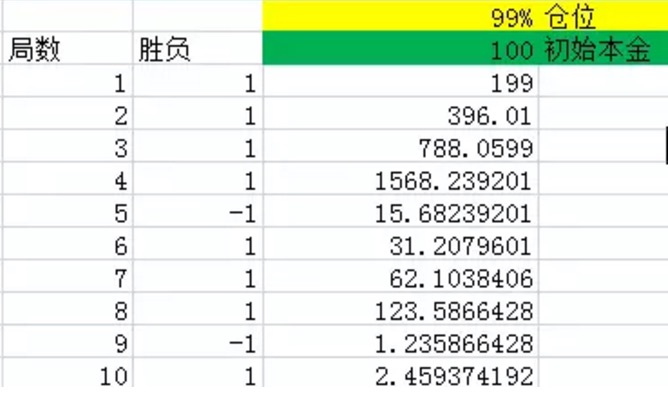Figure 1

La première colonne représente le nombre de tours. La deuxième colonne représente le nombre de tours gagnés. Excel génère un 1 avec une probabilité de 60%, soit un rendement net de 60% avec une probabilité de 1,40% avec un rendement net de 40%, soit un rendement net de -1. La troisième colonne représente tous les fonds du jeu à la fin de chaque tour.

Comme vous pouvez le voir sur le graphique, après 10 tours, le nombre de tours gagnés en 10 tours est de 8, soit une probabilité plus grande que 60%, avec seulement deux défaites. Mais même ainsi, le dernier argent ne reste que 2,46 yuans, ce qui est essentiellement une perte de lumière.

Quand j’augmente le nombre d’expériences à 1000, 2000, 3000… vous pouvez imaginer que la somme des fonds en main est essentiellement orientée vers 0.

Mais comme 99% ne fonctionne pas, nous allons essayer avec quelques autres proportions, comme le montre le graphique suivant: Comme on peut le voir sur le graphique, lorsque la position est réduite progressivement, de 99%, à 90%, 80%, 70%, 60%, le résultat des mêmes 10 tours est complètement différent. On peut voir sur le graphique que les fonds après 10 tours deviennent de plus en plus importants à mesure que la position diminue progressivement.

Si vous regardez ici, vous vous rendrez compte que la question de l’impasse n’est pas aussi simple que cela. Même si les pirates dominent une impasse aussi grande, ils ne peuvent pas gagner de l’argent à la légère.

Alors, comment parier pour maximiser les gains à long terme ?

Est-ce que c’est mieux de réduire le ratio, comme le montre la figure ci-dessus ? Non, car il est évident qu’il n’y a pas d’argent à gagner quand le ratio est réduit à zéro.

Alors, quel est ce ratio optimal ?

C’est le problème que la célèbre formule de Kelly doit résoudre !

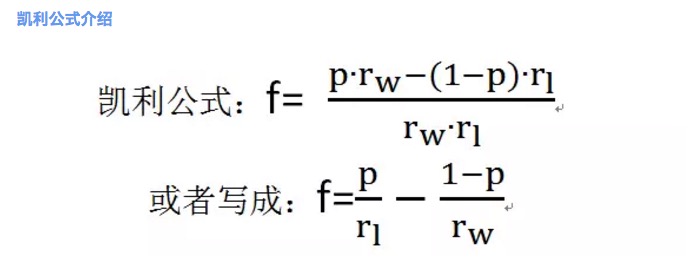Voir le graphique 2.

où f est le pourcentage de mise optimal; p est la probabilité de gagner; rw est le taux de gain net en cas de victoire, par exemple, dans le cas où rw est égal à 1; rl est le taux de perte net en cas de perte, par exemple, dans le cas où rl est égal à 1; notez que rl > 0;

Selon la formule de Kelly, on peut calculer que le pourcentage le plus élevé de mise dans un tirage au sort 1 est de 20%.

Nous pouvons faire des expériences pour mieux comprendre cette conclusion.

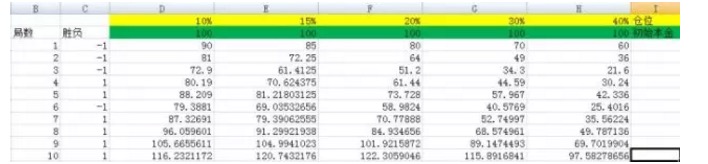Voir aussi la figure 3.

Dans la figure ci-dessous, nous définissons les positions comme étant respectivement 10%, 15%, 20%, 30% et 40%. Le nombre de colonnes correspondant est D, E, F, G et H.

Et quand j’ai fait les expériences à 3000 fois, il y avait une différence. Et quand j’ai fait le test 5 000 fois, j’ai trouvé que c’était un peu plus de la même chose. Vous pouvez voir que la colonne F correspond à la plus grande des conséquences, et que la racine de compression par rapport aux autres colonnes n’est pas un ordre de grandeur.

Vous voyez la puissance de la formule de Kelly. Dans l’expérience ci-dessus, si vous avez eu le malheur de choisir un ratio de 40%, c’est-à-dire la colonne H correspondante, alors après 5000 jeux, votre capital est passé de 100 à 22799985.75, ce qui représente un gain considérable. Mais par rapport au résultat du ratio de 20%, c’est vraiment l’équivalent de ne pas gagner de l’argent.

C’est le pouvoir de la connaissance !

• 3 Comprendre la formule de Kelly

La déduction mathématique de l’équation de Kelly et sa complexité nécessitent une connaissance mathématique très approfondie, il n’y a donc pas de sens à en discuter ici. Ici, je vais approfondir la compréhension subjective de l’équation de Kelly à travers quelques expériences.

Nous allons voir un autre pari. Pari 2: la probabilité que vous perdiez et gagniez est de 50% respectivement. Par exemple, lancer une pièce.

Il est facile de voir que le gain attendu pour la paralysie 2 est de 0.25, une paralysie dans laquelle les joueurs ont un avantage considérable.

Selon la formule de Kelly, on obtient un ratio optimal de mise par partie de:

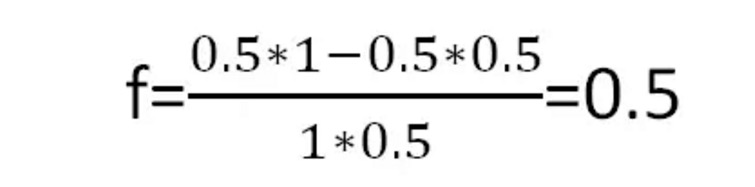Voir aussi la figure 4.

C’est-à-dire que chaque fois que vous prenez la moitié de votre argent pour parier, vous obtenez le plus de bénéfices à long terme.

Je vais maintenant essayer de trouver une notion de taux de croissance moyen r, basée sur des expériences.

Pour commencer, jetons un coup d’œil à l’expérience 2.1:

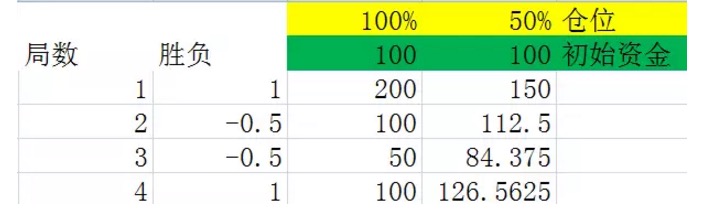Voir le graphique 5.

Les deux graphiques sont des expériences de simulation d’une impasse 2, avec une probabilité de 50% de succès dans la deuxième colonne, 1, représentant un gain de 100%; une probabilité de 50% de succès, -0.5; une perte de 50%; et une troisième et quatrième colonne représentant les fonds détenus après chaque impasse avec des positions de 100% et 50% respectivement.

En comparant attentivement les deux graphiques, on peut en déduire que, après le même nombre d’étapes, le résultat final est lié uniquement au nombre d’étapes gagnées et au nombre d’étapes perdues dans ces graphiques, et non à l’ordre dans lequel elles ont été gagnées et perdues. Par exemple, dans les deux graphiques précédents, 4 tours ont également été effectués, et deux tours ont également été perdus dans chaque graphique, mais l’ordre de perte du premier graphique est gagnant-gagnant-perdant-gagnant, et l’ordre de perte du deuxième graphique est gagnant-perdant-gagnant-perdant-gagnant.

Bien sûr, cette conclusion est très facile à prouver (la loi de l’échange de multiplication, les élèves du primaire le savent), mais ce n’est pas une preuve, les deux exemples ci-dessus suffisent pour que vous compreniez bien.

Puisque le résultat final n’a rien à voir avec l’ordre des victoires et des défaites, nous supposons que l’arrêt de jeu 2 se déroule comme dans l’expérience 2.2.

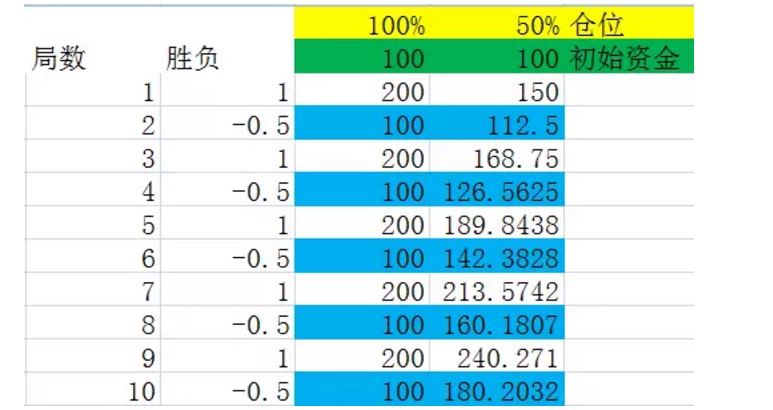Voir aussi la figure 6.

Nous supposons que la victoire ou la défaite d’un tirage au sort se produisent en alternance, ce qui n’a aucune incidence sur le résultat financier à long terme, étant donné la conclusion 1.

Avant d’examiner le tableau, nous définissons un ensemble que nous appelons un ensemble de barrages. En supposant que nous considérions un ensemble de barrages comme un ensemble dans lequel la fréquence des résultats est exactement égale à sa probabilité, et dont le nombre de barrages est le plus petit nombre moyen parmi tous les ensembles de barrages qui satisfont aux conditions, nous appelons cet ensemble un ensemble de barrages. Par exemple, dans l’expérience de la figure ci-dessus, un ensemble de barrages représente deux barrages, dont l’un est gagné et l’autre perdu.

Observez attentivement les chiffres marqués en bleu dans le graphique ci-dessus, ils sont à la fin d’une série de barrages. Vous trouverez que ces chiffres ont une croissance stable. Lorsque la position est de 100%, le taux de croissance des chiffres marqués en bleu est de 0%, c’est-à-dire que le taux de croissance du capital après une série de barrages est de 0%. Cela explique également que chaque fois que les positions sont pleines, il est impossible de gagner de l’argent à long terme dans la série 2.

Il s’agit d’une règle générale selon laquelle le taux de croissance après chaque blocage est lié à la position. Plus le taux de croissance est élevé après chaque blocage, plus le bénéfice final est élevé à long terme.

On peut calculer le taux de croissance moyen de chaque blocage en fonction du taux de croissance de chaque blocage g. Dans le graphique ci-dessus, si chaque blocage contient deux blocs, alors le taux de croissance moyen de chaque blocage

Voir le graphique 7.

Dans le long terme, pour que le capital augmente au maximum, il suffit de maximiser r, c’est-à-dire de maximiser g. Le meilleur ratio de mise f est en fait obtenu en résolvant max (g).

• 4 Autres conclusions de la formule de Kelly sur le risque

La légende de Kelly

La formule de Kelly a été créée à l’origine pour John Larry Kelly, un physicien d’AT&T Bell Labs, sur la base des recherches de son collègue Claude Elwood Shannon sur les messages sur les lignes téléphoniques longues. Kelly a résolu le problème de la façon dont la théorie de l’information de Shannon peut être appliquée à un joueur possédant des informations internes au moment du pari. Il utilise ses connaissances pour attaquer tous les casinos de Reno, au Nevada, en une nuit. Il a réussi à gagner des dizaines de milliers de dollars sur les tables de poker à 21 points. Il est également l’ancêtre du fonds de couverture de trading quantifié de Wall Street aux États-Unis, créant le premier fonds de couverture de trading quantifié dans les années 1970.

Utilisation de la perspective

Comment utiliser la formule de Kelly pour gagner de l’argent dans la vraie vie ? C’est de créer une impasse qui réponde aux conditions de l’application de la formule de Kelly. J’ai fait des recherches sur les systèmes de trading ces derniers temps. Qu’est-ce qui est le plus important pour un bon système de trading ? Une règle d’achat et de vente qui s’attend à des rendements positifs représente 10% de l’importance, tandis qu’une bonne méthode de contrôle des fonds représente 40% de l’importance, et le reste de 50% est le contrôle psychologique de la personne. La formule de Kelly est un outil qui m’aide à contrôler ma position financière. Par exemple, un système de négociation d’actions que j’ai étudié auparavant, qui effectue une transaction par semaine, la probabilité de succès est de 0,8 et la probabilité d’échec est de 0,2 . Lorsque vous réussissez, vous pouvez gagner 3% (déduction de la commission et de l’impôt sur les titres), et chaque fois que vous échouez, vous perdez 5%. Avant de connaître la formule de Kelly, j’étais aveuglément boursier, et je ne savais pas que ma position était incorrecte. Bien sûr, la formule de Kelly ne peut pas être aussi simple dans une application pratique, et il y a beaucoup de difficultés à surmonter. Par exemple, le coût des fonds requis par les bourses à effet de levier, par exemple, le capital n’est pas infiniment divisible dans la réalité, par exemple, dans les marchés financiers, il n’est pas aussi simple que la simple impasse mentionnée ci-dessus. Mais quoi qu’il en soit, la formule de Kelly nous indique la voie à suivre.