Sept techniques de régression à maîtriser

**Cet article explique l’analyse de la régression et ses avantages. Il résume les sept techniques de régression les plus couramment utilisées et leurs éléments clés, tels que la régression linéaire, la régression logique, la régression polynomielle, la régression progressive, la régression en chaîne, la régression en chaîne, la régression ElasticNet, et les éléments clés pour choisir le bon modèle de régression. ** ** L’analyse de la régression par bouton d’éditeur est un outil important pour la modélisation et l’analyse des données. Cet article explique le contenu de l’analyse de la régression et ses avantages. Il résume les sept techniques de régression les plus couramment utilisées, telles que la régression linéaire, la régression logique, la régression polynomial, la régression progressive, la régression en coulisses, la régression en chaîne, la régression ElasticNet, et ses éléments clés.**

• ### Qu’est-ce que la régression ?

L’analyse de la régression est une technique de modélisation prédictive qui étudie les relations entre la variable de cause (objectif) et la variable de résultat (préviseur). Cette technique est généralement utilisée pour l’analyse prédictive, les modèles de séquence temporelle et les relations de causalité entre les variables découvertes. Par exemple, la relation entre la conduite imprudente des conducteurs et le nombre d’accidents de la route est mieux étudiée en régression.

L’analyse de la régression est un outil important pour modéliser et analyser des données. Ici, nous utilisons des courbes/lignes pour adapter ces points de données, de cette façon, la différence de distance entre la courbe ou la ligne et les points de données est minime. Je vais expliquer cela plus en détail dans la section suivante.

• ### Pourquoi utiliser l’analyse de régression ?

Comme indiqué plus haut, la régression permet d’estimer la relation entre deux ou plusieurs variables. Voici un exemple simple pour le comprendre:

Par exemple, dans les conditions économiques actuelles, si vous voulez estimer la croissance des ventes d’une entreprise. Maintenant, vous avez les dernières données de l’entreprise, qui montrent que la croissance des ventes est environ 2,5 fois la croissance économique.

Les avantages de l’analyse de la régression sont multiples:

Il montre une relation significative entre la variable propre et la variable causée.

Elle indique l’intensité de l’influence de plusieurs variables d’origine sur une variable de cause.

L’analyse de la régression nous permet également de comparer les effets réciproques entre les variables qui mesurent les différentes échelles, telles que les liens entre les variations de prix et le nombre d’activités promotionnelles. Cela est utile pour aider les chercheurs de marché, les analystes de données et les scientifiques de données à exclure et à estimer le meilleur ensemble de variables pour construire des modèles prédictifs.

• ### Combien de techniques de régression avons-nous ?

Il existe une grande variété de techniques de régression utilisées pour la prévision. Ces techniques sont principalement décrites en trois dimensions: le nombre d’individus de la variable, le type de variable et la forme de la ligne de régression. Nous en discuterons plus en détail dans la section suivante.

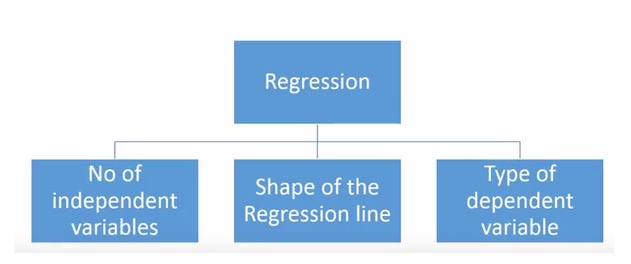
Pour ceux qui sont créatifs, vous pouvez même créer un modèle de régression qui n’a pas été utilisé si vous trouvez nécessaire d’utiliser une combinaison des paramètres ci-dessus. Mais avant de commencer, découvrez les méthodes de régression les plus couramment utilisées:

• 1. régression linéaire

  C’est l’une des techniques de modélisation les plus connues. La régression linéaire est généralement l’une des techniques de prédilection pour apprendre des modèles prédictifs.

  La régression linéaire utilise une ligne droite de conjonction optimale (c’est-à-dire la ligne de régression) pour établir une relation entre la variable de cause (y) et une ou plusieurs variables d’effet (x).

  On peut l’exprimer avec une équation, Y = a + b.*X + e, où a représente l’intersection, b représente la pente de la ligne droite, et e est l’erreur. Cette équation permet de prédire la valeur de la variable cible en fonction de la variable de prévision donnée (s).

  

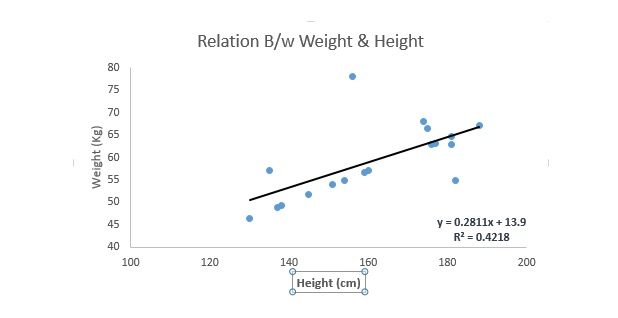
  La différence entre la régression monolinéaire et la régression multilinéaire est que la régression multilinéaire a (< 1) une variable propre, alors que la régression monolinéaire n’a généralement qu’une seule variable propre. La question est maintenant de savoir comment obtenir une ligne d’adéquation optimale.

  Comment obtenir la valeur de la ligne de la meilleure adéquation (a et b)?

  Le problème peut être facilement résolu en utilisant la méthode de la multiplication par deux minimale. La multiplication par deux minimale est également la méthode la plus couramment utilisée pour la conjugaison des lignes de régression. Pour les données d’observation, elle permet de calculer la ligne de conjugaison optimale en minimisant la somme des squares de la déviation verticale de chaque point de données vers la ligne.

  

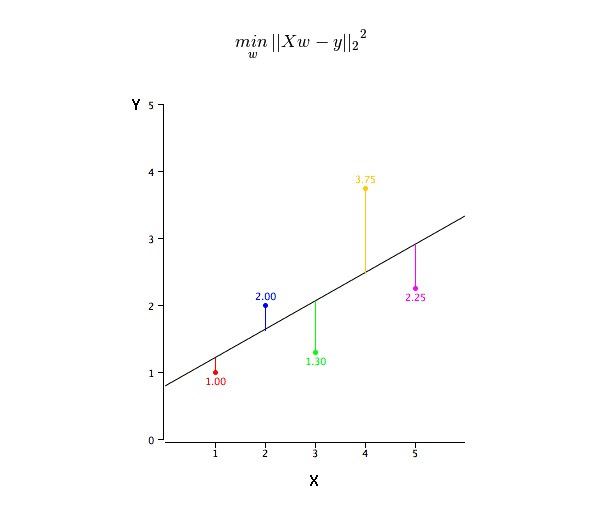
  Nous pouvons utiliser les R-square pour évaluer la performance du modèle. Pour plus de détails sur ces indicateurs, voir: Indicateurs de performance du modèle Part 1, Part 2 .

  Le point:

  • Il doit y avoir une relation linéaire entre la variable auto et la variable cause.
  • La régression plurielle présente une co-linéarité, une auto-corrélation et une divergence multiples.
  • La régression linéaire est très sensible aux anomalies. Elle affecte gravement la ligne de régression et, finalement, les valeurs de prévision.
  • La co-linéarité multiple augmente la variance de l’estimation des coefficients, ce qui rend l’estimation extrêmement sensible à de légères variations du modèle. Le résultat est une estimation instable des coefficients.
  • Dans le cas de plusieurs variables autonomes, nous pouvons choisir la variable autonome la plus importante en utilisant la sélection avant, la suppression arrière et le filtrage par étapes.

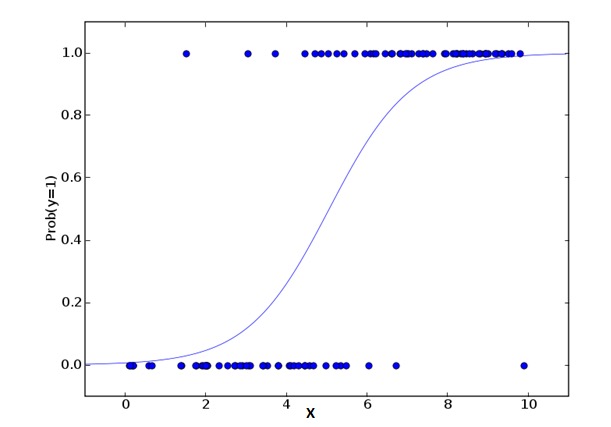
• 2.Régression logistique

  La régression logique est utilisée pour calculer la probabilité que Success=Success et Failure=Failure se produisent. On devrait utiliser la régression logique lorsque le type de la variable est une variable binaire ({¹⁄₀, true/false, yes/no}). Ici, la valeur de Y est de 0 à 1, elle peut être représentée par l’équation suivante:

  odds= p/ (1-p) = probability of event occurrence / probability of not event occurrence
  ln(odds) = ln(p/(1-p))
  logit(p) = ln(p/(1-p)) = b0+b1X1+b2X2+b3X3....+bkXk
  

  Dans la formule ci-dessus, p représente la probabilité d’avoir une certaine caractéristique. Vous devriez vous poser la question suivante: pourquoi utiliser le logarithme dans l’équation ?

  Puisque nous utilisons ici la distribution binaire (en fonction des variables), nous devons choisir une fonction de liaison optimale pour cette distribution. C’est la fonction Logit. Dans l’équation ci-dessus, les paramètres sont choisis en observant les valeurs de probabilité maximale de l’échantillon, plutôt que de minimiser le carré et l’erreur (comme dans la régression ordinaire).

  

  Le point:

  • Il est largement utilisé pour les questions de classification.
  • La régression logique n’exige pas que les variables elles-mêmes et les variables de cause soient des relations linéaires. Elle peut traiter différents types de relations, car elle utilise une conversion logarithmique non linéaire sur l’indice de risque relatif OR prévu.
  • Afin d’éviter les surcorrélations et les surcorrélations, nous devrions inclure toutes les variables importantes. Il existe une bonne façon de s’assurer que cela se produit en utilisant une méthode de filtrage progressif pour estimer la régression logique.
  • Il nécessite un grand nombre d’échantillons, car dans de plus petits nombres d’échantillons, les effets estimés avec une grande probabilité sont inférieurs à ceux de l’échantillonnage ordinaire par le plus petit carré.
  • Les variables elles-mêmes ne devraient pas être associées entre elles, c’est-à-dire qu’elles ne sont pas multicollineuses. Cependant, dans l’analyse et la modélisation, nous pouvons choisir d’inclure les effets de l’interaction des variables classées.
  • Si la valeur d’une variable par conséquence est une variable de séquence, elle est appelée régression logique séquentielle.
  • Si la variable par conséquence est multiclasse, on parle de régression logique plurielle.

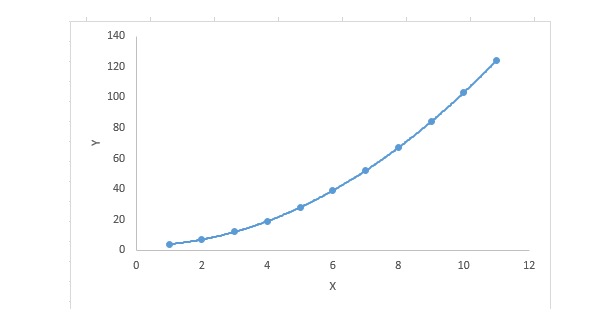
• 3. Régression polynomial

  Pour une équation de régression, si l’indice de la variable est supérieur à 1, alors elle est une équation de régression polynomielle. L’équation suivante:

  y=a+b*x^2
  

  Dans cette technique de régression, la meilleure correspondance n’est pas une ligne droite, mais une courbe utilisée pour correspondre les points de données.

  

  Les points forts:

  • Bien qu’il y ait une induction permettant d’appliquer un polynôme de haut niveau et d’obtenir une erreur inférieure, cela peut entraîner une surapplication. Vous devez régulièrement tracer un diagramme de relation pour voir si la correspondance est correcte et vous concentrer sur la garantie d’une correspondance raisonnable, sans surapplication ni déficience. Voici un diagramme qui peut aider à comprendre:

  

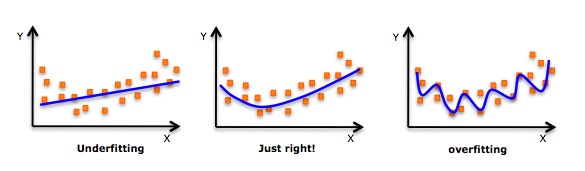
  • Il est évident de chercher des points de la courbe aux deux extrémités pour voir si ces formes et tendances sont significatives. Des polynômes de degré plus élevé peuvent aboutir à des conclusions bizarres.

• 4. Régression par étapes

  On peut utiliser cette forme de régression lorsqu’on traite plusieurs variables autonomes. Dans cette technique, la sélection des variables autonomes est effectuée dans un processus automatisé, qui comprend des opérations non-humaines.

  Cette prouesse consiste à identifier les variables importantes en observant des valeurs statistiques telles que R-square, t-stats et l’indicateur AIC. La régression progressive s’adapte au modèle en ajoutant/supprimant simultanément des co-variables basées sur des critères spécifiés. Voici quelques-unes des méthodes de régression progressive les plus couramment utilisées:

  • La méthode de régression progressive standard fait deux choses: elle ajoute et supprime les prédictions nécessaires à chaque étape.
  • La méthode de sélection avancée commence par les prédictions les plus importantes du modèle, puis ajoute des variables à chaque étape.
  • La méthode d’élimination de l’arrière-plan commence en même temps que toutes les prédictions du modèle, puis élimine les variables les moins significatives à chaque étape.
  • Cette technique de modélisation vise à maximiser la capacité de prévision en utilisant le moins de variables de prévision possible. C’est aussi une des méthodes utilisées pour traiter des ensembles de données à haute dimension.

• 5. Régression de la crête

  L’analyse de la régression alkyle est une technique utilisée pour des données où il existe une grande correspondance entre les variables. Dans le cas de la régression alkyle, les valeurs observées sont si différentes que les valeurs observées sont décalées et éloignées de la valeur réelle.

  Nous avons vu plus haut l’équation de régression linéaire. Vous vous souvenez ?

  y=a+ b*x
  

  L’équation complète est:

  y=a+b*x+e (error term),  [error term is the value needed to correct for a prediction error between the observed and predicted value]
  => y=a+y= a+ b1x1+ b2x2+....+e, for multiple independent variables.
  

  Dans une équation linéaire, l’erreur de prévision peut être divisée en 2 sous-particules. L’une est la déviance et l’autre est la différence. L’erreur de prévision peut être causée par ces deux composants ou par l’un ou l’autre.

  La régression de la souche résolve le problème de la collinearité multiple par le paramètre de contraction λ{\displaystyle \lambda } . Voir la formule suivante

  

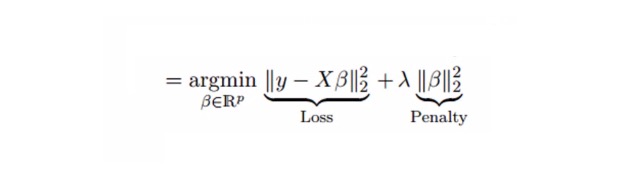
  Dans cette formule, il y a deux composantes. La première est le plus petit quadruple, et l’autre est le multiplicateur λ de β2 ((β-square), où β est le coefficient correspondant. Pour réduire le paramètre, on l’ajoute au plus petit quadruple pour obtenir une très faible différence.

  Le point:

  • Sauf en ce qui concerne les constantes, cette régression est similaire à celle de la régression minimale;
  • Il a réduit la valeur du coefficient pertinent, mais n’a pas atteint zéro, ce qui indique qu’il n’a pas de fonction de sélection de caractéristiques
  • C’est une méthode de régularisation qui utilise la régularisation L2.

• 6. La régression de Lasso

  Elle est similaire à la régression en cuivre, et Lasso (Least Absolute Shrinkage and Selection Operator) punit aussi la taille absolue du coefficient de régression. De plus, elle permet de réduire le degré de variation et d’améliorer la précision du modèle de régression linéaire. Voir la formule suivante:

  

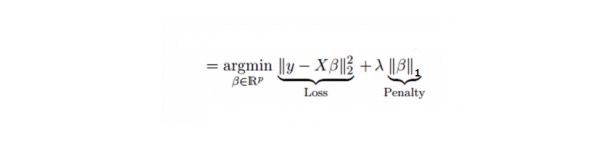
  La régression de Lasso diffère un peu de la régression de Ridge en ce qu’elle utilise une fonction de punition qui est une valeur absolue et non un carré. Cela entraîne que la punition (ou la somme des valeurs absolues de l’estimation contraignante) donne à certains paramètres une valeur d’estimation égale à zéro.

  Le point:

  • Sauf en ce qui concerne les constantes, cette régression est similaire à celle de la régression minimale;
  • Son coefficient de contraction est proche de zéro, ce qui contribue à la sélection des traits.
  • C’est une méthode de régularisation qui utilise la régularisation L1;
  • Si un ensemble de variables est hautement correlatif, Lasso choisit l’une d’entre elles et réduit les autres à zéro.

• 7. Retour à ElasticNet

  ElasticNet est un hybride des techniques de régression de Lasso et de Ridge. Il utilise L1 pour la formation et la priorité L2 comme matrice de normalisation. ElasticNet est utile lorsqu’il existe plusieurs traits associés.

  

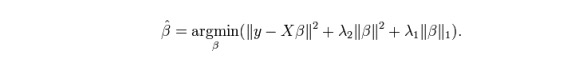
  L’avantage pratique entre Lasso et Ridge est qu’il permet à ElasticNet d’hériter de certaines de la stabilité de Ridge dans le cycle.

  Le point:

  • Dans le cas d’une variable hautement correlate, elle produit un effet de groupe;
  • Il n’y a pas de limite au nombre de variables à sélectionner.
  • Il résiste à la double contraction.
  • En plus des 7 techniques de régression les plus couramment utilisées, vous pouvez également consulter d’autres modèles, tels que la régression bayésienne, écologique et robuste.

• Comment choisir le bon modèle de régression ?

  La vie est souvent plus simple quand vous ne connaissez qu’une ou deux techniques. Un institut de formation que je connais a dit à ses étudiants d’utiliser la régression linéaire si les résultats sont séquentiels. Si c’est binaire, utilisez la régression logique! Cependant, plus il y a de choix dans notre traitement, plus il est difficile de choisir le bon.

  Dans un modèle de régression multivarié, il est important de choisir la technique la plus appropriée en fonction du type de variable et de variable, de la dimension des données et d’autres caractéristiques fondamentales des données. Voici les facteurs clés pour choisir le bon modèle de régression:

  L’exploration des données est une partie essentielle de la construction de modèles prédictifs. Elle devrait être la première étape dans le choix d’un modèle approprié, par exemple pour identifier les relations et les effets des variables.

  Il est possible d’analyser différents paramètres de l’indicateur, tels que les paramètres de signification statistique, R-square, Adjusted R-square, AIC, BIC et les termes d’erreur, l’autre étant la règle de Mallows’ Cp. Cela se fait principalement en comparant le modèle à tous les sous-modèles possibles (ou en les choisissant avec soin) et en examinant les écarts qui peuvent apparaître dans votre modèle.

  La validation croisée est la meilleure façon d’évaluer un modèle de prévision. Ici, divisez votre ensemble de données en deux parties (une pour la formation et l’autre pour la vérification).

  Si votre ensemble de données est composé de plusieurs variables mixtes, vous ne devriez pas choisir la méthode de sélection automatique du modèle, car vous ne devriez pas vouloir mettre toutes les variables dans le même modèle en même temps.

  Cela dépendra aussi de votre objectif. Il peut arriver qu’un modèle moins puissant soit plus facile à réaliser qu’un modèle à forte signification statistique.

  Les méthodes de régularisation de la régression ((Lasso, Ridge et ElasticNet) fonctionnent bien dans des situations de co-linéarité multiple entre les variables de haute dimension et de l’ensemble de données.

Une fois de plus, c’est la même chose.