Régression linéaire - méthode des moindres carrés

• ### Première préface

Pendant ce temps, j’ai appris à faire des exercices de mathématiques, j’ai appris la théorie de la régression logistique du chapitre 5, et cela m’a semblé assez difficile. J’ai fait le chemin du retour, de la théorie de la régression logistique à la théorie de la régression linéaire, puis à la théorie de la doublure minimale. J’ai finalement terminé dans la théorie de la doublure minimale du chapitre 9 du chapitre 10 de la théorie de la doublure minimale, ce qui explique d’où vient le principe mathématique derrière la théorie de la doublure minimale. Le casse-tête de la plus petite puissance est une mise en œuvre de la formule de l’expérience dans les problèmes d’optimisation. Savoir comment il fonctionne est utile pour comprendre le casse-tête de la régression logistique et le casse-tête de l’appui vectoriel.

• ### Deuxièmement, le contexte.

Le contexte historique de l’apparition du plus petit divisible par deux est intéressant.

En 1801, l’astronome italien Giuseppe Piazzi découvrit le premier astéroïde de la Voie Lactée. Après quarante jours d’observations de suivi, Piazzi perdit la position de la Voie Lactée en raison de son déplacement derrière le Soleil. Les scientifiques du monde entier utilisèrent ensuite les données d’observations de Piazzi pour commencer à chercher la Voie Lactée, mais sans résultat selon les résultats calculés par la plupart des gens.

La méthode utilisée par Gauss pour calculer le dixième de la moindre est publiée en 1809 dans son ouvrage La théorie du mouvement des corps célestes, tandis que le scientifique français Léger découvre de façon indépendante le dixième de la moindre en 1806, mais il n’en est pas question car il n’est pas connu de l’époque. Les deux hommes se disputent pour savoir qui a été le premier à créer le principe de la dixième de la moindre.

En 1829, Gauss fournit une preuve que l’optimisation de la multiplication par le plus petit nombre est plus efficace que les autres méthodes, voir le théorème de Gauss-Markov.

• ### Troisièmement, l’utilisation du savoir.

Le noyau de l’équation du plus petit carré est de garantir le carré et le plus petit de tous les écarts de données.

Supposons que nous ayons des données sur la longueur et la largeur de certains navires de guerre.

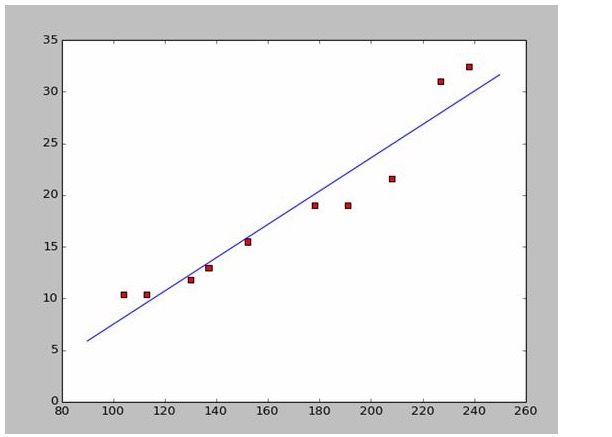
En utilisant Python, nous avons créé un diagramme de points de dispersion basé sur ces données:

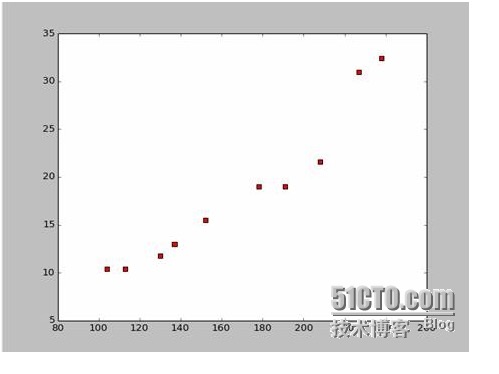
Voici le code de la carte à puces:

  import numpy as np                # -*- coding: utf-8 -*
  import os
  import matplotlib.pyplot as plt
  def drawScatterDiagram(fileName): # 改变工作路径到数据文件存放的地方
      os.chdir("d:/workspace_ml")
      xcord=[];ycord=[]
      fr=open(fileName)
      for line in fr.readlines():
          lineArr=line.strip().split()
          xcord.append(float(lineArr[1]));ycord.append(float(lineArr[2]))
      plt.scatter(xcord,ycord,s=30,c='red',marker='s')
      plt.show()

Si nous prenons les deux premiers points, 238, 32, 4 et 152, 15, 5, nous pouvons obtenir les deux équations. 152*a+b=15.5 328*a+b=32.4 Si on résolvait ces deux équations, on obtiendrait a = 0,197 et b = -14,48. Si nous avons une carte de l’équilibre, on obtient un diagramme de la même taille:

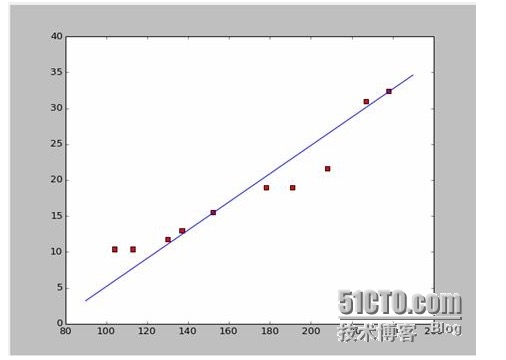
Bon, la nouvelle question est, est-ce que a et b sont des solutions optimales? Pour parler en termes professionnels, est-ce que a et b sont des paramètres d’optimisation du modèle? Avant de répondre à cette question, nous devons résoudre une autre question: quelles conditions a et b satisfont le mieux?

La réponse est: le carré et le plus petit de tous les écarts de données garantis. Quant au principe, nous le verrons plus loin pour voir comment utiliser cet outil pour calculer le meilleur a et b. En supposant que le carré de toutes les données soit M,

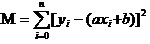
Maintenant, nous allons trouver le plus petit a et le plus petit b de M. Notez que dans cette équation, nous avons déjà y et xi.

Alors cette équation est une fonction binaire avec a, b comme variable propre et M comme variable cause.

Rappelons que la fonction unitaire est extrême dans les nombres élevés. Nous utilisons un instrument appelé la dérivée. Dans les fonctions binaires, nous utilisons toujours la dérivée. En appliquant la partielle à M, on obtient un ensemble d’équations.

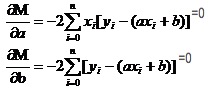
Dans les deux équations, on connaît les valeurs de xi et de y.

Il est facile d’obtenir a et b. En utilisant les données de Wikipédia, j’utilise directement les réponses pour dessiner une image appropriée:

  # -*- coding: utf-8 -*importnumpy as npimportosimportmatplotlib.pyplot as pltdefdrawScatterDiagram(fileName):
  # 改变工作路径到数据文件存放的地方os.chdir("d:/workspace_ml")xcord=[];
  # ycord=[]fr=open(fileName)forline infr.readlines():lineArr=line.strip().split()xcord.append(float(lineArr[1]));
  # ycord.append(float(lineArr[2]))plt.scatter(xcord,ycord,s=30,c='red',marker='s')
  # a=0.1965;b=-14.486a=0.1612;b=-8.6394x=np.arange(90.0,250.0,0.1)y=a*x+bplt.plot(x,y)plt.show()
  # -*- coding: utf-8 -*
  import numpy as np
  import os
  import matplotlib.pyplot as plt
  def drawScatterDiagram(fileName):
      #改变工作路径到数据文件存放的地方
      os.chdir("d:/workspace_ml")
      xcord=[];ycord=[]
      fr=open(fileName)
      for line in fr.readlines():
          lineArr=line.strip().split()
          xcord.append(float(lineArr[1]));ycord.append(float(lineArr[2]))
      plt.scatter(xcord,ycord,s=30,c='red',marker='s')
      #a=0.1965;b=-14.486
      a=0.1612;b=-8.6394
      x=np.arange(90.0,250.0,0.1)
      y=a*x+b
      plt.plot(x,y)
      plt.show()

• ### Quatre principes à explorer

Dans l’appariement des données, pourquoi optimiser les paramètres du modèle par le carré de la différence entre les données de prévision du modèle et les données réelles plutôt que par la valeur absolue et la valeur minimale ?

Cette question a déjà été posée, voir le lien (http://blog.sciencenet.cn/blog-430956-621997).

Personnellement, je trouve cette explication très intéressante. En particulier l’hypothèse: tous les points qui s’écartent de f (x) sont bruyants.

Un point d’écart plus éloigné signifie que plus le bruit est fort, plus la probabilité qu’il se produise est faible. Quel est le rapport entre l’écart x et la probabilité d’apparition f (x)?

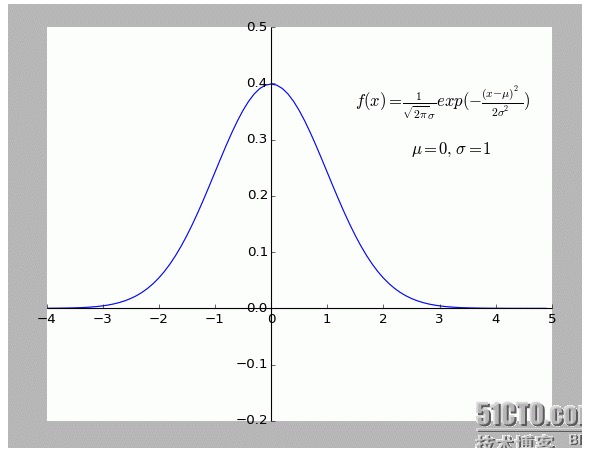
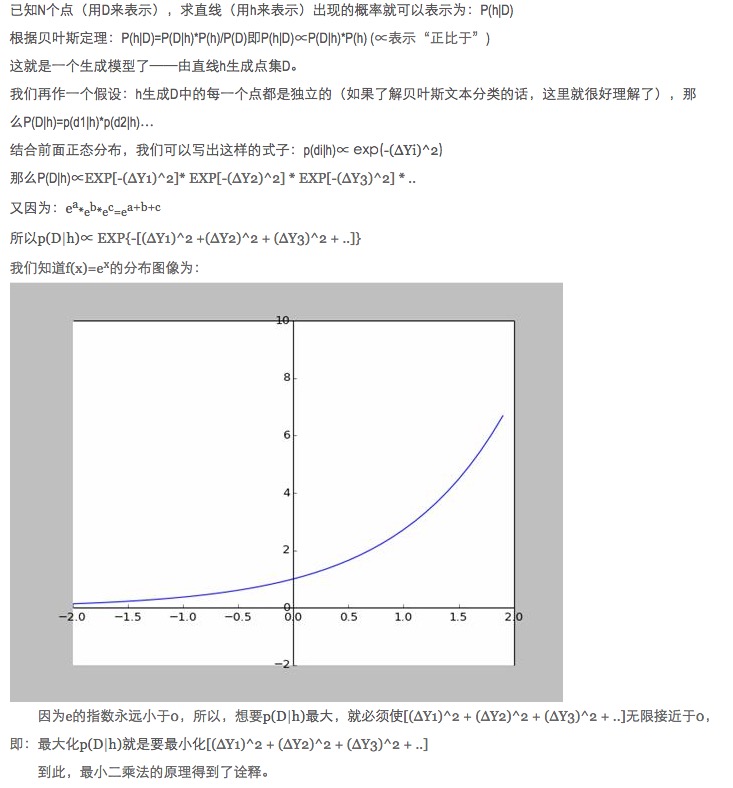
• ### Cinquièmement, élargir et étendre

Les situations décrites ci-dessus sont bidimensionnelles, c’est-à-dire qu’il n’y a qu’une seule variable autonome. Cependant, dans le monde réel, la superposition de plusieurs facteurs qui influencent le résultat final, c’est-à-dire qu’il y a plusieurs variables autonomes.

Pour les fonctions métalliques N en général, l’inverse de la matrice dans la colonne de l’algèbre linéaire est acceptable; comme nous n’avons pas trouvé d’exemple approprié pour le moment, nous le laisserons ici comme argument.

Bien sûr, la nature est beaucoup plus polyvalente qu’elle n’est simplement linéaire, c’est plus avancé.

• Références

  • Mathématiques de l’enseignement supérieur (sixième édition)
  • Algebra linéaire conique (Publication de l’Université de Pékin)
  • Il y a aussi une encyclopédie interactive:Le plus petit carré
  • Wikipédia: Le plus petit carré
  • Le réseau scientifique:Le plus petit carré ? Une valeur absolue qui n’est pas mauvaise pour un cheval de dieu

Les œuvres originales, les reproductions autorisées, les reproductions doivent être accompagnées d’un lien hypertexte indiquant la source de l’article, les informations sur l’auteur et la présente déclaration. Sinon, la responsabilité légale sera engagée. http://sbp810050504.blog.51cto.com/2799422/1269572