Compréhension intéressante de la théorie naïve de Bayes

NavieBayes

  Il existe de nombreux cas d’utilisation de la classification dans la vie quotidienne, tels que la classification de l’actualité, la classification des patients, etc. Afin de permettre une compréhension visuelle, cet article présente un algorithme de classification simple et couramment utilisé à partir d’applications pratiques: le classificateur Navie Bayes.

• 01 Exemple de catégorisation des patients

Laissez-moi commencer par un exemple, vous verrez que le classificateur de Bayes est facile à comprendre, pas difficile du tout. Un hôpital a reçu six patients en consultation le matin, comme le montre le tableau suivant.

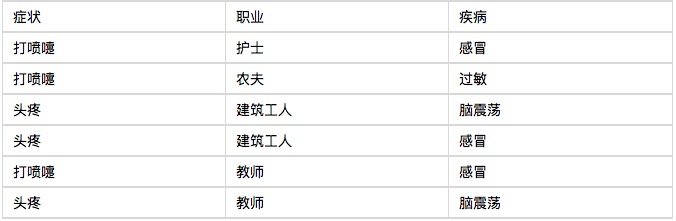
Le septième patient, un ouvrier du bâtiment qui crache, demandez-lui quelle est la probabilité qu’il ait attrapé un rhume.

  P(A|B) = P(B|A) P(A) / P(B)

Je ne sais pas.

  P(感冒|打喷嚏x建筑工人) 
  　　　　= P(打喷嚏x建筑工人|感冒) x P(感冒) 
  　　　　/ P(打喷嚏x建筑工人)

En supposant que les caractéristiques de “sniffer” et de “constructeur” soient indépendantes, l’équation ci-dessus devient

  P(感冒|打喷嚏x建筑工人) 
  　　　　= P(打喷嚏|感冒) x P(建筑工人|感冒) x P(感冒)
  　　　　/ P(打喷嚏) x P(建筑工人)

C’est calculé.

  P(感冒|打喷嚏x建筑工人) 
  　　　　= 0.66 x 0.33 x 0.5 / 0.5 x 0.33 
  　　　　= 0.66

Ainsi, il y a 66% de chances que ce travailleur ait eu un rhume. On peut aussi calculer la probabilité qu’il ait eu une allergie ou une commotion cérébrale. En comparant ces probabilités, on peut déterminer quelle est la maladie la plus probable.

C’est la méthode de base du classificateur de Bayes: calculer la probabilité de chaque catégorie en fonction de certaines caractéristiques, sur la base de données statistiques, pour réaliser la classification.

• 02 Formule du classificateur simple de Bayes

Supposons qu’un individu possède n caractéristiques, soit respectivement F1, F2, … , Fn. Il existe m catégories, soit respectivement C1, C2, … , Cm. Le classificateur de Bayes est la classification qui permet de calculer la plus grande probabilité, c’est-à-dire la valeur maximale de l’algorithme suivant:

  P(C|F1F2...Fn) 
  　　   = P(F1F2...Fn|C)P(C) / P(F1F2...Fn)

Puisque P ((F1F2…Fn) est le même pour toutes les catégories, on peut l’omettre et la question devient

  P(F1F2...Fn|C)P(C)

La valeur maximale de

Le classificateur simpliste de Bayes va plus loin, en supposant que toutes les caractéristiques sont indépendantes les unes des autres, et donc

  P(F1F2...Fn|C)P(C) 
  　　   = P(F1|C)P(F2|C) ... P(Fn|C)P(C)

Chaque élément de la droite de l’équation peut être obtenu à partir des données statistiques, permettant de calculer la probabilité de correspondance de chaque catégorie, et ainsi de trouver la catégorie la plus probable.

Bien que l’hypothèse selon laquelle “toutes les caractéristiques sont indépendantes les unes des autres” soit peu probable dans la réalité, elle simplifie considérablement le calcul et certaines études ont montré qu’elle n’avait pas d’impact significatif sur l’exactitude des résultats de la classification.

Voici deux autres exemples d’utilisation du classificateur simple de Bayes:

• 03 Classification des comptes

Selon un échantillon de statistiques d’un site communautaire, 89% des 10 000 comptes de ce site sont des vrais comptes (C0), 11% sont des faux comptes (C1). Ensuite, les statistiques sont utilisées pour juger de la véracité d’un compte.

  C0 = 0.89 C1 = 0.11

Supposons qu’un compte présente les trois caractéristiques suivantes: F1: Nombre de journaux/nombre de jours d’enregistrement F2: Nombre d’amis / nombre de jours d’inscription F3: Utilisez-vous une image réelle (une image réelle est 1, une image non réelle est 0)? F1 = 0.1  F2 = 0.2  F3 = 0

Pour savoir si le compte est réel ou faux, utilisez un classificateur simple de Bayes et calculez la valeur de la formule suivante:

P(F1|C)P(F2|C)P(F3|C)P©

Bien que les valeurs ci-dessus puissent être obtenues à partir des statistiques, il y a un problème: F1 et F2 sont des variables continues, il n’est pas approprié de calculer la probabilité en fonction d’une valeur donnée. Une astuce consiste à convertir une valeur continue en une valeur disjointe, calculer la probabilité d’un intervalle.[0, 0.05]、(0.05, 0.2)、[0.2, +∞] trois intervalles, puis calculer la probabilité de chaque intervalle. Dans notre exemple, F1 est égal à 0.1, tombant dans le deuxième intervalle, donc la probabilité de l’occurrence du deuxième intervalle est utilisée pour le calcul.

Selon les statistiques:

P(F1|C0) = 0.5, P(F1|C1) = 0.1  P(F2|C0) = 0.7, P(F2|C1) = 0.2  P(F3|C0) = 0.2, P(F3|C1) = 0.9

Donc

P(F1|C0) P(F2|C0) P(F3|C0) P(C0)  = 0.5 x 0.7 x 0.2 x 0.89  = 0.0623 P(F1|C1) P(F2|C1) P(F3|C1) P(C1)  = 0.1 x 0.2 x 0.9 x 0.11  = 0.00198 On peut voir que, bien que l’utilisateur n’ait pas utilisé de photo d’identité réelle, il est plus de 30 fois plus probable qu’il s’agisse d’un compte réel que d’un faux, ce qui justifie qu’il s’agisse d’un compte authentique.

• 04 Catégorie par sexe

Voici un ensemble de statistiques sur les caractéristiques du corps humain.

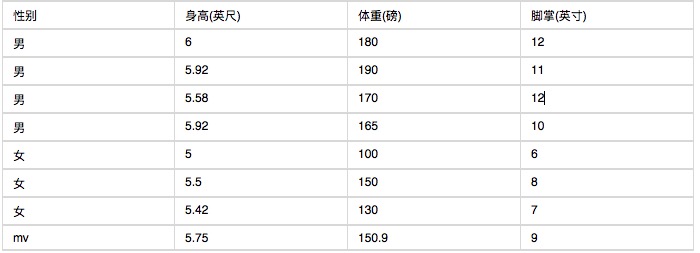
Si vous connaissez quelqu’un de 6 pieds, 130 livres et 8 pouces, demandez-lui s’il s’agit d’un homme ou d’une femme. Calculez la valeur de la formule ci-dessous en utilisant le classificateur de Bayes naïf.

P (hauteur et sexe) x P (poids et sexe) x P (pouce et sexe) x P (sexe)

La difficulté réside dans le fait qu’étant donné que la taille, le poids et la paume sont des variables continues, il n’est pas possible de calculer la probabilité en utilisant une méthode de variables discrètes. Et comme il y a trop peu d’échantillons, il n’est pas possible de les diviser en intervalles.

Avec ces données, il est possible de calculer la classification par sexe.

P (taille = 6 ans) x P (poids = 130 ans) x P (paume = 8 ans) x P (homme)

= 6.1984 x e-9

P (hauteur = 6 filles) x P (poids = 130 filles) x P (paume = 8 filles) x P (femme)

= 5.3778 x e-4

Comme on peut le voir, les femmes sont presque 10 000 fois plus susceptibles que les hommes d’être considérées comme des femmes.

Le numéro public de Weibo de Weibo depuis le sommet de Yan’an