Modèle de Markov caché

• ### La connaissance

Aujourd’hui, nous allons vous présenter une application simple du HMM dans les actions.

Le modèle de Markov, qui semble très sophistiqué à première vue, n’a aucune idée de ce que c’est, alors faisons un pas en arrière et regardons la chaîne de Markov.

Les chaînes de Markov, nommées d’après André Markov (A.A. Markov, 1856-1922) sont des processus aléatoires d’événements dissociés qui ont une nature markoviste en mathématiques. Dans le cas d’une connaissance ou d’une information actuelle donnée, le passé (c’est-à-dire l’état historique antérieur au présent) n’est pas pertinent pour prédire l’avenir (c’est-à-dire l’état futur postérieur au présent).

Dans ce processus, chaque transition d’un état dépend uniquement des n états précédents, ce processus est appelé un modèle à 1 n degrés, où n est le nombre d’états affectés par la transition. Le processus de Markov le plus simple est un processus à un degré, chaque transition d’un état dépendant uniquement de l’état précédent.

• ### Deuxième exemple

L’expression mathématique est la suivante:

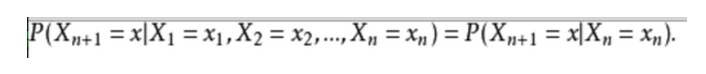
Pour prendre un exemple de la vie quotidienne, nous voulons prédire la météo à l’avenir en fonction de la météo actuelle. Une façon de le faire est de supposer que chaque état de ce modèle dépend uniquement de l’état précédent, l’hypothèse de Markov, qui simplifie considérablement le problème. Bien sûr, cet exemple est quelque peu irréaliste. Cependant, un tel système de simplification peut être bénéfique pour notre analyse, et nous acceptons généralement de telles hypothèses parce que nous savons qu’un tel système peut nous donner des informations utiles, bien que pas très précises.

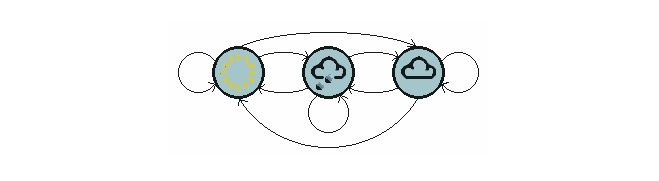
Le graphique ci-dessus montre un modèle de météo transférée.

Notez qu’un processus de phase 1 contenant N états a N 2 transitions d’état. La probabilité de chaque transition est appelée probabilité de transition d’état, c’est-à-dire la probabilité de passer d’un état à un autre. Toutes ces N 2 probabilités peuvent être représentées par une matrice de transition d’état, la matrice de transition d’état de l’exemple météorologique ci-dessus est la suivante:

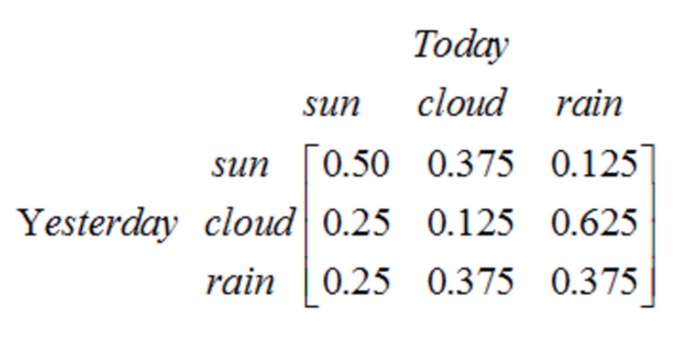
Cette matrice indique qu’il y a une probabilité de 25% qu’il soit clair aujourd’hui, une probabilité de 12.5% qu’il soit nuageux et une probabilité de 62.5% qu’il pleuve si hier il y a eu un jour de neige. Il est évident que la somme de chaque ligne de la matrice est de 1 .

Pour initialiser un tel système, nous avons besoin d’un vecteur de probabilité initiale:

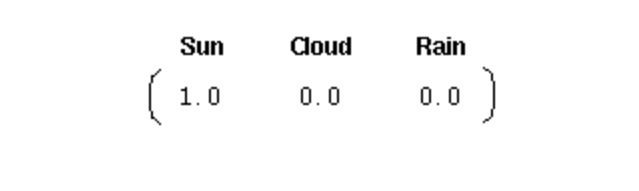
Ce vecteur indique que le premier jour est un jour de beau temps. Ici, nous définissons les trois parties suivantes pour le processus de Markov du premier degré ci-dessus:

Les conditions météorologiques sont les suivantes: beau jour, nuageux et pluvieux.

Vecteur initial: définit la probabilité de l’état du système au moment où le temps est égal à 0.

Matrice de transition d’état: probabilité de chaque transition météorologique. Tous les systèmes pouvant être décrits de cette façon sont des processus de Markov.

Cependant, que faire quand le processus de Markov n’est pas assez puissant ? Dans certains cas, le processus de Markov ne suffit pas à décrire les modèles que nous souhaitons découvrir.

Par exemple, si nous observons le marché boursier, nous ne pouvons connaître que les prix, le volume, etc. du jour, mais nous ne savons pas dans quel état se trouve le marché boursier actuel (bull market, bear market, oscillation, rebond, etc.), dans ce cas nous avons deux ensembles d’états, un ensemble d’états observables (prix boursier, volume boursier, etc.) et un ensemble d’états cachés (état du marché boursier). Nous souhaitons trouver un algorithme qui puisse prédire l’état du marché boursier en fonction de l’état du marché boursier et de l’hypothèse de Markov.

Dans les cas ci-dessus, les séquences d’états observables et les séquences d’états cachés sont probabilisées. On peut donc modéliser ce type de processus comme ayant un processus de Markov caché et un ensemble d’états observables et liés à cette probabilité de processus de Markov caché, le modèle de Markov caché.

Le modèle de Markov caché est un modèle statistique utilisé pour décrire un processus de Markov contenant des paramètres inconnus implicites. La difficulté consiste à déterminer les paramètres implicits du processus à partir des paramètres observables, puis à utiliser ces paramètres pour une analyse ultérieure.

Prenons l’exemple d’un couteau. Supposons que nous ayons trois couleurs différentes. La première couleur est celle que nous connaissons habituellement (appelons ce couteau D6), avec 6 faces, chacune avec 1, 2, 3, 4, 5, 6) et la probabilité d’apparaître est de ¹⁄₆. La deuxième couleur est un quadrilatère (appelons ce couteau D4) et chaque face 1, 2, 3, 4) avec ¹⁄₄ de probabilité.

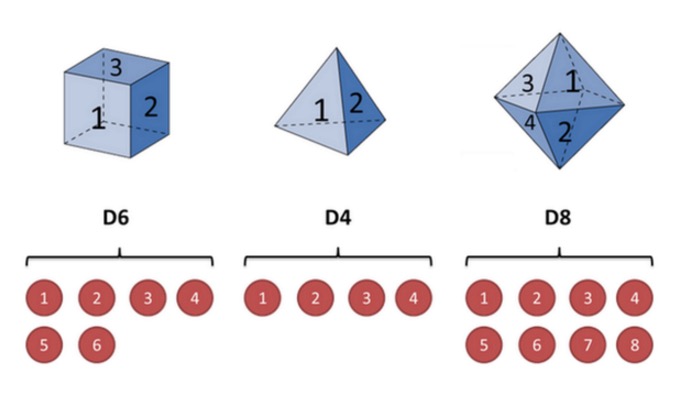
Supposons que nous commencions le tirage au sort en choisissant un tirage au sort parmi les trois tirages, et que la probabilité de choisir un tirage au sort est de ¹⁄₃. Ensuite, nous tirons au sort, et nous obtenons un nombre, 1, 2, 3, 4, 5, 6, 7, 8. En répétant sans cesse le processus ci-dessus, nous obtenons une série de nombres, chaque nombre étant un tirage au sort parmi 1, 2, 3, 4, 5, 6, 7, 8.

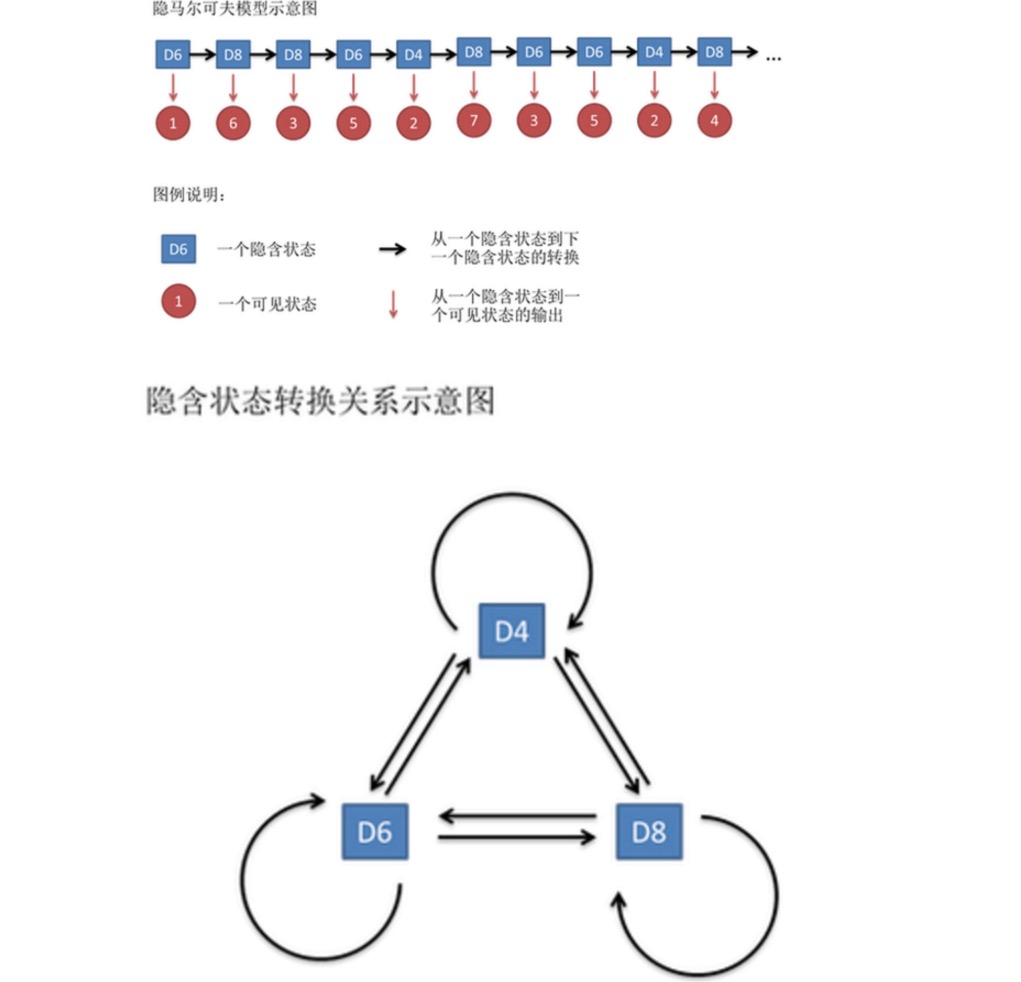
Cette chaîne de chiffres est appelée chaîne d’état visible. Mais dans le modèle de Markov latent, nous avons non seulement cette chaîne d’état visible, mais aussi une chaîne d’état implicite. Dans cet exemple, la chaîne d’état implicite est la séquence de chaînes que vous utilisez. Par exemple, la chaîne d’état implicite pourrait être:

En général, la chaîne de Markov mentionnée dans le HMM est en fait une chaîne d’état latent, car il existe une probabilité de conversion entre les états latents ((le crochet)). Dans notre exemple, le prochain état de D6 est D4, D6, D8 avec une probabilité de 1 / 3. D4, D8 avec D4, D6, D8 avec une probabilité de conversion de 1 / 3.

De même, bien qu’il n’y ait pas de probabilité de conversion entre les états visibles, il y a une probabilité entre les états implicites et les états visibles appelée probabilité de sortie. Dans notre exemple, la probabilité de sortie d’une souris à six faces (D6) est ¹⁄₆. La probabilité de sortie d’une souris à six faces (D6) est ¹⁄₆.

En fait, pour les HMM, il est assez facile de faire des simulations si vous connaissez à l’avance la probabilité de conversion entre tous les états cachés et la probabilité de sortie entre tous les états cachés et tous les états visibles. Cependant, lorsque vous appliquez un modèle HMM, une partie de l’information est souvent manquante. Parfois, vous savez combien de nœuds il y a et ce que chaque nœud est, mais vous ne savez pas la séquence de nœuds qui en résulte.

Les algorithmes liés au modèle HMM sont principalement divisés en trois catégories, qui résolvent respectivement trois types de problèmes:

• Sachant combien de nœuds il y a (nombre d’états cachés), ce que chaque nœud est (probabilité de conversion), en fonction du résultat du nœud (chaîne d’état visible), je veux savoir quel nœud est sorti à chaque fois (chaîne d’état caché).

• Je sais combien de chaînes il y a (nombre d’états implicites), quelle est la probabilité de chaque chaîne (probabilité de conversion), et quelle est la probabilité de cette réponse (chaîne d’états visibles) en fonction du résultat de la chaîne.

• Sachant combien de chaînes il y a ((nombre d’états implicites), ne sachant pas ce que chaque chaîne est ((probabilité de conversion), observant les résultats de nombreuses chaînes ((chaîne d’états visibles), j’aimerais répéter ce que chaque chaîne est ((probabilité de conversion) }}.

  Si nous voulons résoudre le problème de la bourse, nous devons résoudre les problèmes 1 et 3 et nous verrons comment le faire dans le prochain article.

Partagé par le blog Unknown Moneycode