Kurtosis et Skewness (Aplatissement et asymétrie)

• #### La courtoisie et la squeletticité

Article publié par EasyTrader

Il s’agit d’une stratégie de trading basée sur la courtosis et la skewness des données statistiques. Lorsque les données sont tendances et que la tendance potentielle est positive, nous faisons plus. Lorsque les données sont tendances et que la tendance potentielle est négative, nous faisons moins.

Alors, comment pouvons-nous déterminer la tendance et la force de la tendance ?

Tout d’abord, la définition d’une distribution normale

Distribution: situation de distribution dans laquelle toutes les valeurs de la variable apparaissent le plus souvent, avec les valeurs de la variable sur l’axe horizontal et la fréquence d’apparition sur l’axe vertical. Distribution normale: aussi appelée distribution gaussienne

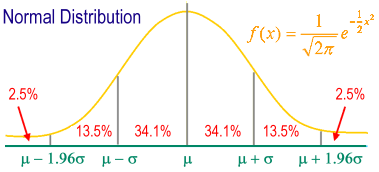
Distribution normale standard: diagramme de distribution normale représentant la moyenne au centre et la déviation standard comme unité de base de l’axe de la jauge. Symétrique en forme de cloche.

m ± 1s contient 68,26% des individus de l’ensemble de l’échantillon.

m ± 2s contient 95,44% des individus de l’ensemble du groupe échantillon.

m ± 3s contient 99,74% des individus de l’ensemble du groupe échantillon.

95% des individus sont situés entre m ± 1.96s.

99% des individus sont tombés entre m ± 2.58s.

En statistique, la courtoisie mesure le pic de la distribution des probabilités d’une variable aléatoire réelle. Une courtoisie élevée signifie que l’augmentation de la variance est causée par une variance extrême plus grande ou plus petite que la moyenne à basse fréquence.

La courtosis est une mesure statistique du degré de courbure de la distribution d’un ensemble de données. La courbure de la distribution normale est de 3, donc nous appelons la courbure supérieure à 3 la courbure, indiquant que la distribution est plus concentrée et plus harmonieuse que la distribution normale. Nous appelons la courbure inférieure à 3 la courbure plane, indiquant que la distribution est plus lisse que la distribution positive.

La skewness décrit la symétrie de la distribution des données, ou la position du nombre de données dans le mode. Une skewness égale à 0 décrit une symétrie parfaite. Cette statistique nécessite également une comparaison avec la distribution normale: une skewness supérieure à 0 indique que, par rapport à la distribution normale, l’array présente un décalage vers la droite, représentant une longue traîne à droite et une valeur extrême plus probable à la droite; au contraire, une skewness vers la gauche, représentant une longue traîne à gauche et une valeur extrême plus probable à la gauche.

En théorie des probabilités et en statistique, l’égarement mesure l’asymétrie de la distribution des probabilités de variables aléatoires réelles. Les valeurs d’égarement peuvent être positives, négatives ou même indéfinissables. Quantitativement, l’égarement négatif signifie que la longueur de l’extrémité gauche de la fonction de densité de probabilité est supérieure à celle de la droite, la grande majorité des valeurs (y compris la moyenne) étant situées à droite de la moyenne.

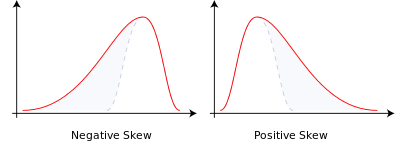
Il y a deux types de préjugés:

• Paré négatif ou paré gauche: la queue de gauche est plus longue et le corps principal de la distribution est concentré sur le côté droit.
• Poitrine polarisée ou poitrine droite: la queue de droite est plus longue et le corps principal de la distribution est concentré sur la gauche.
• Si la distribution est symétrique, alors la moyenne est égale à la médiane, et l’anomalie est égale à zéro (en outre, si la distribution est une distribution à un seul sommet, alors la moyenne est égale à la médiane et la variance est égale à la variance).

• Nous avons donc déduit les règles suivantes: lorsque le pic est inférieur à 0 (le marché est en tendance), l’écart est supérieur à N (la tendance est à la hausse), faites plus; Lorsque le pic est inférieur à 0 (le marché est en tendance), l’écart est inférieur à M (la tendance est à la baisse), le shorting;

MATLAB: les personnes intéressées peuvent faire un essai de conversion en JS.

input:ExitType(5) ;
input:NBarL(2),NBarS(2),TradeProfit(0.053),TradeStopLoss(0.023),ATRs_L(5.4),ATRs_S(10.9);
vars: IsBalanceDay(False),MP(0),PF(0),PL(0),HLRange(100);

inputs:Length(20),Trigger(3),UpSkew(3.4),DownSkew(2.2) ;
vars:KurtValue(0),SkewValue(0),BuyPoint(0),SellPoint(0);

MP = MarketPosition ;
if DAYofMonth(Date) > 14 and DAYofMonth(Date) < 22 and DAYofWeek(Date)= 3 then isBalanceDay = True else isBalanceDay =False ;

PF = AvgPrice*TradeProfit ;
PL = AvgPrice*TradeStopLoss ;

{计算峰度 }
KurtValue = Kurtosis(Close,Length) ;
{计算偏度}
SkewValue = Skew(Close,Length) ;

{ 峰度向下跌破 Trigger 线 ,建立买卖点 }
if KurtValue Cross under Trigger then Begin
BuyPoint = High 3;
SellPoint = Low-3;
end;

{ 偏度大于某数值后 ,趋势确认进场作多 }
if  SkewValue > -UpSkew 2 then Buy next bar at BuyPoint stop ;
{ 偏度小于某数值后 ,趋势确认进场作空 }
if  SkewValue < -DownSkew 2 then Sell next bar at SellPoint Stop ;
end;

if ExitType = 1 then SetStopLoss(PL * BigPointValue) ;

if ExitType = 2 then Begin
SetStopLoss(PL * BigPointValue) ;
setProfitTarget(PF * BigPointValue) ;
end;

if ExitType = 3 then Begin
if MP > 0 and BarsSinceEntry = NBarL then ExitLong next bar at Market ;
if MP < 0 and BarsSinceEntry = NBarS then ExitShort next bar at Market ;
end;

if ExitType = 4 then Begin
SetStopLoss(PL * BigPointValue) ;
setProfitTarget(PF * BigPointValue) ;
if MP > 0 and BarsSinceEntry = NBarL then {Sell } ExitLong next bar at Market ;
if MP < 0 and BarsSinceEntry = NBarS then {Buy} ExitShort next bar at Market ;
end;

if ExitType = 5 then Begin
{*******************************************************************
Description : ATR Trailing Stop Long Exit
Provided By : Omega Research, Inc. (c) Copyright 1999
********************************************************************}
{Inputs: ATRs_L(3);}
Variables: PosHigh(0), ATRVal_L(0);

ATRVal_L = AvgTrueRange(10) * ATRs_L;
If BarsSinceEntry = 0 Then PosHigh = High;
If MarketPosition = 1 Then Begin
If High > PosHigh Then PosHigh = High;
ExitLong ("ATR") Next Bar at PosHigh - ATRVal_L Stop;
End else ExitLong ("ATR eb") Next bar at High - ATRVal_L Stop;

{*******************************************************************
Description : ATR Trailing Stop Short Exit
Provided By : Omega Research, Inc. (c) Copyright 1999
******************************************************************}
{Inputs: ATRs_S(3);}
Variables: PosLow(0), ATRVal_S(0);

ATRVal_S = AvgTrueRange(10) * ATRs_S;
If BarsSinceEntry = 0 Then PosLow = Low;
If MarketPosition = -1 Then Begin
If Low < PosLow Then PosLow = Low;
ExitShort ("ATR_1") Next Bar at PosLow ATRVal_S Stop;
End else ExitShort ("ATR_1 eb") Next bar at Low ATRVal_S Stop;
end;

if IsBalanceDay then setExitonClose ;

Le blog de Faruto a été publié en anglais.