Réflexions sur les stratégies de trading haute fréquence (1)
 3
3
 4856
4856

L’article traite des stratégies de trading haute fréquence des monnaies numériques, y compris les sources de bénéfices (principalement provenant des fluctuations du marché et des remises sur les frais de change), les problèmes de passation d’ordres et de contrôle des positions, ainsi que la méthode de modélisation du volume des transactions à l’aide de la distribution de Pareto. En outre, les données de transaction et d’ordre optimal fournies par Binance ont été utilisées pour le backtesting, et d’autres questions relatives aux stratégies de trading haute fréquence devraient être discutées en profondeur dans des articles ultérieurs.
J’ai déjà écrit deux articles sur le trading haute fréquence de devises numériques. Une introduction détaillée aux stratégies à haute fréquence pour les monnaies numériques, Gagnez 80 fois en 5 jours, la puissance de la stratégie à haute fréquence. Mais cela ne peut être considéré que comme un partage d’expérience et une discussion générale. Cette fois, je prévois d’écrire une série d’articles pour présenter les idées du trading haute fréquence dès le début. J’espère être aussi concis et clair que possible. Cependant, en raison de mon niveau limité et de ma compréhension approfondie du trading haute fréquence, trading, cet article n’est qu’un point de départ. J’espère que les experts pourront me corriger.
Sources de profit à haute fréquence
Comme mentionné dans les articles précédents, les stratégies à haute fréquence sont particulièrement adaptées aux marchés présentant des hauts et des bas extrêmement volatils. Examinez les variations de prix d’un produit commercial sur une courte période de temps, qui comprend les tendances et les fluctuations générales. Si nous pouvons prédire avec précision les changements de tendances, nous pouvons certainement gagner de l’argent, mais c’est aussi le plus difficile. Cet article présente principalement les stratégies des créateurs de haute fréquence et n’abordera pas ce problème. Dans un marché volatil, si la stratégie de placement d’ordres à la hausse et à la baisse est exécutée suffisamment fréquemment et que la marge bénéficiaire est suffisamment importante, elle peut couvrir les pertes éventuelles causées par la tendance, de sorte que vous pouvez réaliser un profit sans prédire le marché. Actuellement, toutes les transactions des créateurs sur les bourses bénéficient de remises sur les frais de transaction, qui constituent également une composante du bénéfice. Plus la concurrence est intense, plus la proportion de remises doit être élevée.
Problème à résoudre
La stratégie place des ordres d’achat et des ordres de vente en même temps. La première question est de savoir où placer les ordres. Plus l’ordre est proche du marché, plus la probabilité d’une transaction est élevée. Cependant, dans un marché volatil, le prix instantané de la transaction peut être très éloigné du marché. Si l’ordre est placé trop près, vous ne pourrez pas obtenir suffisamment de profit. La probabilité d’exécution d’ordres passés trop loin est faible. C’est un problème qui doit être optimisé.
Contrôlez votre position. Afin de contrôler les risques, la stratégie ne peut pas accumuler trop de positions pendant une longue période. Cela peut être résolu en contrôlant la distance de commande, la quantité commandée, la limite de position totale, etc.
Pour atteindre les objectifs ci-dessus, il est nécessaire de modéliser et d’estimer la probabilité de transaction, le profit de la transaction, l’estimation du marché et d’autres aspects. Il existe de nombreux articles et documents dans ce domaine, qui peuvent être trouvés avec des mots-clés tels que Trading haute fréquence , Carnet de commandes, etc. Il existe de nombreuses recommandations en ligne, sur lesquelles je ne m’étendrai pas ici. De plus, il est préférable de mettre en place un système de backtesting fiable et rapide. Bien que les stratégies à haute fréquence puissent être facilement vérifiées par le biais de transactions réelles pour vérifier leur efficacité, le backtesting peut toujours fournir plus d’idées et réduire le coût des essais et des erreurs.
Données requises
Binance fournit des données transaction par transaction et des données de meilleur ordretéléchargerLes données profondes doivent être téléchargées à l’aide de l’API dans la liste blanche, ou vous pouvez les collecter vous-même. À des fins de backtesting, vous pouvez simplement utiliser les données de transaction collectées. Cet article prend les données de HOOKUSDT-aggTrades-2023-01-27 comme exemple.
from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
Les colonnes d’une transaction sont les suivantes :
- agg_trade_id : l’identifiant de l’ordre de transaction agrégé,
- Prix : prix de transaction
- Quantité : Le nombre de transactions
- first_trade_id : Il peut y avoir plusieurs transactions dans la collection en même temps, une seule donnée est comptabilisée, c’est l’identifiant de la première transaction
- last_trade_id : l’identifiant de la dernière transaction
- transact_time : heure de la transaction
- is_buyer_maker : sens de la transaction, True signifie que l’ordre d’achat est négocié par le créateur et que l’ordre de vente est négocié par le preneur
On peut voir qu’il y a eu 660 000 données de transaction ce jour-là, et les transactions étaient très actives. Le csv sera joint dans la section commentaires.
trades = pd.read_csv('COMPUSDT-aggTrades-2023-07-02.csv')
trades
664475 rows × 7 columns
| agg_trade_id | price | quantity | first_trade_id | last_trade_id | transact_time | is_buyer_maker |
|---|---|---|---|---|---|---|
| 120719552 | 52.42 | 22.087 | 207862988 | 207862990 | 1688256004603 | False |
| 120719553 | 52.41 | 29.314 | 207862991 | 207863002 | 1688256004623 | True |
| 120719554 | 52.42 | 0.945 | 207863003 | 207863003 | 1688256004678 | False |
| 120719555 | 52.41 | 13.534 | 207863004 | 207863006 | 1688256004680 | True |
| … | … | … | … | … | … | … |
| 121384024 | 68.29 | 10.065 | 210364899 | 210364905 | 1688342399863 | False |
| 121384025 | 68.30 | 7.078 | 210364906 | 210364908 | 1688342399948 | False |
| 121384026 | 68.29 | 7.622 | 210364909 | 210364911 | 1688342399979 | True |
Modélisation du volume de transactions uniques
Tout d’abord, traitez les données et divisez les transactions d’origine en groupe de transactions actives d’ordre d’achat et en groupe de transactions actives d’ordre de vente. En outre, les données de transaction agrégées d’origine sont un élément de données au même moment, au même prix et dans la même direction. Il peut y avoir un ordre d’achat actif avec un volume de 100. S’il est divisé en plusieurs transactions avec des prix, tels que 60 et 40, deux éléments de données seront générés, affectant l’estimation du volume de l’ordre d’achat. Il est donc nécessaire d’agréger à nouveau en fonction de transact_time. Après agrégation, la quantité de données a été réduite de 140 000 enregistrements.
trades['date'] = pd.to_datetime(trades['transact_time'], unit='ms')
trades.index = trades['date']
buy_trades = trades[trades['is_buyer_maker']==False].copy()
sell_trades = trades[trades['is_buyer_maker']==True].copy()
buy_trades = buy_trades.groupby('transact_time').agg({
'agg_trade_id': 'last',
'price': 'last',
'quantity': 'sum',
'first_trade_id': 'first',
'last_trade_id': 'last',
'is_buyer_maker': 'last',
'date': 'last',
'transact_time':'last'
})
sell_trades = sell_trades.groupby('transact_time').agg({
'agg_trade_id': 'last',
'price': 'last',
'quantity': 'sum',
'first_trade_id': 'first',
'last_trade_id': 'last',
'is_buyer_maker': 'last',
'date': 'last',
'transact_time':'last'
})
buy_trades['interval']=buy_trades['transact_time'] - buy_trades['transact_time'].shift()
sell_trades['interval']=sell_trades['transact_time'] - sell_trades['transact_time'].shift()
print(trades.shape[0] - (buy_trades.shape[0]+sell_trades.shape[0]))
146181
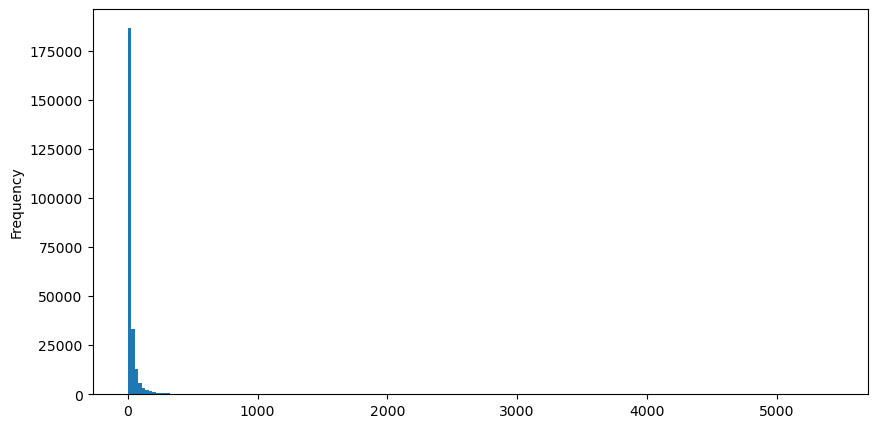
Prenons l’exemple des ordres d’achat, dessinons d’abord un histogramme. Vous pouvez voir que l’effet de longue traîne est très évident. La plupart des données sont concentrées à l’extrême gauche, mais il existe également un petit nombre de transactions importantes réparties à la queue .
buy_trades['quantity'].plot.hist(bins=200,figsize=(10, 5));
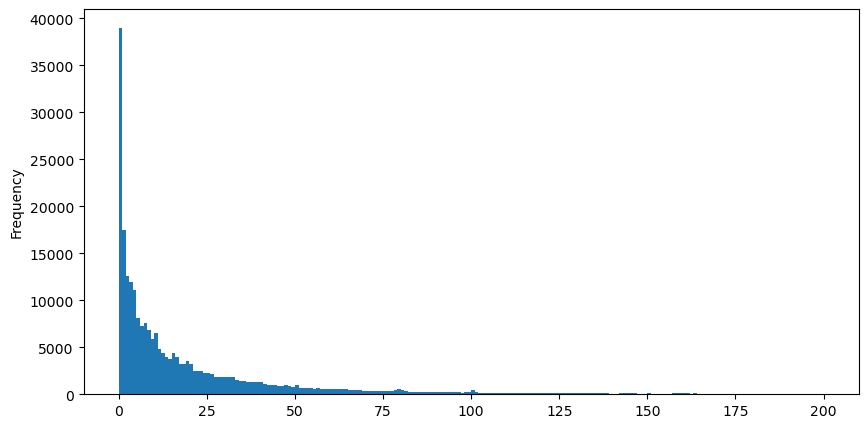
Pour faciliter l’observation, nous avons coupé la queue et observé. Nous pouvons voir que plus le volume d’échange est important, plus la fréquence d’occurrence est faible et plus la tendance à la baisse est rapide.
buy_trades['quantity'][buy_trades['quantity']<200].plot.hist(bins=200,figsize=(10, 5));
Il existe de nombreuses études sur la distribution de la satisfaction en volume. Sa distribution de puissance est également appelée distribution de Pareto, qui est une forme courante de distribution de probabilité en physique statistique et en sciences sociales. Dans une distribution de loi de puissance, la probabilité d’un événement d’une certaine taille (ou fréquence) est proportionnelle à un exposant négatif de la taille de cet événement. La principale caractéristique de cette forme de distribution est que les événements importants (c’est-à-dire ceux qui sont éloignés de la moyenne) se produisent plus fréquemment que ce à quoi on pourrait s’attendre dans de nombreuses autres distributions. C’est la caractéristique de la distribution du volume des échanges. La forme de la distribution de Pareto est : P(x) = Cx^(-α). Ce qui suit le démontrera.
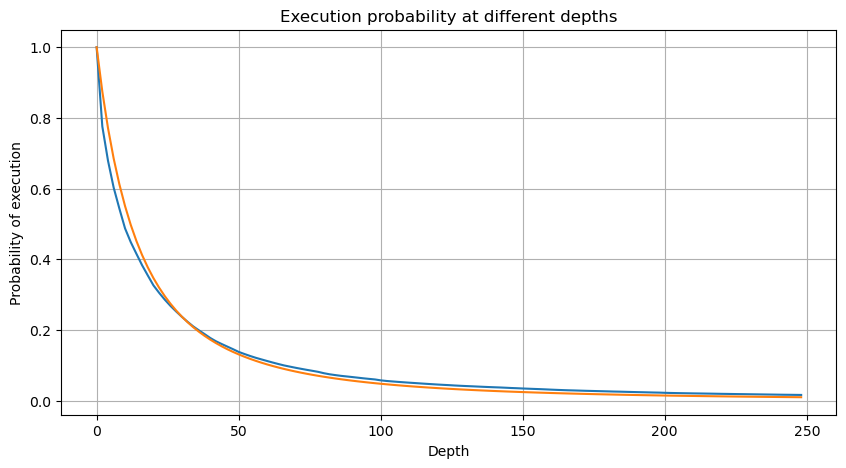
La figure ci-dessous montre la probabilité que le volume de transactions soit supérieur à une certaine valeur. La ligne bleue est la probabilité réelle et la ligne orange est la probabilité simulée. Ne vous inquiétez pas des paramètres spécifiques ici. Vous pouvez voir que cela ne se produit pas satisfaire la distribution de Pareto. Étant donné que la probabilité que le volume de la commande soit supérieur à 0 est de 1, et afin de répondre aux exigences de normalisation, l’équation de distribution doit être la suivante :
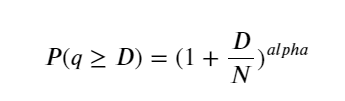
Où N est le paramètre standardisé. Ici, nous sélectionnons le volume moyen M et alpha -2,06. L’estimation spécifique de l’alpha peut être calculée en calculant inversement la valeur P lorsque D=N. Plus précisément : alpha = log(P(d>M))/log(2) . Le choix de points différents entraînera des valeurs alpha légèrement différentes.
depths = range(0, 250, 2)
probabilities = np.array([np.mean(buy_trades['quantity'] > depth) for depth in depths])
alpha = np.log(np.mean(buy_trades['quantity'] > mean_quantity))/np.log(2)
mean_quantity = buy_trades['quantity'].mean()
probabilities_s = np.array([(1+depth/mean_quantity)**alpha for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities)
plt.plot(depths, probabilities_s)
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.grid(True)
plt.figure(figsize=(10, 5))
plt.grid(True)
plt.title('Diff')
plt.plot(depths, probabilities_s-probabilities);
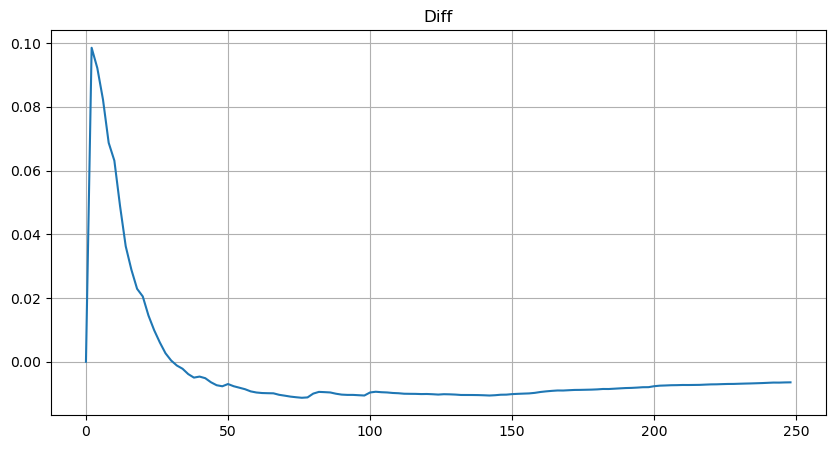
Mais cette estimation n’est qu’une apparence. Dans la figure ci-dessus, nous traçons la différence entre la valeur simulée et la valeur réelle. Lorsque le volume des échanges est faible, l’écart est important, voire proche de 10 %. La probabilité d’un point peut être rendue plus précise en sélectionnant différents points lors de l’estimation des paramètres, mais cela ne résout pas le problème de l’écart. Cela est déterminé par la différence entre la distribution de puissance et la distribution réelle. Afin d’obtenir des résultats plus précis, l’équation de la distribution de puissance doit être corrigée. Je n’entrerai pas dans les détails du processus spécifique, mais j’ai eu un éclair d’inspiration et j’ai découvert que cela devrait en fait être le suivant :
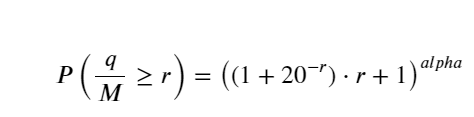
Pour plus de simplicité, r = q/M est utilisé ici pour représenter le volume de transactions standardisé. Les paramètres peuvent être estimés de la même manière que ci-dessus. La figure ci-dessous montre que l’écart maximal après correction ne dépasse pas 2 %. Théoriquement, la correction peut être poursuivie, mais cette précision est suffisante.
depths = range(0, 250, 2)
probabilities = np.array([np.mean(buy_trades['quantity'] > depth) for depth in depths])
mean = buy_trades['quantity'].mean()
alpha = np.log(np.mean(buy_trades['quantity'] > mean))/np.log(2.05)
probabilities_s = np.array([(((1+20**(-depth/mean))*depth+mean)/mean)**alpha for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities)
plt.plot(depths, probabilities_s)
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.grid(True)
plt.figure(figsize=(10, 5))
plt.grid(True)
plt.title('Diff')
plt.plot(depths, probabilities_s-probabilities);
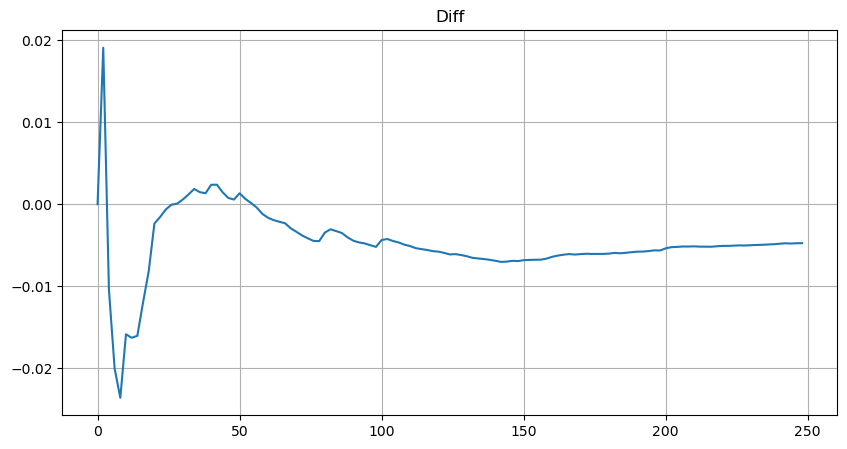
Avec l’équation estimée pour la distribution du volume, notez que la probabilité de l’équation n’est pas la vraie probabilité, mais une probabilité conditionnelle. À ce stade, nous pouvons répondre à cette question : si l’ordre suivant se produit, quelle est la probabilité que cet ordre soit supérieur à une certaine valeur ? En d’autres termes, quelle est la probabilité d’exécution d’ordres de différentes profondeurs (situation idéale, pas si rigoureuse, en théorie le carnet d’ordres comporte de nouveaux ordres et des annulations, ainsi que des files d’attente à la même profondeur).
L’article est presque terminé et il reste encore beaucoup de questions auxquelles il faut répondre. La série d’articles suivante tentera d’apporter des réponses.