Réflexions sur les stratégies de trading haute fréquence (3)
 0
0
 2664
2664

Dans l’article précédent, j’ai présenté comment modéliser le volume cumulé des transactions et j’ai brièvement analysé le phénomène de choc de prix. Cet article continuera d’analyser les données des commandes commerciales. Au cours des deux derniers jours, YGG a lancé des contrats basés sur Binance U, et le prix a beaucoup fluctué. Le volume des échanges a même dépassé le BTC à un moment donné. Analysons-le aujourd’hui.
Intervalle de temps de commande
En général, on suppose que le moment où les commandes arrivent suit un processus de Poisson. Voici un article qui présenteProcessus de Poisson . Je vais le démontrer ci-dessous.
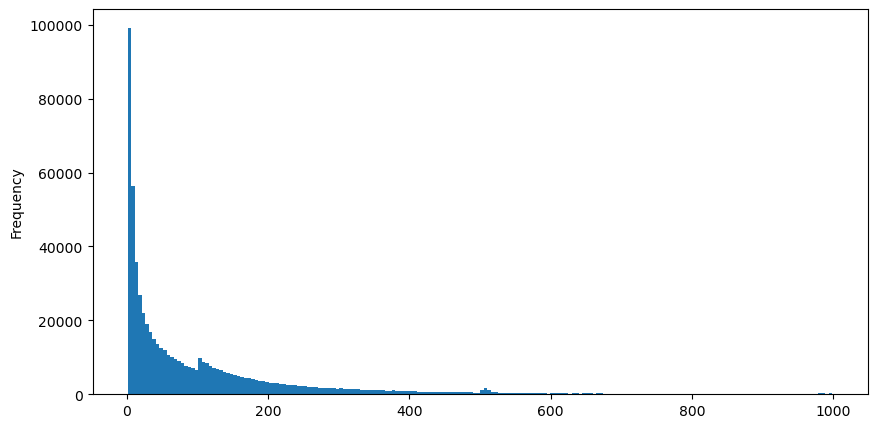
Téléchargez aggTrades le 5 août, il y a 1 931 193 transactions au total, ce qui est assez exagéré. Commençons par examiner la distribution des ordres d’achat. Nous pouvons constater qu’il existe un pic local irrégulier autour de 100 ms et 500 ms. Cela devrait être dû aux ordres programmés passés par le robot confié par Iceberg. Cela peut également être l’un des des raisons pour lesquelles les conditions du marché ce jour-là étaient inhabituelles.
La fonction de masse de probabilité (PMF) de la distribution de Poisson est donnée par :
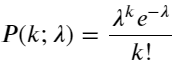
dans:
- k est le nombre d’événements qui nous intéressent.
- λ est le taux moyen d’occurrence des événements par unité de temps (ou unité d’espace).
- P(k; λ) est la probabilité que exactement k événements se produisent, étant donné un taux d’occurrence moyen λ.
Dans un processus de Poisson, les intervalles de temps entre les événements suivent une distribution exponentielle. La fonction de densité de probabilité (PDF) de la distribution exponentielle est donnée par :
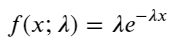
L’ajustement a permis de constater que les résultats étaient très différents des résultats attendus de la distribution de Poisson. Le processus de Poisson sous-estimait la fréquence des intervalles longs et surestimait la fréquence des intervalles courts. (La distribution d’intervalle réelle est plus proche de la distribution de Pareto modifiée)
from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
trades = pd.read_csv('YGGUSDT-aggTrades-2023-08-05.csv')
trades['date'] = pd.to_datetime(trades['transact_time'], unit='ms')
trades.index = trades['date']
buy_trades = trades[trades['is_buyer_maker']==False].copy()
buy_trades = buy_trades.groupby('transact_time').agg({
'agg_trade_id': 'last',
'price': 'last',
'quantity': 'sum',
'first_trade_id': 'first',
'last_trade_id': 'last',
'is_buyer_maker': 'last',
'date': 'last',
'transact_time':'last'
})
buy_trades['interval']=buy_trades['transact_time'] - buy_trades['transact_time'].shift()
buy_trades.index = buy_trades['date']
buy_trades['interval'][buy_trades['interval']<1000].plot.hist(bins=200,figsize=(10, 5));
Intervals = np.array(range(0, 1000, 5))
mean_intervals = buy_trades['interval'].mean()
buy_rates = 1000/mean_intervals
probabilities = np.array([np.mean(buy_trades['interval'] > interval) for interval in Intervals])
probabilities_s = np.array([np.e**(-buy_rates*interval/1000) for interval in Intervals])
plt.figure(figsize=(10, 5))
plt.plot(Intervals, probabilities)
plt.plot(Intervals, probabilities_s)
plt.xlabel('Intervals')
plt.ylabel('Probability')
plt.grid(True)
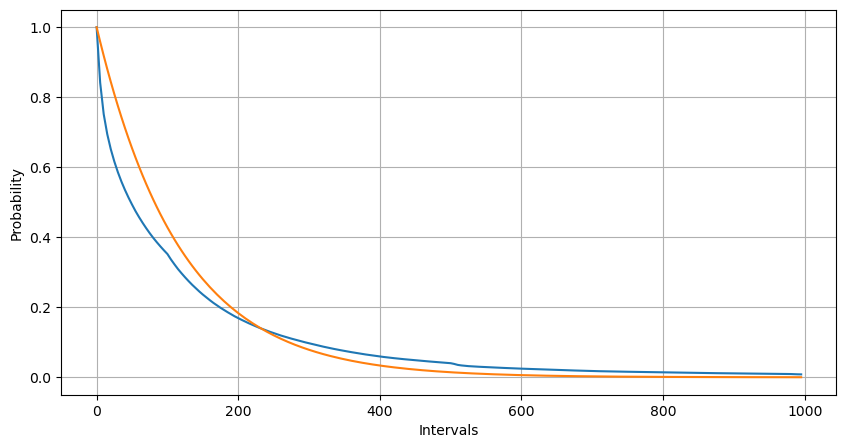
La distribution statistique du nombre de commandes qui se produisent en 1 seconde et la comparaison avec la distribution de Poisson montrent que la différence est également très évidente. La distribution de Poisson sous-estime considérablement la fréquence des événements à faible probabilité. Causes possibles :
- Taux d’occurrence non constant : le processus de Poisson suppose que le taux moyen d’événements se produisant au cours d’une période donnée est constant. Si cette hypothèse n’est pas vérifiée, la distribution des données s’écartera d’une distribution de Poisson.
- Interaction des processus : Une autre hypothèse de base du processus de Poisson est que les événements sont indépendants les uns des autres. Si les événements du monde réel s’influencent mutuellement, leur distribution peut s’écarter de la distribution de Poisson.
C’est-à-dire que dans un environnement réel, la fréquence des commandes n’est pas constante, doit être mise à jour en temps réel et des incitations se produiront, c’est-à-dire que plus de commandes dans un temps fixe stimuleront plus de commandes. Cela rend impossible la fixation d’un seul paramètre dans la stratégie.
result_df = buy_trades.resample('0.1S').agg({
'price': 'count',
'quantity': 'sum'
}).rename(columns={'price': 'order_count', 'quantity': 'quantity_sum'})
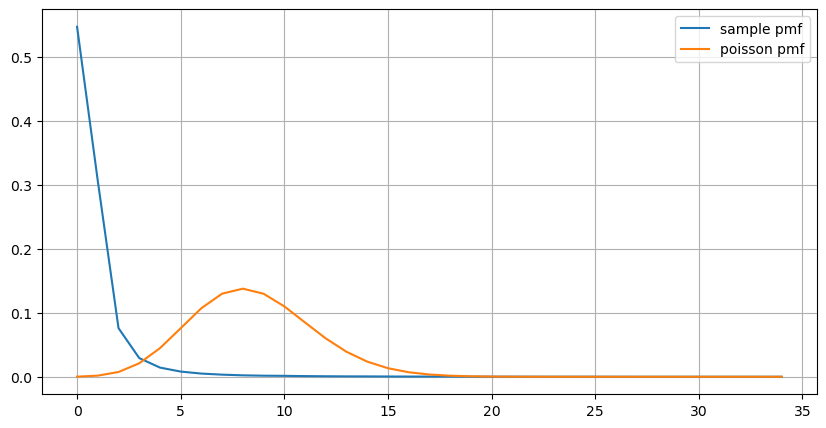
count_df = result_df['order_count'].value_counts().sort_index()[result_df['order_count'].value_counts()>20]
(count_df/count_df.sum()).plot(figsize=(10,5),grid=True,label='sample pmf');
from scipy.stats import poisson
prob_values = poisson.pmf(count_df.index, 1000/mean_intervals)
plt.plot(count_df.index, prob_values,label='poisson pmf');
plt.legend() ;
Paramètres de mise à jour en temps réel
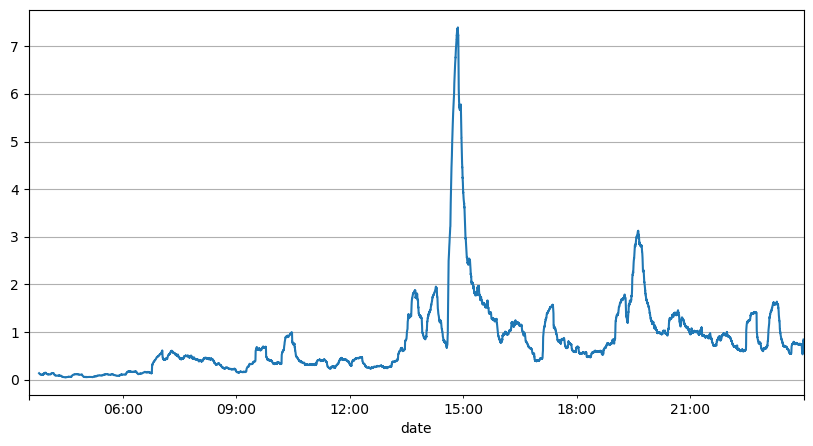
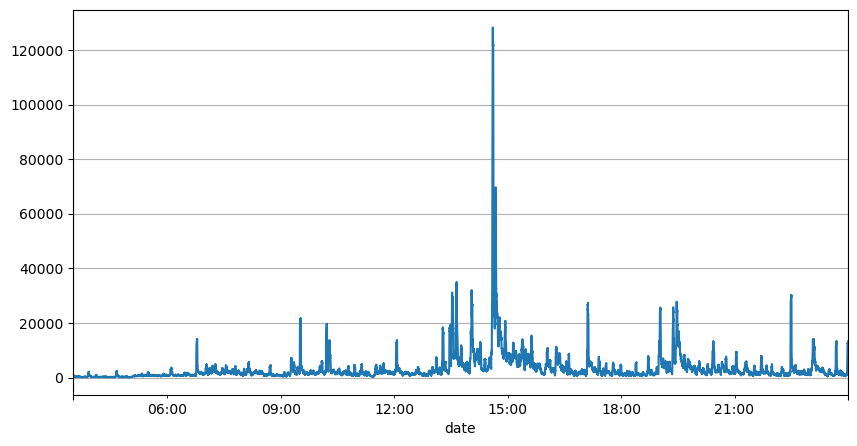
L’analyse précédente des intervalles de commande montre que les paramètres fixes ne sont pas adaptés aux conditions réelles du marché et que les paramètres clés de la description du marché de la stratégie doivent être mis à jour en temps réel. La solution la plus simple à laquelle penser est la moyenne mobile de la fenêtre glissante. Les deux chiffres ci-dessous représentent la fréquence des ordres d’achat en 1 seconde et la moyenne de 1000 fenêtres de volume de transactions. On peut constater qu’il existe un phénomène de regroupement dans les transactions, c’est-à-dire que la fréquence des ordres est nettement plus élevée que d’habitude pour un période de temps, et le volume à ce moment-là augmente également de manière synchrone. Ici, la moyenne précédente est utilisée pour prédire la valeur de la dernière seconde, et l’erreur absolue moyenne du résidu est utilisée pour mesurer la qualité de la prédiction.
Le graphique nous permet également de comprendre pourquoi la fréquence des commandes s’écarte autant de la distribution de Poisson. Bien que le nombre moyen de commandes par seconde ne soit que de 8,5 fois, dans les cas extrêmes, le nombre moyen de commandes par seconde s’écarte considérablement.
On constate ici que l’utilisation de la moyenne des deux secondes précédentes pour prédire l’erreur résiduelle est la plus faible et est bien meilleure que le simple résultat de prédiction de la moyenne.
result_df['order_count'][::10].rolling(1000).mean().plot(figsize=(10,5),grid=True);
result_df
| order_count | quantity_sum | |
|---|---|---|
| 2023-08-05 03:30:06.100 | 1 | 76.0 |
| 2023-08-05 03:30:06.200 | 0 | 0.0 |
| 2023-08-05 03:30:06.300 | 0 | 0.0 |
| 2023-08-05 03:30:06.400 | 1 | 416.0 |
| 2023-08-05 03:30:06.500 | 0 | 0.0 |
| … | … | … |
| 2023-08-05 23:59:59.500 | 3 | 9238.0 |
| 2023-08-05 23:59:59.600 | 0 | 0.0 |
| 2023-08-05 23:59:59.700 | 1 | 3981.0 |
| 2023-08-05 23:59:59.800 | 0 | 0.0 |
| 2023-08-05 23:59:59.900 | 2 | 534.0 |
result_df['quantity_sum'].rolling(1000).mean().plot(figsize=(10,5),grid=True);
(result_df['order_count'] - result_df['mean_count'].mean()).abs().mean()
6.985628185332997
result_df['mean_count'] = result_df['order_count'].ewm(alpha=0.11, adjust=False).mean()
(result_df['order_count'] - result_df['mean_count'].shift()).abs().mean()
0.6727616961866929
result_df['mean_quantity'] = result_df['quantity_sum'].ewm(alpha=0.1, adjust=False).mean()
(result_df['quantity_sum'] - result_df['mean_quantity'].shift()).abs().mean()
4180.171479076811
Résumer
Cet article présente brièvement les raisons pour lesquelles l’intervalle de temps d’ordre s’écarte du processus de Poisson, principalement parce que les paramètres changent au fil du temps. Afin de prédire le marché avec plus de précision, la stratégie doit faire des prédictions en temps réel sur les paramètres de base du marché. Les résidus peuvent être utilisés pour mesurer la qualité des prévisions. L’exemple ci-dessus est le plus simple. Il existe de nombreuses études connexes sur l’analyse des séries chronologiques, l’agrégation de la volatilité, etc., qui peuvent encore être améliorées.