L’article précédent a étudié l’intervalle d’arrivée des commandes et a démontré pourquoi nous devons ajuster dynamiquement les paramètres et comment évaluer la qualité de l’estimation. Cet article se concentrera sur des données approfondies et étudiera le prix moyen (également appelé prix équitable, micro-prix, etc.).

Données de profondeur

Binance fournit un téléchargement de données historiques des meilleures cotations, notamment best_bid_price : le meilleur prix d’offre, c’est-à-dire le prix d’offre maximum, best_bid_qty : le numéro du meilleur prix d’offre, best_ask_price : le meilleur prix de vente, best_ask_qty : le numéro du meilleur prix de vente , transaction_time : horodatage. Ces données n’incluent pas les commandes en attente de deuxième niveau et plus profondes. La situation du marché analysée ici est celle de YGG le 7 août. Les fluctuations du marché ce jour-là ont été très drastiques et la quantité de données a atteint plus de 9 millions.

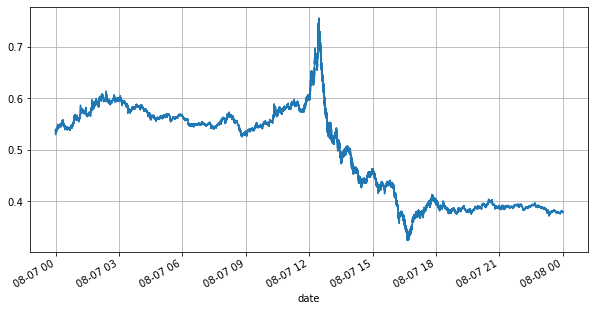
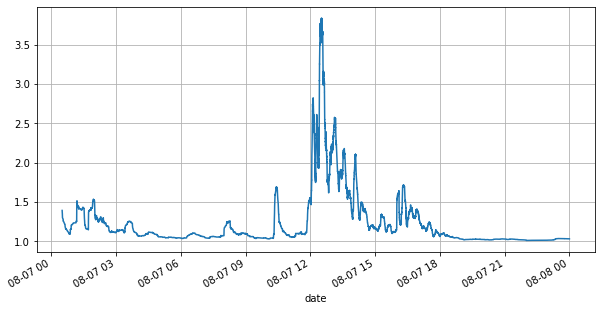
Tout d’abord, regardons le marché du jour. Il connaît de grands hauts et des bas. De plus, le nombre d’ordres en attente sur la journée a également beaucoup changé avec la fluctuation du marché. En particulier, le spread (la différence entre le (prix de vente et prix d’achat) a montré de manière significative la situation de fluctuation du marché. Selon les statistiques du marché de YGG ce jour-là, 20 % du temps, le spread était supérieur à 1 tick. À l’ère où différents robots se font concurrence sur le marché, cette situation est rare.

from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

books = pd.read_csv('YGGUSDT-bookTicker-2023-08-07.csv')

tick_size = 0.0001

books['date'] = pd.to_datetime(books['transaction_time'], unit='ms')
books.index = books['date']

books['spread'] = round(books['best_ask_price'] - books['best_bid_price'],4)

books['best_bid_price'][::10].plot(figsize=(10,5),grid=True);

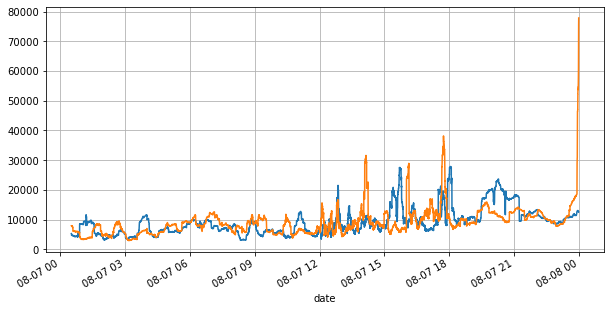
books['best_bid_qty'][::10].rolling(10000).mean().plot(figsize=(10,5),grid=True);
books['best_ask_qty'][::10].rolling(10000).mean().plot(figsize=(10,5),grid=True);

(books['spread'][::10]/tick_size).rolling(10000).mean().plot(figsize=(10,5),grid=True);

books['spread'].value_counts()[books['spread'].value_counts()>500]/books['spread'].value_counts().sum()

0.0001    0.799169
0.0002    0.102750
0.0003    0.042472
0.0004    0.022821
0.0005    0.012792
0.0006    0.007350
0.0007    0.004376
0.0008    0.002712
0.0009    0.001657
0.0010    0.001089
0.0011    0.000740
0.0012    0.000496
0.0013    0.000380
0.0014    0.000258
0.0015    0.000197
0.0016    0.000140
0.0017    0.000112
0.0018    0.000088
0.0019    0.000063
Name: spread, dtype: float64

Citations déséquilibrées

Comme on peut le voir ci-dessus, les volumes des ordres d’achat et de vente sont très différents la plupart du temps. Cette différence a un effet prédictif important sur les conditions de marché à court terme. La raison est similaire à celle mentionnée dans l’article précédent selon laquelle les petits ordres d’achat entraînent souvent des baisses. Si les ordres en attente d’un côté sont nettement plus petits que ceux de l’autre côté, et en supposant que les volumes d’ordres d’achat et de vente actifs sont proches, le côté avec les ordres en attente les plus petits sera plus susceptible d’être absorbé, ce qui entraînera une hausse des prix. changements. Les citations déséquilibrées sont représentées par I : 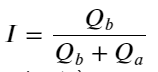Où Q_b représente la quantité de l’ordre d’achat (best_bid_qty) et Q_a représente la quantité de l’ordre de vente (best_ask_qty).

Définir le prix moyen :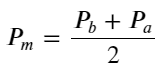

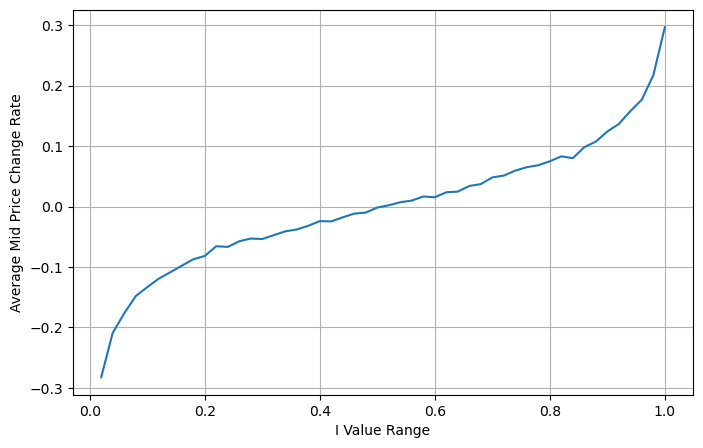
La figure suivante montre la relation entre le taux de variation du prix moyen dans l’intervalle suivant et le déséquilibre I. Comme prévu, à mesure que I augmente, le prix est plus susceptible d’augmenter et plus il est proche de 1, plus l’ampleur du déséquilibre est élevée. Le changement de prix s’accélère également. Dans le trading haute fréquence, l’introduction du prix moyen a pour but de mieux prédire les évolutions futures des prix. En d’autres termes, plus la différence par rapport au prix futur est faible, mieux le prix moyen est défini. De toute évidence, le déséquilibre des ordres en attente fournit des informations supplémentaires pour la prédiction de la stratégie. En tenant compte de cela, nous définissons le prix moyen pondéré :

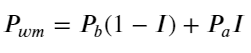
books['I'] = books['best_bid_qty'] / (books['best_bid_qty'] + books['best_ask_qty'])

books['mid_price'] = (books['best_ask_price'] + books['best_bid_price'])/2

bins = np.linspace(0, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['price_change'] = (books['mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['price_change'].mean()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Average Mid Price Change Rate');
plt.grid(True)

books['weighted_mid_price'] = books['mid_price'] + books['spread']*books['I']/2
bins = np.linspace(-1, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['weighted_price_change'] = (books['weighted_mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['weighted_price_change'].mean()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Weighted Average Mid Price Change Rate');
plt.grid(True)

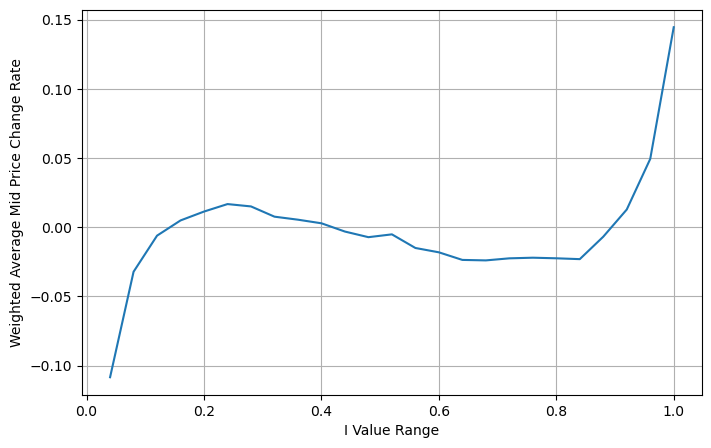
Ajuster le prix moyen pondéré

À partir de la figure, nous pouvons voir que la variation du prix moyen pondéré est beaucoup plus faible que celle des différents I, ce qui signifie que le prix moyen pondéré est un meilleur ajustement. Mais il existe encore quelques régularités, comme autour de 0,2 et 0,8, où les écarts sont importants. Cela montre que je peux encore apporter des informations supplémentaires. Étant donné que le prix moyen pondéré suppose que le terme de correction du prix est complètement linéaire avec I, cela n’est évidemment pas vrai. Comme on peut le voir sur la figure ci-dessus, lorsque I est proche de 0 et 1, l’écart est plus rapide et il ne s’agit pas d’un relation linéaire.

Pour un look plus intuitif, je suis redéfini ici :

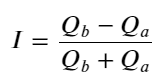
à ce moment-là:

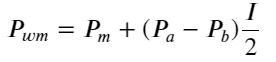
En observant cette forme, nous pouvons constater que le prix moyen pondéré est une correction du prix moyen moyen. Le coefficient du terme de correction est Spread, et le terme de correction est une fonction de I. Le prix moyen pondéré suppose simplement que cette relation est I/2. À ce stade, l’avantage de la distribution ajustée de I (-1,1) se reflète. I est symétrique par rapport à l’origine, ce qui nous permet de trouver facilement la relation d’ajustement de la fonction. Observez le graphique, cette fonction devrait satisfaire la relation de puissance impaire de I, ce qui est cohérent avec la croissance rapide des deux côtés et la symétrie par rapport à l’origine. De plus, on peut observer que la valeur proche de l’origine est proche de la linéarité, et quand I est 0, le résultat de la fonction est 0, et quand I est 1, le résultat de la fonction est 0,5. Alors, je suppose que cette fonction ressemble à :

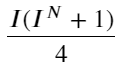
Ici, N est un nombre pair positif. Après des tests réels, il est préférable que N soit égal à 8. Jusqu’à présent, cet article propose un prix moyen pondéré révisé :

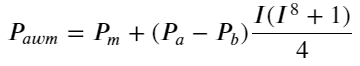
À ce stade, le changement du prix moyen prévu n’a pratiquement rien à voir avec moi. Bien que ce résultat soit meilleur que le simple prix moyen pondéré, il ne peut pas être appliqué dans le cadre de transactions réelles. Il s’agit simplement d’une idée donnée ici. Un article de 2017 de S Stoikov a présenté la méthode de la chaîne de MarkovMicro-Price, et donne le code pertinent, vous pouvez également l’étudier.

books['I'] = (books['best_bid_qty'] - books['best_ask_qty']) / (books['best_bid_qty'] + books['best_ask_qty'])

books['weighted_mid_price'] = books['mid_price'] + books['spread']*books['I']/2
bins = np.linspace(-1, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['weighted_price_change'] = (books['weighted_mid_price'].pct_change()/tick_size).shift(-1)
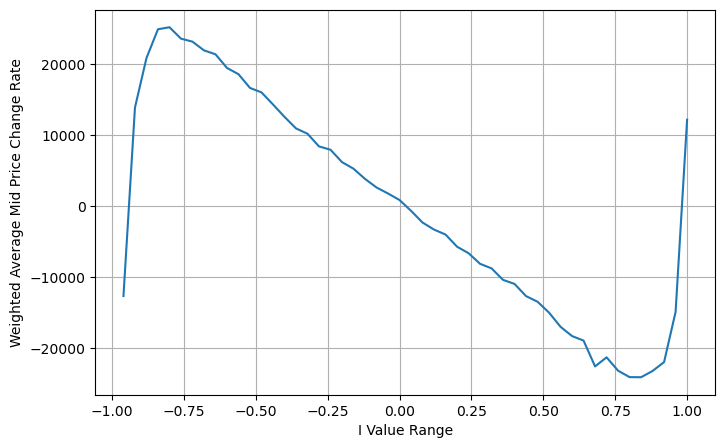
avg_change = books.groupby('I_bins')['weighted_price_change'].sum()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Weighted Average Mid Price Change Rate');
plt.grid(True)

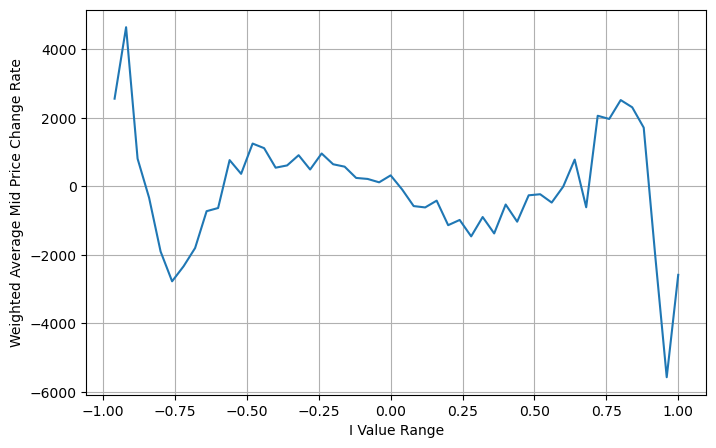
books['adjust_mid_price'] = books['mid_price'] + books['spread']*(books['I'])*(books['I']**8+1)/4
bins = np.linspace(-1, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['adjust_mid_price'] = (books['adjust_mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['adjust_mid_price'].sum()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Weighted Average Mid Price Change Rate');
plt.grid(True)

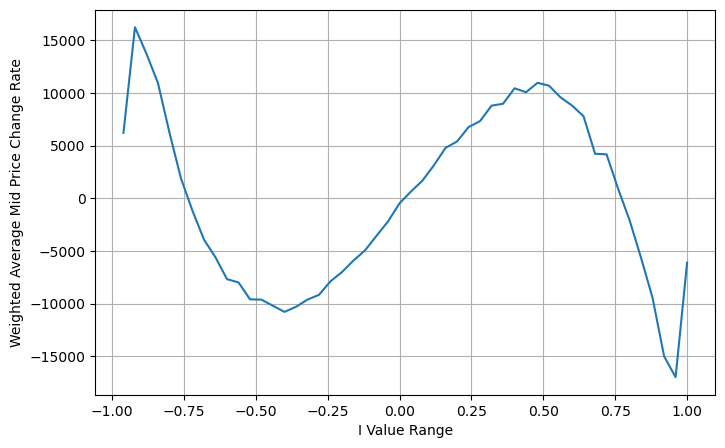
books['adjust_mid_price'] = books['mid_price'] + books['spread']*(books['I']**3)/2
bins = np.linspace(-1, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['adjust_mid_price'] = (books['adjust_mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['adjust_mid_price'].sum()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Weighted Average Mid Price Change Rate');
plt.grid(True)

Résumer

Le prix moyen est très important pour les stratégies à haute fréquence. Il s’agit d’une prévision des prix futurs à court terme, le prix moyen doit donc être aussi précis que possible. Les prix moyens introduits ci-dessus sont tous basés sur des données de marché, car un seul prix de marché est utilisé dans l’analyse. Dans le trading réel, la stratégie doit utiliser autant que possible toutes les données, en particulier lorsqu’il y a des échanges de transactions dans le trading réel, et la prédiction du prix moyen doit être testée par le prix de transaction réel. Je me souviens que Stoikov semblait avoir posté un tweet disant que le prix moyen réel devrait être la moyenne pondérée de la probabilité d’une transaction d’achat-vente. Cette question vient d’être étudiée dans l’article précédent. En raison de l’espace limité, ces questions seront abordées en détail dans le prochain article.