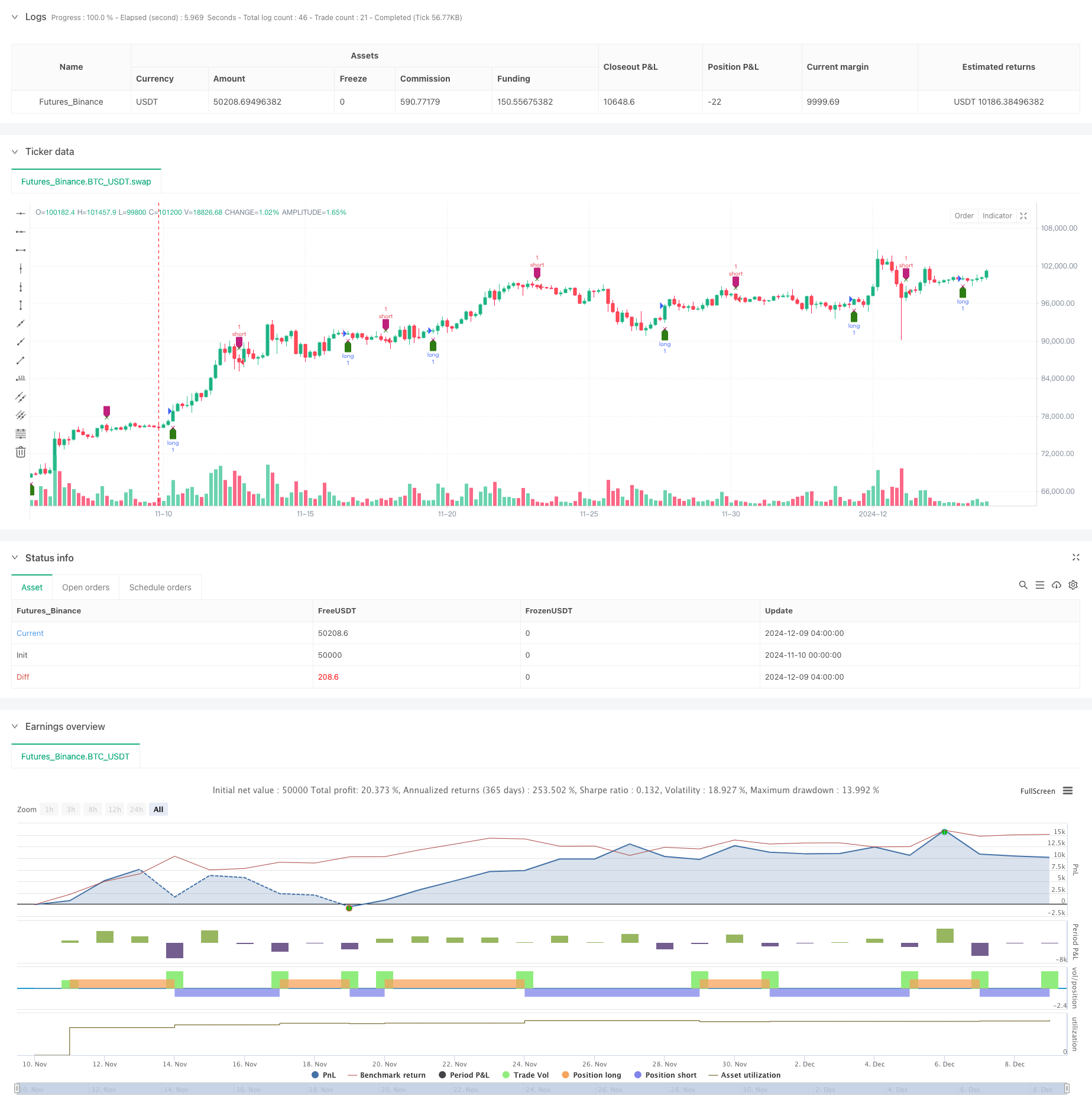
La stratégie est un système de trading quantitatif basé sur un oscillateur dynamique RSI. La stratégie utilise des méthodes mathématiques avancées telles que la décomposition de QR pour le traitement des signaux et la prise de décision de négociation en combinaison avec un système linéaire uniforme.

Principe de stratégie

Le cœur de la stratégie est l'oscillateur Delta-RSI, qui se réalise par les étapes suivantes:

1. Comptez d'abord le RSI traditionnel comme base de données.
2. Le RSI est traité en douceur par l'adaptation polynomial, ce qui réduit le bruit
3. Calculer le coefficient de temps du RSI obtenu par Delta-RSI, qui reflète le taux de variation du RSI
4. Générer des signaux de trading en comparant le Delta-RSI avec sa moyenne mobile
5. Évaluation et filtrage de la qualité d'adaptation à l'aide de l'erreur de racine carrée uniforme (RMSE)

Les signaux de transaction peuvent être générés de trois façons:

• Traversage de la ligne zéro: Delta-RSI est plus quand il est positif et négatif quand il est négatif
• La ligne de signal se croise: le Delta-RSI est en hausse / en baisse de sa moyenne mobile, faisant respectivement plus / moins
• Changement de direction: le delta-RSI fait plus lorsque la zone négative commence à monter et fait moins lorsque la zone positive commence à baisser

Avantages stratégiques

1. Les bases mathématiques sont solides: le traitement des signaux est effectué par des méthodes mathématiques avancées telles que la décomposition de la résolution de QR, et les bases théoriques sont solides.
2. Signal de lissage: la combinaison de plusieurs paramètres peut filtrer efficacement le bruit du marché et améliorer la qualité du signal
3. Flexibilité: offre une variété de modes de génération de signaux et de choix de paramètres pour s'adapter à différents environnements de marché
4. Risque maîtrisé: un mécanisme de filtrage RMSE est inclus pour filtrer les signaux les plus fiables
5. Calcul efficace: les opérations matricielles utilisent des algorithmes optimisés et fonctionnent de manière plus efficace

Risque stratégique

1. Sensitivité des paramètres: plusieurs paramètres clés nécessitent un ajustement minutieux et une mauvaise sélection de paramètres peut avoir un impact négatif sur la performance de la stratégie
2. La latence: un traitement de signal en douceur entraîne un certain retard et peut manquer une action rapide.
3. Fausse rupture: risque de faux signaux et de coûts de transaction dans un marché en crise
4. Calcul complexe: impliquant plus d'opérations matricielles, il peut y avoir des blocages de performance dans les transactions à haute fréquence
5. Surmesure: attention à ne pas surmesurer les données historiques lors de l'optimisation des paramètres

Orientation de l'optimisation de la stratégie

1. Paramètres d'adaptation: le RSI peut être ajusté en fonction de la dynamique des fluctuations du marché
2. Périodes de temps multiples: les signaux associés à des périodes de temps multiples sont vérifiés par croisement
3. Filtrage de la fréquence d'oscillation: ajout d'indicateurs de fréquence d'oscillation tels que l'ATR pour filtrer le signal
4. Classification des marchés: différentes règles de génération de signaux sont utilisées pour différents états du marché (trends / oscillations)
5. Optimisation des arrêts de perte: ajout de mécanismes d'arrêt plus intelligents, tels que des arrêts de perte dynamiques basés sur des points de résistance de soutien

Résumer

Il s'agit d'une stratégie de trading quantitatif structurée et solide en théorie. Grâce à l'analyse des caractéristiques dynamiques du RSI, le traitement des signaux en combinaison avec des méthodes mathématiques modernes, il est possible de mieux capturer les tendances du marché. Bien qu'il existe une certaine sensibilité aux paramètres et des problèmes de complexité de calcul, la stratégie a une bonne valeur d'application grâce à une sélection et à une optimisation rationnelles des paramètres. Il est recommandé de prêter attention au contrôle des risques lors de l'application en direct, de définir raisonnablement les positions et de surveiller en permanence la performance de la stratégie.